Main Effects Plot for a Row-Column Interaction Model (RCIM)

Produces a main effects plot for Row-Column Interaction Models (RCIMs).

plotrcim0(object, centered = TRUE, which.plots = c(1, 2),
            hline0 = TRUE, hlty = "dashed", hcol = par()$col, hlwd = par()$lwd,
            rfirst = 1, cfirst = 1,
            rtype = "h", ctype = "h",
            rcex.lab = 1, rcex.axis = 1, rtick = FALSE,
            ccex.lab = 1, ccex.axis = 1, ctick = FALSE,
            rmain = "Row effects", rsub = "",
            rxlab = "", rylab = "Row effects",
            cmain = "Column effects", csub = "",
            cxlab= "", cylab = "Column effects",
            rcol = par()$col, ccol = par()$col,
            no.warning = FALSE, ...)

Arguments

object

An rcim object. This should be of rank-0, i.e., main effects only and no interactions.

which.plots

Numeric, describing which plots are to be plotted. The row effects plot is 1 and the column effects plot is 2. Set the value 0, say, for no plots at all.

centered

Logical. If TRUE then the row and column effects are centered (but not scaled) by scale. If FALSE then the raw effects are used (of which the first are zero by definition).

hline0, hlty, hcol, hlwd

hline0 is logical. If TRUE then a horizontal line is plotted at 0 and the other arguments describe this line. Probably having hline0 = TRUE only makes sense when centered = TRUE.

rfirst, cfirst

rfirst is the level of row that is placed first in the row effects plot, etc.

rmain, cmain

Character. rmain is the main label in the row effects plot, etc.

rtype, ctype, rsub, csub

See the type and sub arguments of plot.default.

rxlab, rylab, cxlab, cylab

Character. For the row effects plot, rxlab is xlab and rylab is ylab; see par. Ditto for cxlab and cylab for the column effects plot.

rcex.lab, ccex.lab

Numeric. rcex.lab is cex for the row effects plot label, etc.

rcex.axis, ccex.axis

Numeric. rcex.axis is the cex argument for the row effects axis label, etc.

rtick, ctick

Logical. If rtick = TRUE then add ticks to the row effects plot, etc.

rcol, ccol

rcol give a colour for the row effects plot, etc.

no.warning

Logical. If TRUE then no warning is issued if the model is not rank-0.

...

Arguments fed into plot.default, etc.

Details

This function plots the row and column effects of a rank-0 RCIM. As the result is a main effects plot of a regression analysis, its interpretation when centered = FALSE is relative to the baseline (reference level) of a row and column, and should also be considered in light of the link function used. Many arguments that start with "r" refer to the row effects plot, and "c" for the column effects plot.

Value

The original object with the post slot assigned additional information from the plot.

Note

This function should be only used to plot the object of rank-0 RCIM. If the rank is positive then it will issue a warning.

Using an argument ylim will mean the row and column effects are plotted on a common scale; see plot.window.

Author

T. W. Yee, A. F. Hadi.

See also

moffset Rcim, rcim.

Examples

alcoff.e <- moffset(alcoff, "6", "Mon", postfix = "*")  # Effective day
fit0 <- rcim(alcoff.e, family = poissonff)
if (FALSE) par(oma = c(0, 0, 4, 0), mfrow = 1:2)  # For all plots below too
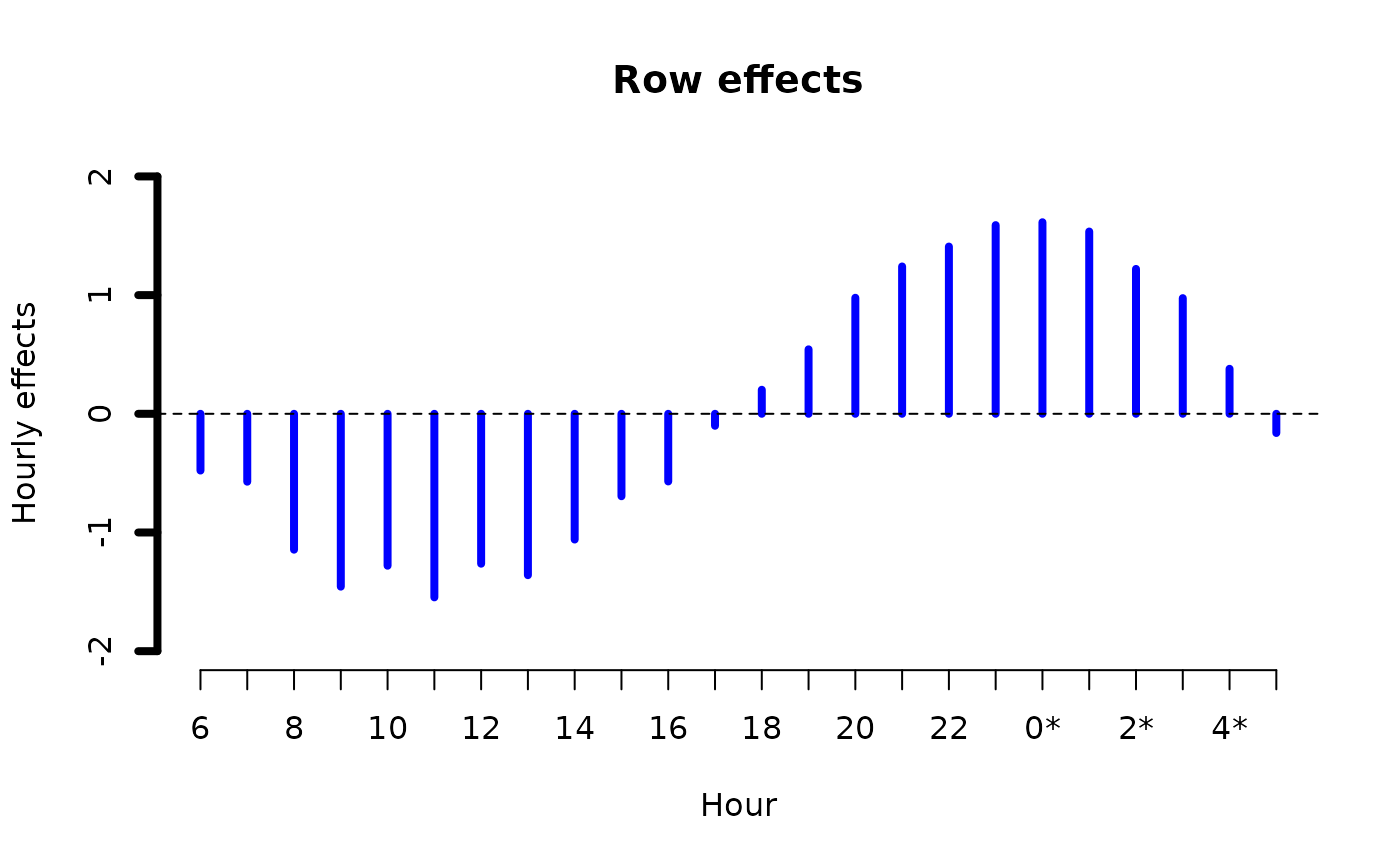
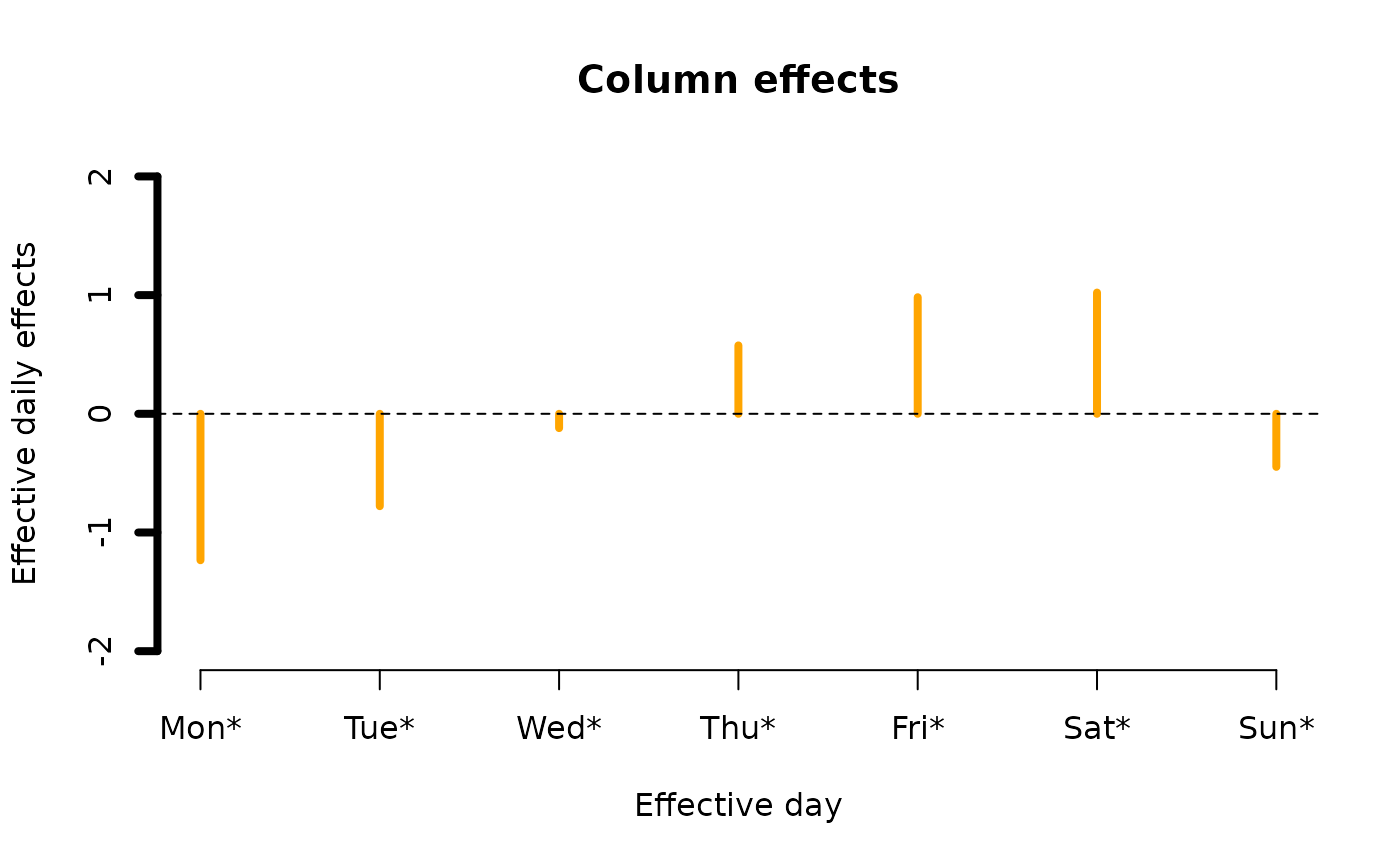
ii <- plot(fit0, rcol = "blue", ccol = "orange",
           lwd = 4, ylim = c(-2, 2),  # A common ylim
           cylab = "Effective daily effects", rylab = "Hourly effects",
           rxlab = "Hour", cxlab = "Effective day")


ii@post  # Endowed with additional information
#> $row.effects
#>              [,1]
#> Row.1  -0.4781335
#> Row.2  -0.5721087
#> Row.3  -1.1449138
#> Row.4  -1.4564215
#> Row.5  -1.2800397
#> Row.6  -1.5466684
#> Row.7  -1.2631617
#> Row.8  -1.3597279
#> Row.9  -1.0594526
#> Row.10 -0.6946199
#> Row.11 -0.5700145
#> Row.12 -0.1010574
#> Row.13  0.2025315
#> Row.14  0.5431360
#> Row.15  0.9777261
#> Row.16  1.2414246
#> Row.17  1.4091096
#> Row.18  1.5897916
#> Row.19  1.6141074
#> Row.20  1.5357512
#> Row.21  1.2206984
#> Row.22  0.9746059
#> Row.23  0.3792010
#> Row.24 -0.1617638
#> attr(,"scaled:center")
#> [1] 0.4781335
#> 
#> $col.effects
#>             [,1]
#> Col.1 -1.2338194
#> Col.2 -0.7783439
#> Col.3 -0.1206174
#> Col.4  0.5762210
#> Col.5  0.9822999
#> Col.6  1.0214144
#> Col.7 -0.4471546
#> attr(,"scaled:center")
#> [1] 1.233819
#> 
#> $raw.row.effects
#>       Row.1       Row.2       Row.3       Row.4       Row.5       Row.6 
#>  0.00000000 -0.09397519 -0.66678030 -0.97828796 -0.80190617 -1.06853483 
#>       Row.7       Row.8       Row.9      Row.10      Row.11      Row.12 
#> -0.78502813 -0.88159433 -0.58131908 -0.21648637 -0.09188095  0.37707610 
#>      Row.13      Row.14      Row.15      Row.16      Row.17      Row.18 
#>  0.68066502  1.02126950  1.45585959  1.71955808  1.88724312  2.06792510 
#>      Row.19      Row.20      Row.21      Row.22      Row.23      Row.24 
#>  2.09224096  2.01388469  1.69883194  1.45273946  0.85733456  0.31636967 
#> 
#> $raw.col.effects
#>     Col.1     Col.2     Col.3     Col.4     Col.5     Col.6     Col.7 
#> 0.0000000 0.4554755 1.1132020 1.8100404 2.2161194 2.2552339 0.7866649 
#> 
 # \dontrun{}

# Negative binomial example
if (FALSE) { # \dontrun{
fit1 <- rcim(alcoff.e, negbinomial, trace = TRUE)
plot(fit1, ylim = c(-2, 2)) } # }

# Univariate normal example
fit2 <- rcim(alcoff.e, uninormal, trace = TRUE)
#> Iteration 1: loglikelihood = -1232.2968
#> Iteration 2: loglikelihood = -1168.6442
#> Iteration 3: loglikelihood = -1128.0555
#> Iteration 4: loglikelihood = -1114.4362
#> Iteration 5: loglikelihood = -1113.2052
#> Iteration 6: loglikelihood = -1113.1961
#> Iteration 7: loglikelihood = -1113.1961
if (FALSE)  plot(fit2, ylim = c(-200, 400))  # \dontrun{}

# Median-polish example
if (FALSE) { # \dontrun{
fit3 <- rcim(alcoff.e, alaplace1(tau = 0.5), maxit = 1000, trace = FALSE)
plot(fit3, ylim = c(-200, 250)) } # }

# Zero-inflated Poisson example on "crashp" (no 0s in alcoff)
if (FALSE) { # \dontrun{
cbind(rowSums(crashp))  # Easy to see the data
cbind(colSums(crashp))  # Easy to see the data
fit4 <- rcim(Rcim(crashp, rbaseline = "5", cbaseline = "Sun"),
             zipoissonff, trace = TRUE)
plot(fit4, ylim = c(-3, 3)) } # }