Trivariate Normal Distribution Density and Random Variates

Density and random generation for the trivariate normal distribution distribution.

dtrinorm(x1, x2, x3, mean1 = 0, mean2 = 0, mean3 = 0,
         var1 = 1, var2 = 1, var3 = 1,
         cov12 = 0, cov23 = 0, cov13 = 0, log = FALSE)
rtrinorm(n,          mean1 = 0, mean2 = 0, mean3 = 0,
         var1 = 1, var2 = 1, var3 = 1,
         cov12 = 0, cov23 = 0, cov13 = 0)

Arguments

x1, x2, x3

vector of quantiles.

mean1, mean2, mean3

vectors of means.

var1, var2, var3

vectors of variances.

cov12, cov23, cov13

vectors of covariances.

n

number of observations. Same as rnorm.

log

Logical. If log = TRUE then the logarithm of the density is returned.

Value

dtrinorm gives the density, rtrinorm generates random deviates (\(n\) by 3 matrix).

Details

The default arguments correspond to the standard trivariate normal distribution with correlation parameters equal to 0, which corresponds to three independent standard normal distributions. Let sd1 (say) be sqrt(var1) and written \(\sigma_1\), etc. Then the general formula for each correlation coefficient is of the form \(\rho_{12} = cov_{12} / (\sigma_1 \sigma_2)\), and similarly for the two others. Thus if the var arguments are left alone then the cov can be inputted with \(\rho\)s.

Warning

dtrinorm()'s arguments might change in the future! It's safest to use the full argument names to future-proof possible changes!

Note

For rtrinorm(), if the \(i\)th variance-covariance matrix is not positive-definite then the \(i\)th row is all NAs.

See also

pnorm, trinormal, uninormal, binormal, rbinorm.

Examples

if (FALSE) nn <- 1000
tdata <- data.frame(x2 = sort(runif(nn)))
tdata <- transform(tdata, mean1 = 1 + 2 * x2,
                   mean2 = 3 + 1 * x2, mean3 = 4,
                   var1 = exp( 1), var2 = exp( 1), var3 = exp( 1),
                   rho12 = rhobitlink( 1, inverse = TRUE),
                   rho23 = rhobitlink( 1, inverse = TRUE),
                   rho13 = rhobitlink(-1, inverse = TRUE))
ymat <- with(tdata, rtrinorm(nn, mean1, mean2, mean3,
                             var1, var2, var3,
                             sqrt(var1)*sqrt(var1)*rho12,
                             sqrt(var2)*sqrt(var3)*rho23,
                             sqrt(var1)*sqrt(var3)*rho13))
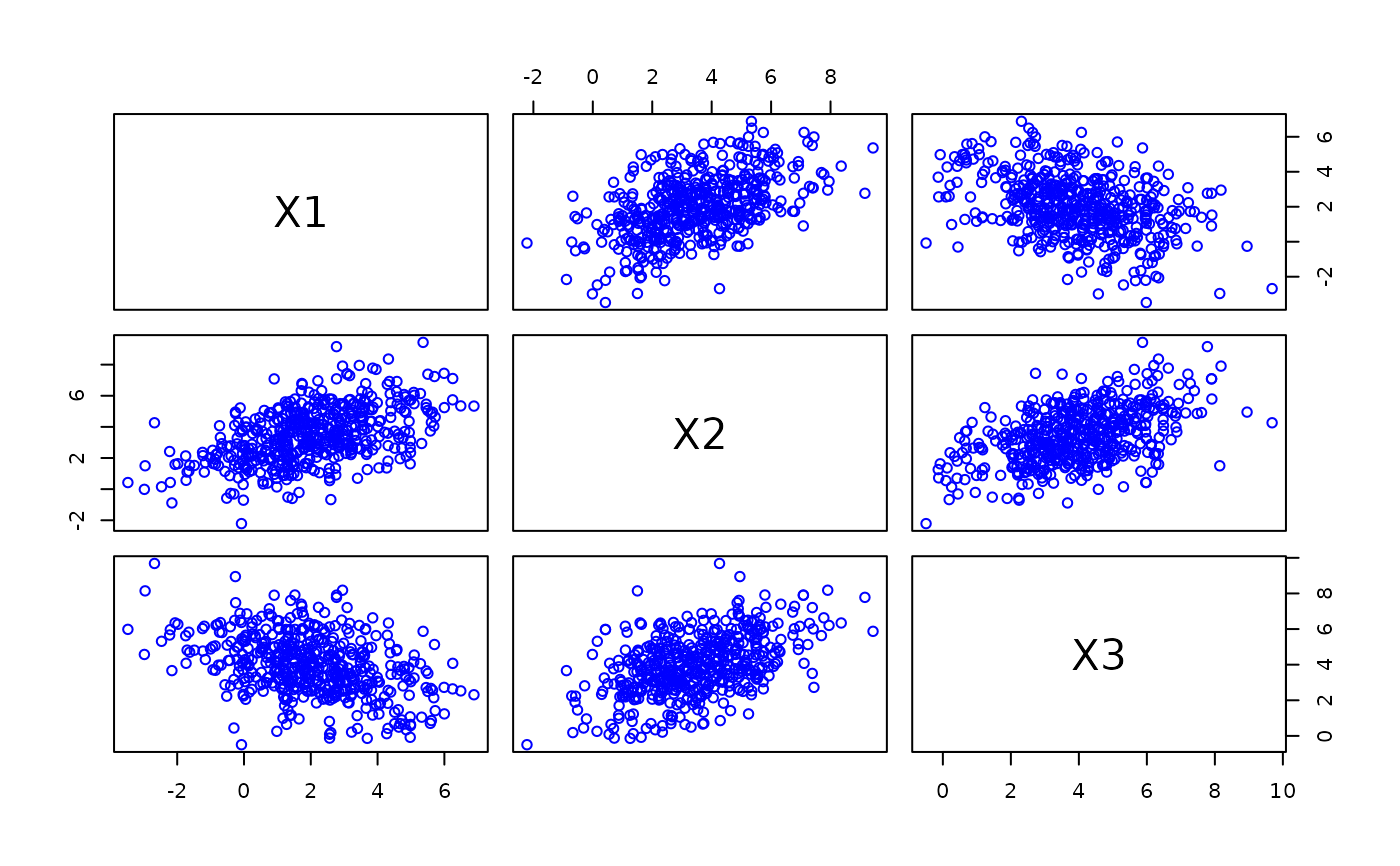
pairs(ymat, col = "blue")

 # \dontrun{}