Zero-Inflated Poisson Distribution

Density, distribution function, quantile function and random generation for the zero-inflated and zero-deflated Poisson distribution with parameter pstr0.

dzipois(x, lambda, pstr0 = 0, log = FALSE)
pzipois(q, lambda, pstr0 = 0)
qzipois(p, lambda, pstr0 = 0)
rzipois(n, lambda, pstr0 = 0)

Arguments

x, q

vector of quantiles.

p

vector of probabilities.

n

number of observations. Must be a single positive integer.

lambda

Vector of positive means.

pstr0

Probability of a structural zero (i.e., ignoring the Poisson distribution), called \(\phi\). The default value of \(\phi = 0\) corresponds to the response having an ordinary Poisson distribution. If \(\phi\) lies in (0, 1) then this is known as the zero-inflated Poisson (ZIP) distribution. This argument may be negative to allow for 0-deflation, hence its interpretation as a probability ceases.

log

Logical. Return the logarithm of the answer?

Details

The probability function of \(Y\) is 0 with probability \(\phi\), and \(Poisson(\lambda)\) with probability \(1-\phi\). Thus $$P(Y=0) =\phi + (1-\phi) P(W=0)$$ where \(W\) is distributed \(Poisson(\lambda)\).

Value

dzipois gives the density, pzipois gives the distribution function, qzipois gives the quantile function, and rzipois generates random deviates.

Author

T. W. Yee

Note

The argument pstr0 is recycled to the required length, and must have values which lie in the interval \([0,1]\).

These functions actually allow for the zero-deflated Poisson (ZDP) distribution. Here, pstr0 is also permitted to lie in the interval [-1/expm1(lambda), 0]. The resulting probability of a zero count is less than the nominal Poisson value, and the use of pstr0 to stand for the probability of a structural zero loses its meaning. When pstr0 equals -1/expm1(lambda) this corresponds to the positive-Poisson distribution (e.g., see Gaitdpois), also called the zero-truncated Poisson or ZTP.

The zero-modified Poisson (ZMP) is a combination of the ZIP and ZDP and ZTP distributions. The family function

See also

zipoisson, Gaitdpois, dpois, rzinegbin.

Examples

lambda <- 3; pstr0 <- 0.2; x <- (-1):7
(ii <- dzipois(x, lambda, pstr0 = pstr0))
#> [1] 0.00000000 0.23982965 0.11948896 0.17923345 0.17923345 0.13442508 0.08065505
#> [8] 0.04032753 0.01728323
max(abs(cumsum(ii) - pzipois(x, lambda, pstr0 = pstr0)))  # 0?
#> [1] 2.220446e-16
table(rzipois(100, lambda, pstr0 = pstr0))
#> 
#>  0  1  2  3  4  5  6  7  9 10 
#> 29 13 17 15 11  8  3  2  1  1 

table(qzipois(runif(100), lambda, pstr0))
#> 
#>  0  1  2  3  4  5  6  8 
#> 25 11 11 21 19  8  3  2 
round(dzipois(0:10, lambda, pstr0 = pstr0) * 100)  # Similar?
#>  [1] 24 12 18 18 13  8  4  2  1  0  0

if (FALSE)  x <- 0:10
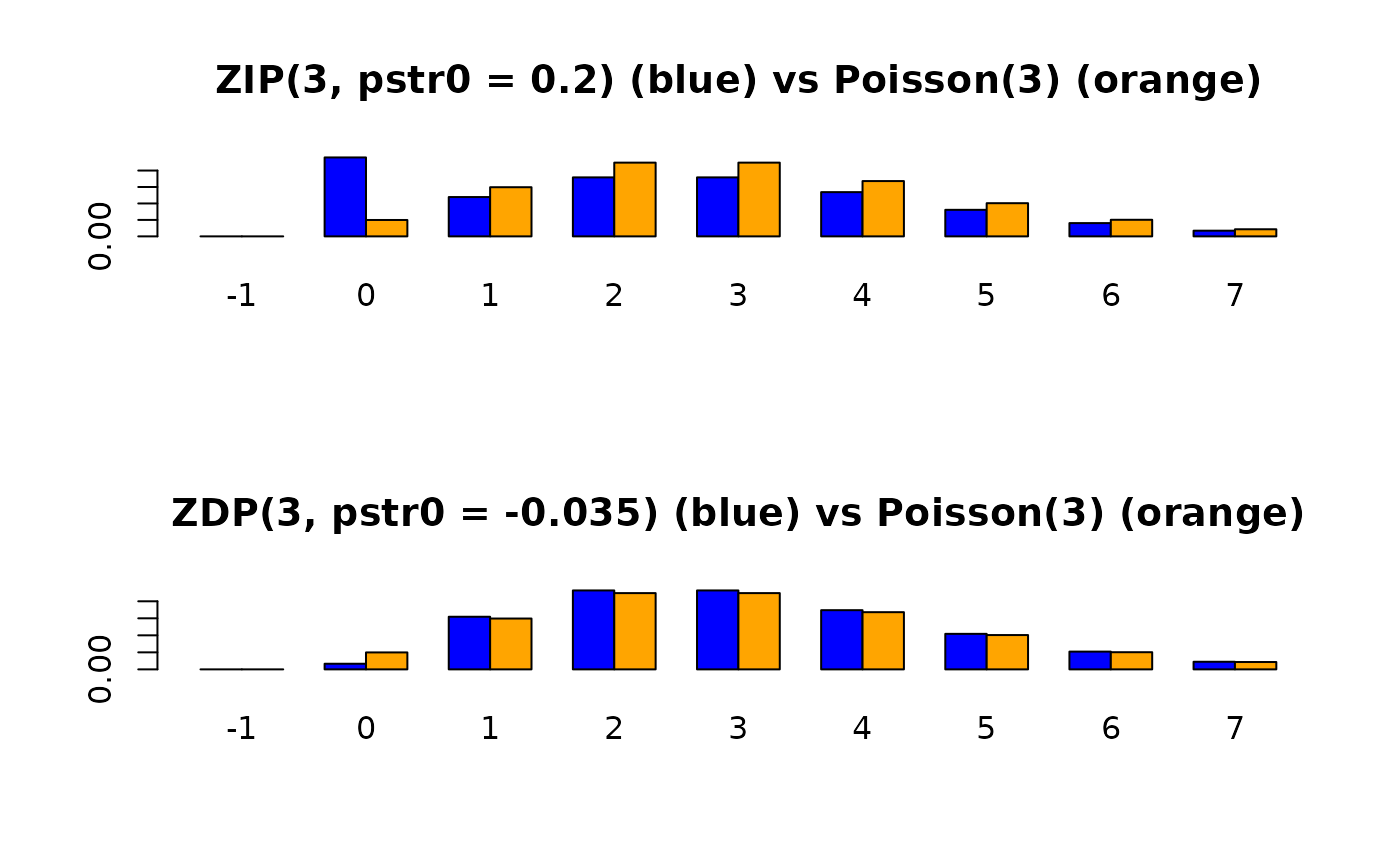
par(mfrow = c(2, 1))  # Zero-inflated Poisson
barplot(rbind(dzipois(x, lambda, pstr0 = pstr0), dpois(x, lambda)),
        beside = TRUE, col = c("blue", "orange"),
        main = paste0("ZIP(", lambda,
                      ", pstr0 = ", pstr0, ") (blue) vs",
                      " Poisson(", lambda, ") (orange)"),
        names.arg = as.character(x))

deflat.limit <- -1 / expm1(lambda)  # Zero-deflated Poisson
newpstr0 <- round(deflat.limit / 1.5, 3)
barplot(rbind(dzipois(x, lambda, pstr0 = newpstr0),
                dpois(x, lambda)),
        beside = TRUE, col = c("blue","orange"),
        main = paste0("ZDP(", lambda, ", pstr0 = ", newpstr0, ")",
                     " (blue) vs Poisson(", lambda, ") (orange)"),
        names.arg = as.character(x))  # \dontrun{}