Print Diagnostic Characteristics of ODE and DAE Solvers

Prints several diagnostics of the simulation to the screen, e.g. number of steps taken, the last step size, ...

# S3 method for class 'deSolve'
diagnostics(obj, Full = FALSE, ...)

Arguments

obj

is the output matrix as produced by one of the integration routines.

Full

when TRUE then all messages will be printed, including the ones that are not relevant for the solver. If FALSE, then only the relevant messages will be printed.

...

optional arguments allowing to extend diagnostics as a generic function.

Value

The integer and real vector with diagnostic values; for function lsodar also the root information.

See tables 2 and 3 in vignette("deSolve") for what these vectors contain.

Note: the number of function evaluations are *without* the extra calls performed to generate the ordinary output variables (if present).

Details

When the integration output is saved as a data.frame, then the required attributes are lost and method diagnostics will not work anymore.

Examples

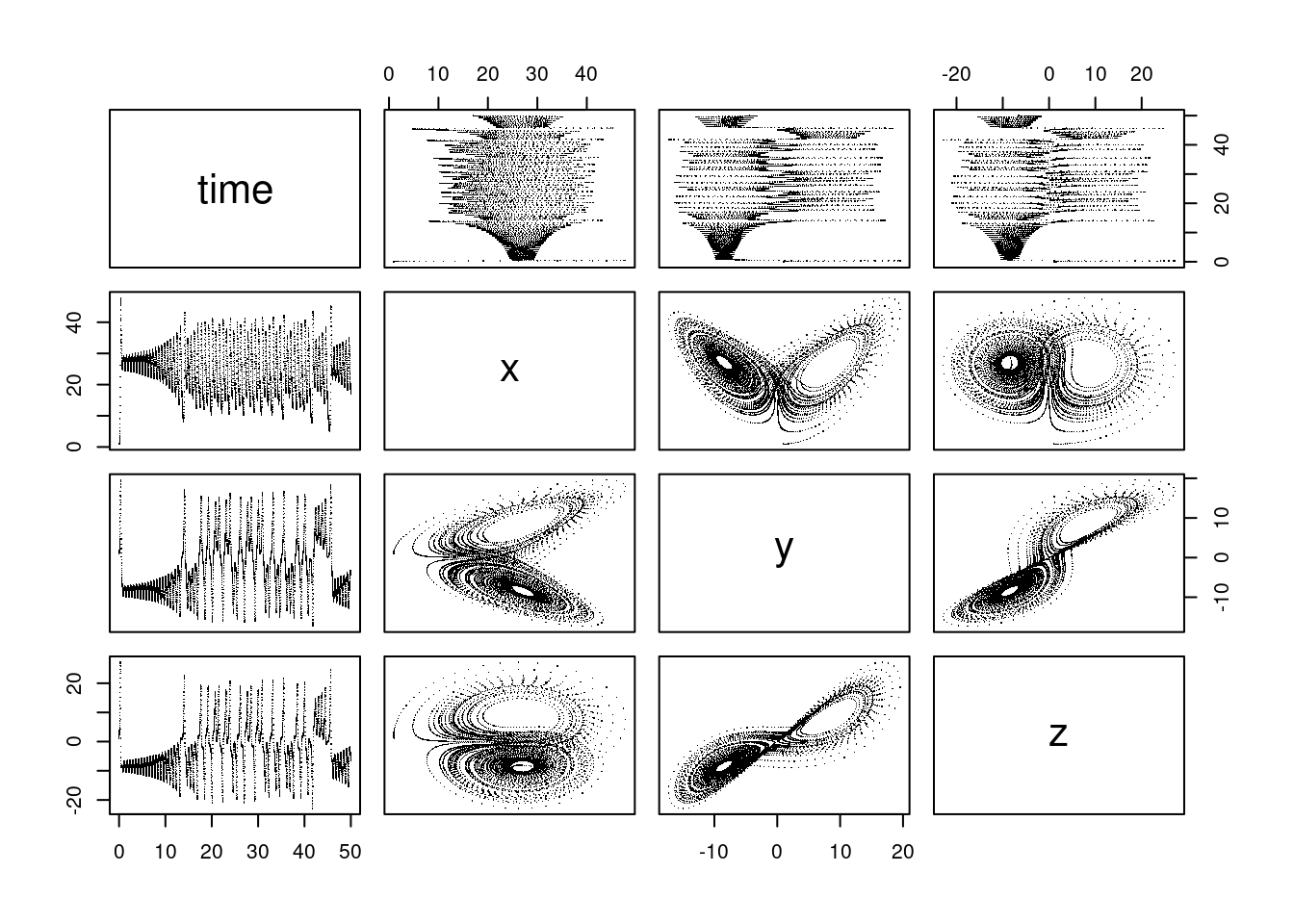
## The famous Lorenz equations: chaos in the earth's atmosphere
## Lorenz 1963. J. Atmos. Sci. 20, 130-141.

chaos <- function(t, state, parameters) {
  with(as.list(c(state)), {

    dx     <- -8/3 * x + y * z
    dy     <- -10 * (y - z)
    dz     <- -x * y + 28 * y - z

    list(c(dx, dy, dz))
  })
}

state <- c(x = 1, y = 1, z = 1)
times <- seq(0, 50, 0.01)
out   <- vode(state, times, chaos, 0)
pairs(out, pch = ".")

diagnostics(out)
#> 
#> --------------------
#> vode return code
#> --------------------
#> 
#>   return code (idid) =  2 
#>   Integration was successful.
#> 
#> --------------------
#> INTEGER values
#> --------------------
#> 
#>   1 The return code : 2 
#>   2 The number of steps taken for the problem so far: 6277 
#>   3 The number of function evaluations for the problem so far: 7205 
#>   4 The number of Jacobian evaluations so far: 108 
#>   5 The method order last used (successfully): 5 
#>   6 The order of the method to be attempted on the next step: 5 
#>   7 If return flag =-4,-5: the largest component in error vector 0 
#>   8 The length of the real work array actually required: 67 
#>   9 The length of the integer work array actually required: 33 
#>  10 The number of matrix LU decompositions so far: 403 
#>  11 The number of nonlinear (Newton) iterations so far: 6878 
#>  
#> --------------------
#> RSTATE values
#> --------------------
#> 
#>   1 The step size in t last used (successfully): 0.01 
#>   2 The step size to be attempted on the next step: 0.01 
#>   3 The current value of the independent variable which the solver has reached: 50.00588 
#>   4 Tolerance scale factor > 1.0 computed when requesting too much accuracy: 0 
#>