Time Lagged Values of State Variables and Derivatives.
timelags.RdFunctions lagvalue and lagderiv provide access to past
(lagged) values of state variables and derivatives.
They are to be used with function dede, to solve delay differential
equations.
lagvalue(t, nr)
lagderiv(t, nr)Arguments
Value
a scalar (or vector) with the lagged value(s).
Details
The lagvalue and lagderiv can only be called during the
integration, the lagged time should not be smaller than the initial
simulation time, nor should it be larger than the current simulation
time.
Cubic Hermite interpolation is used to obtain an accurate interpolant at the requested lagged time.
See also
dede, for how to implement delay differential equations.
Examples
## =============================================================================
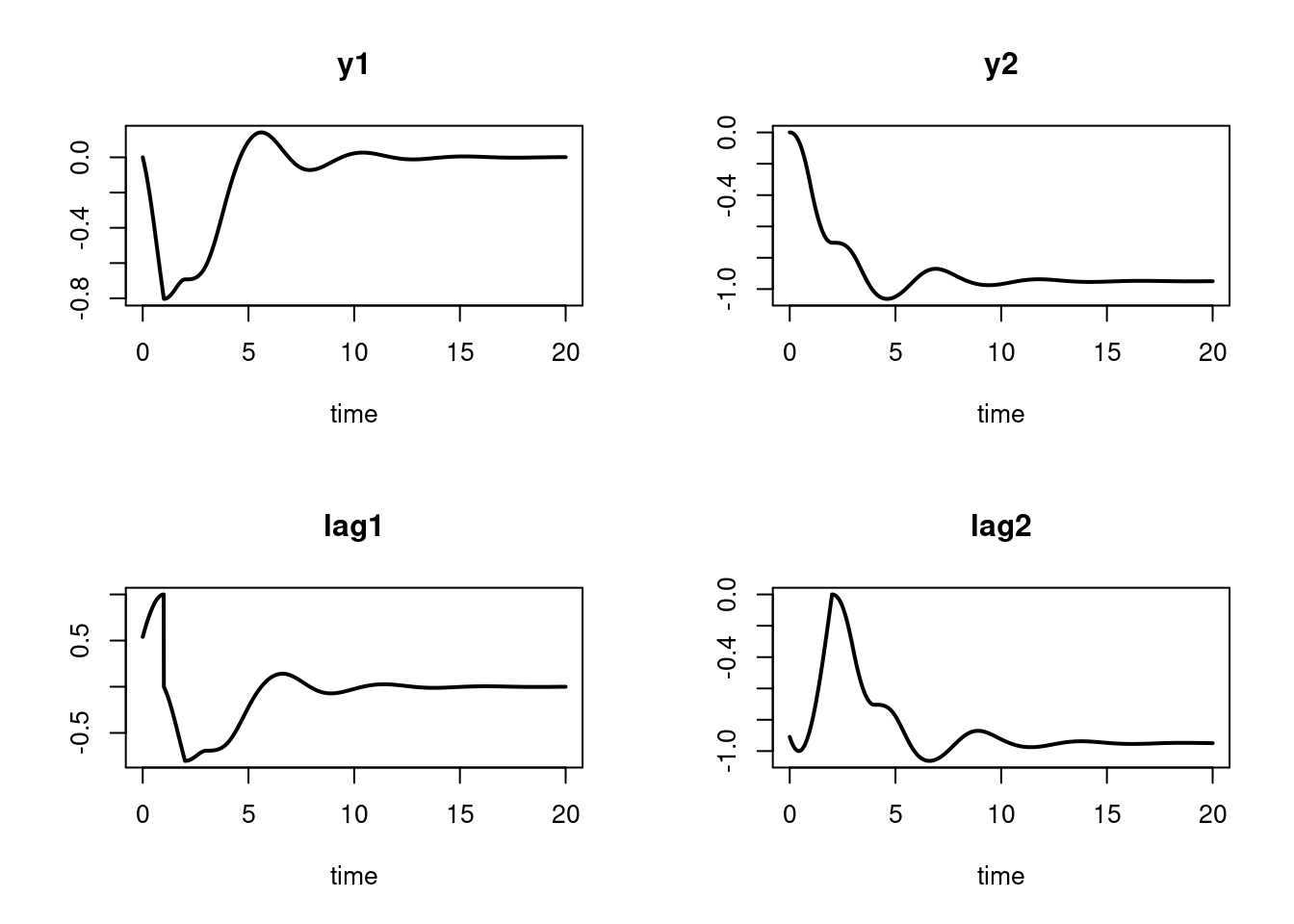
## exercise 6 from Shampine and Thompson, 2000
## solving delay differential equations with dde23
##
## two lag values
## =============================================================================
##-----------------------------
## the derivative function
##-----------------------------
derivs <- function(t, y, parms) {
History <- function(t) c(cos(t), sin(t))
if (t < 1)
lag1 <- History(t - 1)[1]
else
lag1 <- lagvalue(t - 1)[1] # returns a vector; select first element
if (t < 2)
lag2 <- History(t - 2)[2]
else
lag2 <- lagvalue(t - 2,2) # faster than lagvalue(t - 2)[2]
dy1 <- lag1 * lag2
dy2 <- -y[1] * lag2
list(c(dy1, dy2), lag1 = lag1, lag2 = lag2)
}
##-----------------------------
## parameters
##-----------------------------
r <- 3.5; m <- 19
##-----------------------------
## initial values and times
##-----------------------------
yinit <- c(y1 = 0, y2 = 0)
times <- seq(0, 20, by = 0.01)
##-----------------------------
## solve the model
##-----------------------------
yout <- dede(y = yinit, times = times, func = derivs,
parms = NULL, atol = 1e-9)
##-----------------------------
## plot results
##-----------------------------
plot(yout, type = "l", lwd = 2)
 ## =============================================================================
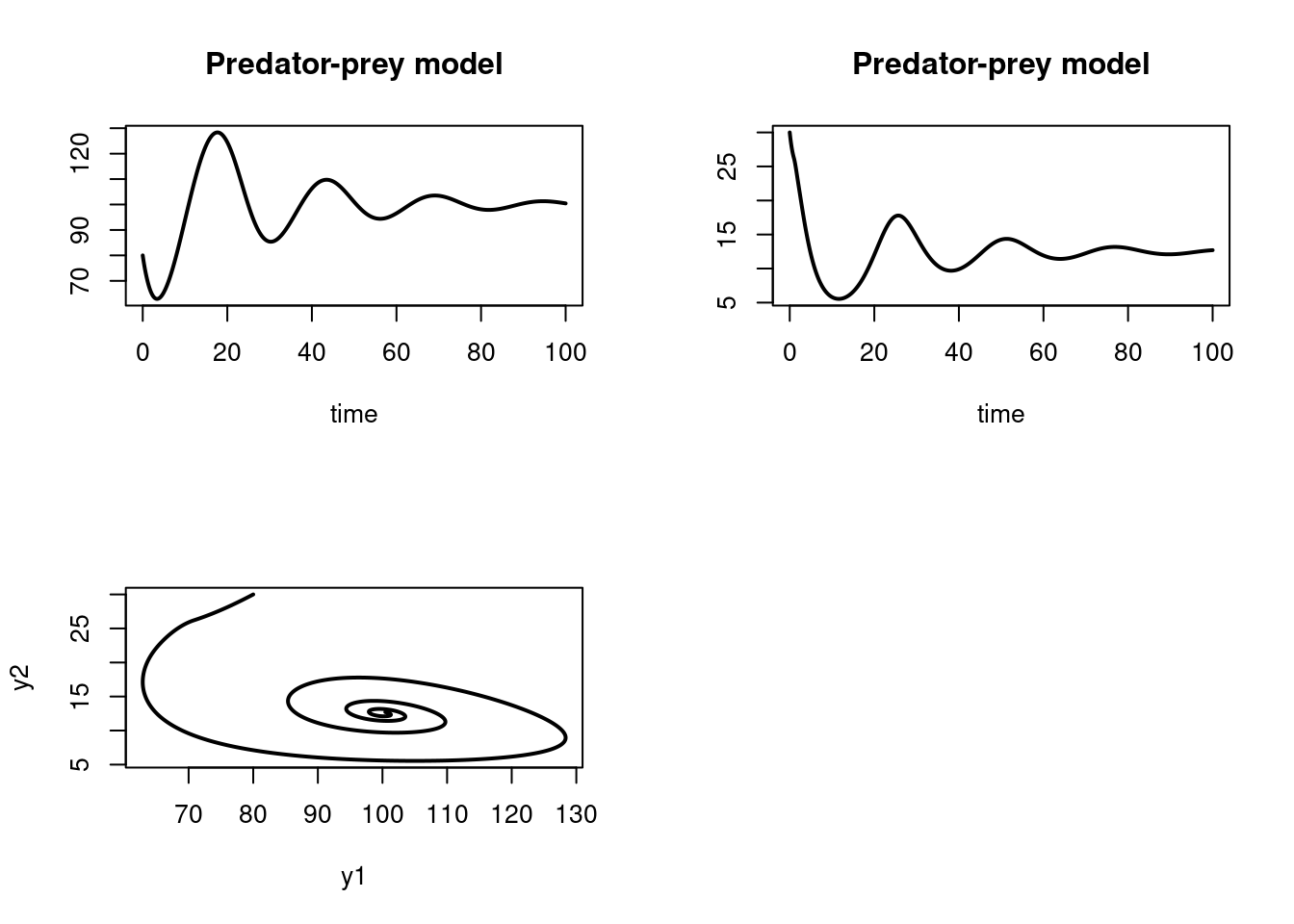
## The predator-prey model with time lags, from Hale
## problem 1 from Shampine and Thompson, 2000
## solving delay differential equations with dde23
##
## a vector with lag valuess
## =============================================================================
##-----------------------------
## the derivative function
##-----------------------------
predprey <- function(t, y, parms) {
tlag <- t - 1
if (tlag < 0)
ylag <- c(80, 30)
else
ylag <- lagvalue(tlag) # returns a vector
dy1 <- a * y[1] * (1 - y[1]/m) + b * y[1] * y[2]
dy2 <- c * y[2] + d * ylag[1] * ylag[2]
list(c(dy1, dy2))
}
##-----------------------------
## parameters
##-----------------------------
a <- 0.25; b <- -0.01; c <- -1 ; d <- 0.01; m <- 200
##-----------------------------
## initial values and times
##-----------------------------
yinit <- c(y1 = 80, y2 = 30)
times <- seq(0, 100, by = 0.01)
#-----------------------------
# solve the model
#-----------------------------
yout <- dede(y = yinit, times = times, func = predprey, parms = NULL)
##-----------------------------
## display, plot results
##-----------------------------
plot(yout, type = "l", lwd = 2, main = "Predator-prey model", mfrow = c(2, 2))
plot(yout[,2], yout[,3], xlab = "y1", ylab = "y2", type = "l", lwd = 2)
diagnostics(yout)
#>
#> --------------------
#> lsoda return code
#> --------------------
#>
#> return code (idid) = 2
#> Integration was successful.
#>
#> --------------------
#> INTEGER values
#> --------------------
#>
#> 1 The return code : 2
#> 2 The number of steps taken for the problem so far: 40133
#> 3 The number of function evaluations for the problem so far: 50033
#> 5 The method order last used (successfully): 3
#> 6 The order of the method to be attempted on the next step: 3
#> 7 If return flag =-4,-5: the largest component in error vector 0
#> 8 The length of the real work array actually required: 52
#> 9 The length of the integer work array actually required: 22
#> 14 The number of Jacobian evaluations and LU decompositions so far: 0
#> 15 The method indicator for the last succesful step,
#> 1=adams (nonstiff), 2= bdf (stiff): 1
#> 16 The current method indicator to be attempted on the next step,
#> 1=adams (nonstiff), 2= bdf (stiff): 1
#>
#> --------------------
#> RSTATE values
#> --------------------
#>
#> 1 The step size in t last used (successfully): 0.0006720412
#> 2 The step size to be attempted on the next step: 0.0006720412
#> 3 The current value of the independent variable which the solver has reached: 100
#> 4 Tolerance scale factor > 1.0 computed when requesting too much accuracy: 0
#> 5 The value of t at the time of the last method switch, if any: 0
#>
## =============================================================================
##
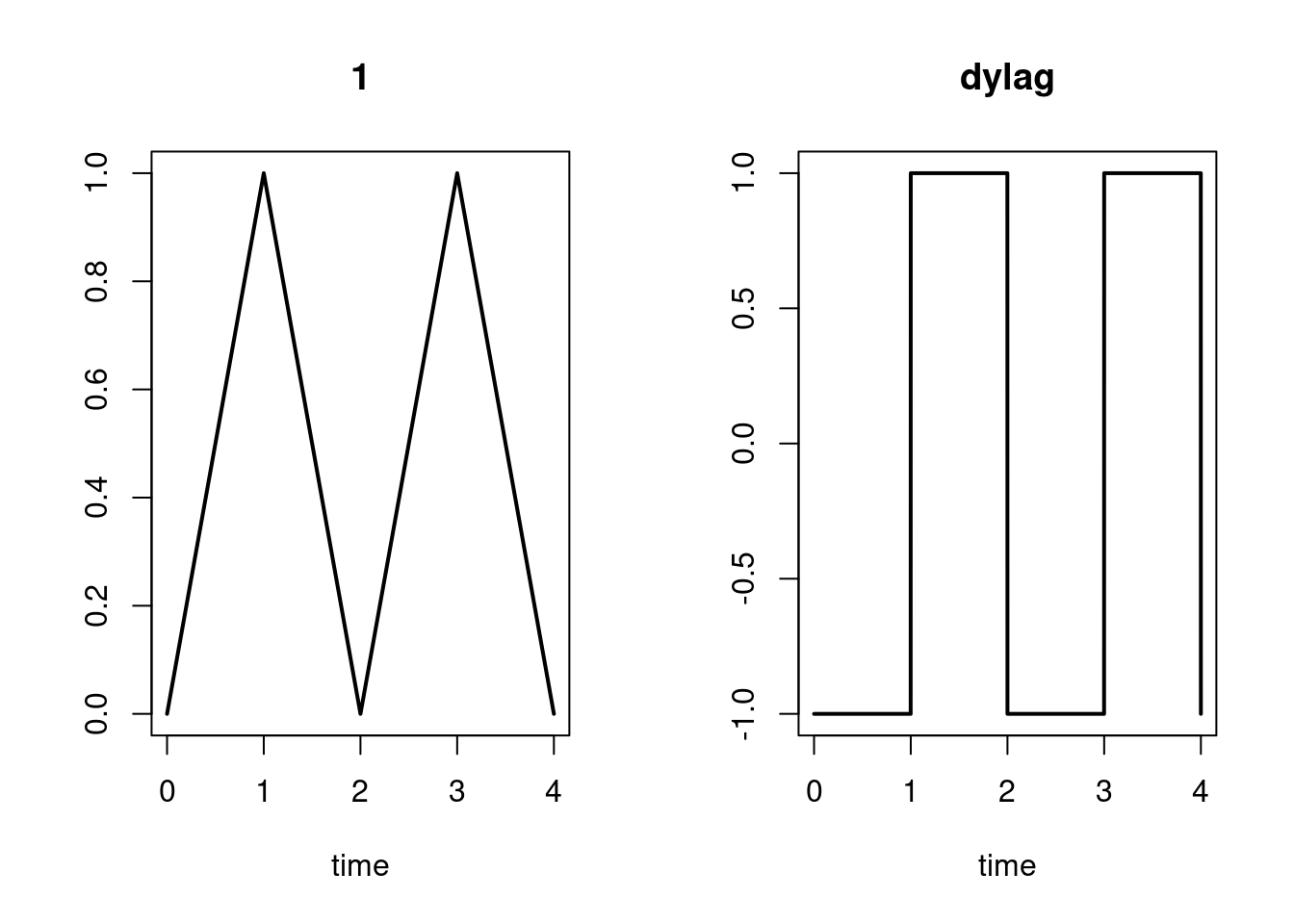
## A neutral delay differential equation (lagged derivative)
## y't = -y'(t-1), y(t) t < 0 = 1/t
##
## =============================================================================
##-----------------------------
## the derivative function
##-----------------------------
derivs <- function(t, y, parms) {
tlag <- t - 1
if (tlag < 0)
dylag <- -1
else
dylag <- lagderiv(tlag)
list(c(dy = -dylag), dylag = dylag)
}
##-----------------------------
## initial values and times
##-----------------------------
yinit <- 0
times <- seq(0, 4, 0.001)
##-----------------------------
## solve the model
##-----------------------------
yout <- dede(y = yinit, times = times, func = derivs, parms = NULL)
##-----------------------------
## display, plot results
##-----------------------------
plot(yout, type = "l", lwd = 2)
## =============================================================================
## The predator-prey model with time lags, from Hale
## problem 1 from Shampine and Thompson, 2000
## solving delay differential equations with dde23
##
## a vector with lag valuess
## =============================================================================
##-----------------------------
## the derivative function
##-----------------------------
predprey <- function(t, y, parms) {
tlag <- t - 1
if (tlag < 0)
ylag <- c(80, 30)
else
ylag <- lagvalue(tlag) # returns a vector
dy1 <- a * y[1] * (1 - y[1]/m) + b * y[1] * y[2]
dy2 <- c * y[2] + d * ylag[1] * ylag[2]
list(c(dy1, dy2))
}
##-----------------------------
## parameters
##-----------------------------
a <- 0.25; b <- -0.01; c <- -1 ; d <- 0.01; m <- 200
##-----------------------------
## initial values and times
##-----------------------------
yinit <- c(y1 = 80, y2 = 30)
times <- seq(0, 100, by = 0.01)
#-----------------------------
# solve the model
#-----------------------------
yout <- dede(y = yinit, times = times, func = predprey, parms = NULL)
##-----------------------------
## display, plot results
##-----------------------------
plot(yout, type = "l", lwd = 2, main = "Predator-prey model", mfrow = c(2, 2))
plot(yout[,2], yout[,3], xlab = "y1", ylab = "y2", type = "l", lwd = 2)
diagnostics(yout)
#>
#> --------------------
#> lsoda return code
#> --------------------
#>
#> return code (idid) = 2
#> Integration was successful.
#>
#> --------------------
#> INTEGER values
#> --------------------
#>
#> 1 The return code : 2
#> 2 The number of steps taken for the problem so far: 40133
#> 3 The number of function evaluations for the problem so far: 50033
#> 5 The method order last used (successfully): 3
#> 6 The order of the method to be attempted on the next step: 3
#> 7 If return flag =-4,-5: the largest component in error vector 0
#> 8 The length of the real work array actually required: 52
#> 9 The length of the integer work array actually required: 22
#> 14 The number of Jacobian evaluations and LU decompositions so far: 0
#> 15 The method indicator for the last succesful step,
#> 1=adams (nonstiff), 2= bdf (stiff): 1
#> 16 The current method indicator to be attempted on the next step,
#> 1=adams (nonstiff), 2= bdf (stiff): 1
#>
#> --------------------
#> RSTATE values
#> --------------------
#>
#> 1 The step size in t last used (successfully): 0.0006720412
#> 2 The step size to be attempted on the next step: 0.0006720412
#> 3 The current value of the independent variable which the solver has reached: 100
#> 4 Tolerance scale factor > 1.0 computed when requesting too much accuracy: 0
#> 5 The value of t at the time of the last method switch, if any: 0
#>
## =============================================================================
##
## A neutral delay differential equation (lagged derivative)
## y't = -y'(t-1), y(t) t < 0 = 1/t
##
## =============================================================================
##-----------------------------
## the derivative function
##-----------------------------
derivs <- function(t, y, parms) {
tlag <- t - 1
if (tlag < 0)
dylag <- -1
else
dylag <- lagderiv(tlag)
list(c(dy = -dylag), dylag = dylag)
}
##-----------------------------
## initial values and times
##-----------------------------
yinit <- 0
times <- seq(0, 4, 0.001)
##-----------------------------
## solve the model
##-----------------------------
yout <- dede(y = yinit, times = times, func = derivs, parms = NULL)
##-----------------------------
## display, plot results
##-----------------------------
plot(yout, type = "l", lwd = 2)