Unbounded density estimator

Unbounded density estimator using stats::density().

Supports automatic partial function application with waived arguments.

density_unbounded(
  x,
  weights = NULL,
  n = 501,
  bandwidth = "dpi",
  adjust = 1,
  kernel = "gaussian",
  trim = TRUE,
  adapt = 1,
  na.rm = FALSE,
  ...,
  range_only = FALSE
)

Arguments

x

<numeric> Sample to compute a density estimate for.

weights

<numeric | NULL> Optional weights to apply to x.

n

<scalar numeric> The number of grid points to evaluate the density estimator at.

bandwidth

<scalar numeric | function | string> Bandwidth of the density estimator. One of:

a numeric: the bandwidth, as the standard deviation of the kernel
a function: a function taking x (the sample) and returning the bandwidth
a string: the suffix of the name of a function starting with "bandwidth_" that will be used to determine the bandwidth. See bandwidth for a list.

adjust

<scalar numeric> Value to multiply the bandwidth of the density estimator by. Default 1.

kernel

<string> The smoothing kernel to be used. This must partially match one of "gaussian", "rectangular", "triangular", "epanechnikov", "biweight", "cosine", or "optcosine". See stats::density().

trim

<scalar logical> Should the density estimate be trimmed to the range of the data? Default TRUE.

adapt

<positive integer> (very experimental) The name and interpretation of this argument are subject to change without notice. If adapt > 1, uses an adaptive approach to calculate the density. First, uses the adaptive bandwidth algorithm of Abramson (1982) to determine local (pointwise) bandwidths, then groups these bandwidths into adapt groups, then calculates and sums the densities from each group. You can set this to a very large number (e.g. Inf) for a fully adaptive approach, but this will be very slow; typically something around 100 yields nearly identical results.

na.rm

<scalar logical> Should missing (NA) values in x be removed?

...

Additional arguments (ignored).

range_only

<scalar logical> If TRUE, the range of the output of this density estimator is computed and is returned in the $x element of the result, and c(NA, NA) is returned in $y. This gives a faster way to determine the range of the output than density_XXX(n = 2).

Value

An object of class "density", mimicking the output format of stats::density(), with the following components:

x: The grid of points at which the density was estimated.
y: The estimated density values.
bw: The bandwidth.
n: The sample size of the x input argument.
call: The call used to produce the result, as a quoted expression.
data.name: The deparsed name of the x input argument.
has.na: Always FALSE (for compatibility).
cdf: Values of the (possibly weighted) empirical cumulative distribution function at x. See weighted_ecdf().

This allows existing methods for density objects, like print() and plot(), to work if desired. This output format (and in particular, the x and y components) is also the format expected by the density argument of the stat_slabinterval() and the smooth_ family of functions.

Examples

library(distributional)
library(dplyr)
library(ggplot2)

# For compatibility with existing code, the return type of density_unbounded()
# is the same as stats::density(), ...
set.seed(123)
x = rbeta(5000, 1, 3)
d = density_unbounded(x)
d
#> 
#> Call:
#> 	density_unbounded(x = x)
#> 
#> Data: x (5000 obs.);	Bandwidth 'bw' = 0.01647
#> 
#>        x                   y          
#>  Min.   :0.0000338   Min.   :0.01634  
#>  1st Qu.:0.2368066   1st Qu.:0.26382  
#>  Median :0.4735795   Median :0.91021  
#>  Mean   :0.4735795   Mean   :1.03440  
#>  3rd Qu.:0.7103524   3rd Qu.:1.64200  
#>  Max.   :0.9471253   Max.   :2.77205  

# ... thus, while designed for use with the `density` argument of
# stat_slabinterval(), output from density_unbounded() can also be used with
# base::plot():
plot(d)


# here we'll use the same data as above, but pick either density_bounded()
# or density_unbounded() (which is equivalent to stats::density()). Notice
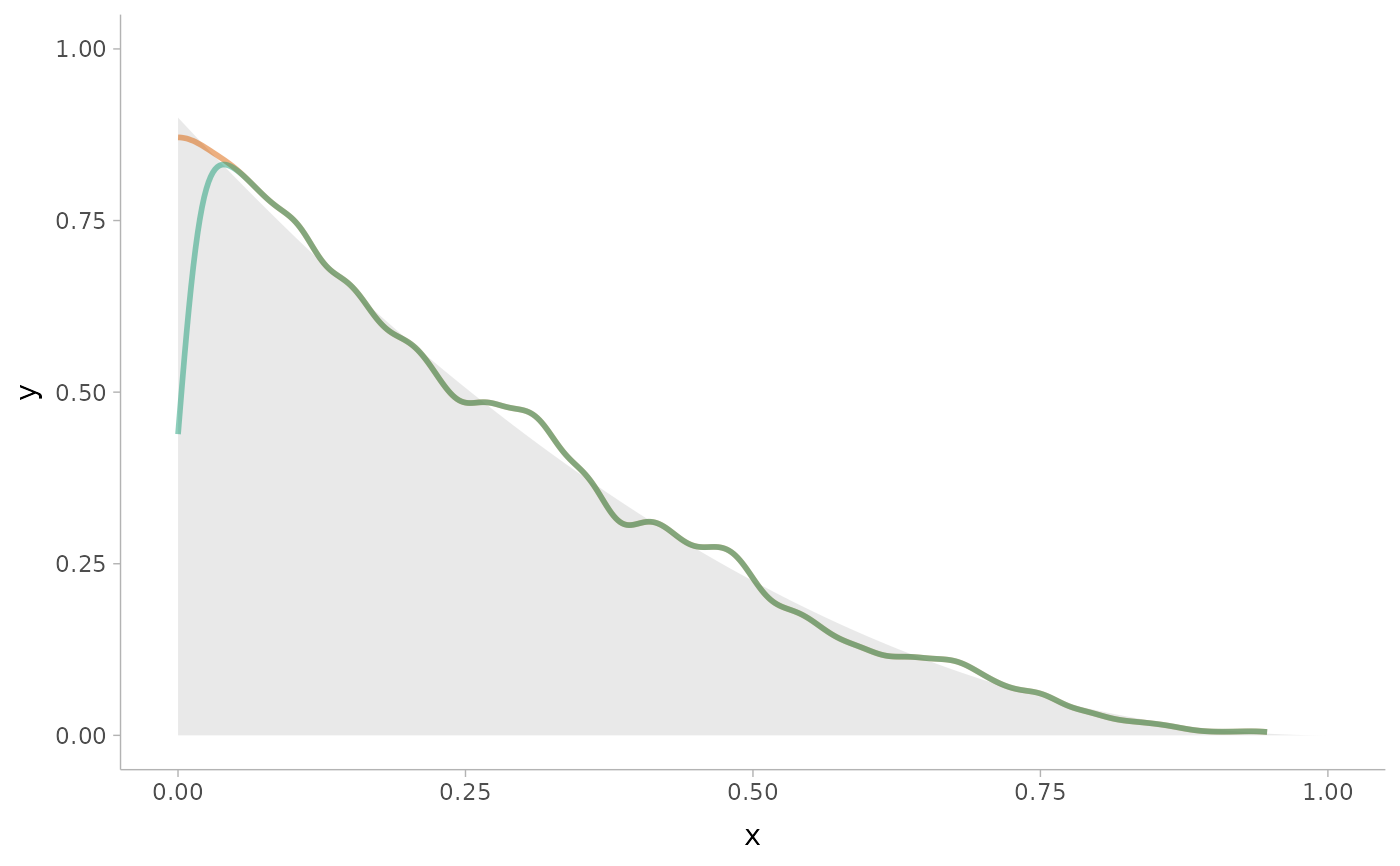
# how the bounded density (green) is biased near the boundary of the support,
# while the unbounded density is not.
data.frame(x) %>%
  ggplot() +
  stat_slab(
    aes(xdist = dist), data = data.frame(dist = dist_beta(1, 3)),
    alpha = 0.25
  ) +
  stat_slab(aes(x), density = "bounded", fill = NA, color = "#d95f02", alpha = 0.5) +
  stat_slab(aes(x), density = "unbounded", fill = NA, color = "#1b9e77", alpha = 0.5) +
  scale_thickness_shared() +
  theme_ggdist()

Arguments

Value

See also

Examples