Class "kqr"
kqr-class.RdThe Kernel Quantile Regression object class
Objects from the Class
Objects can be created by calls of the form new("kqr", ...).
or by calling the kqr function
Slots
kernelf:Object of class
"kfunction"contains the kernel function usedkpar:Object of class
"list"contains the kernel parameter usedcoef:Object of class
"ANY"containing the model parametersparam:Object of class
"list"contains the cost parameter C and tau parameter usedkcall:Object of class
"list"contains the used function callterms:Object of class
"ANY"contains the terms representation of the symbolic model used (when using a formula)xmatrix:Object of class
"input"containing the data matrix usedymatrix:Object of class
"output"containing the response matrixfitted:Object of class
"output"containing the fitted valuesalpha:Object of class
"listI"containing the computes alpha valuesb:Object of class
"numeric"containing the offset of the model.scalingObject of class
"ANY"containing the scaling coefficients of the data (when casescaled = TRUEis used).error:Object of class
"numeric"containing the training errorcross:Object of class
"numeric"containing the cross validation errorn.action:Object of class
"ANY"containing the action performed in NAnclass:Inherited from class
vm, not used in kqrlev:Inherited from class
vm, not used in kqrtype:Inherited from class
vm, not used in kqr
Methods
- coef
signature(object = "kqr"): returns the coefficients (alpha) of the model- alpha
signature(object = "kqr"): returns the alpha vector (identical tocoef)- b
signature(object = "kqr"): returns the offset beta of the model.- cross
signature(object = "kqr"): returns the cross validation error- error
signature(object = "kqr"): returns the training error- fitted
signature(object = "vm"): returns the fitted values- kcall
signature(object = "kqr"): returns the call performed- kernelf
signature(object = "kqr"): returns the kernel function used- kpar
signature(object = "kqr"): returns the kernel parameter used- param
signature(object = "kqr"): returns the cost regularization parameter C and tau used- xmatrix
signature(object = "kqr"): returns the data matrix used- ymatrix
signature(object = "kqr"): returns the response matrix used- scaling
signature(object = "kqr"): returns the scaling coefficients of the data (whenscaled = TRUEis used)
See also
Examples
# create data
x <- sort(runif(300))
y <- sin(pi*x) + rnorm(300,0,sd=exp(sin(2*pi*x)))
# first calculate the median
qrm <- kqr(x, y, tau = 0.5, C=0.15)
#> Using automatic sigma estimation (sigest) for RBF or laplace kernel
# predict and plot
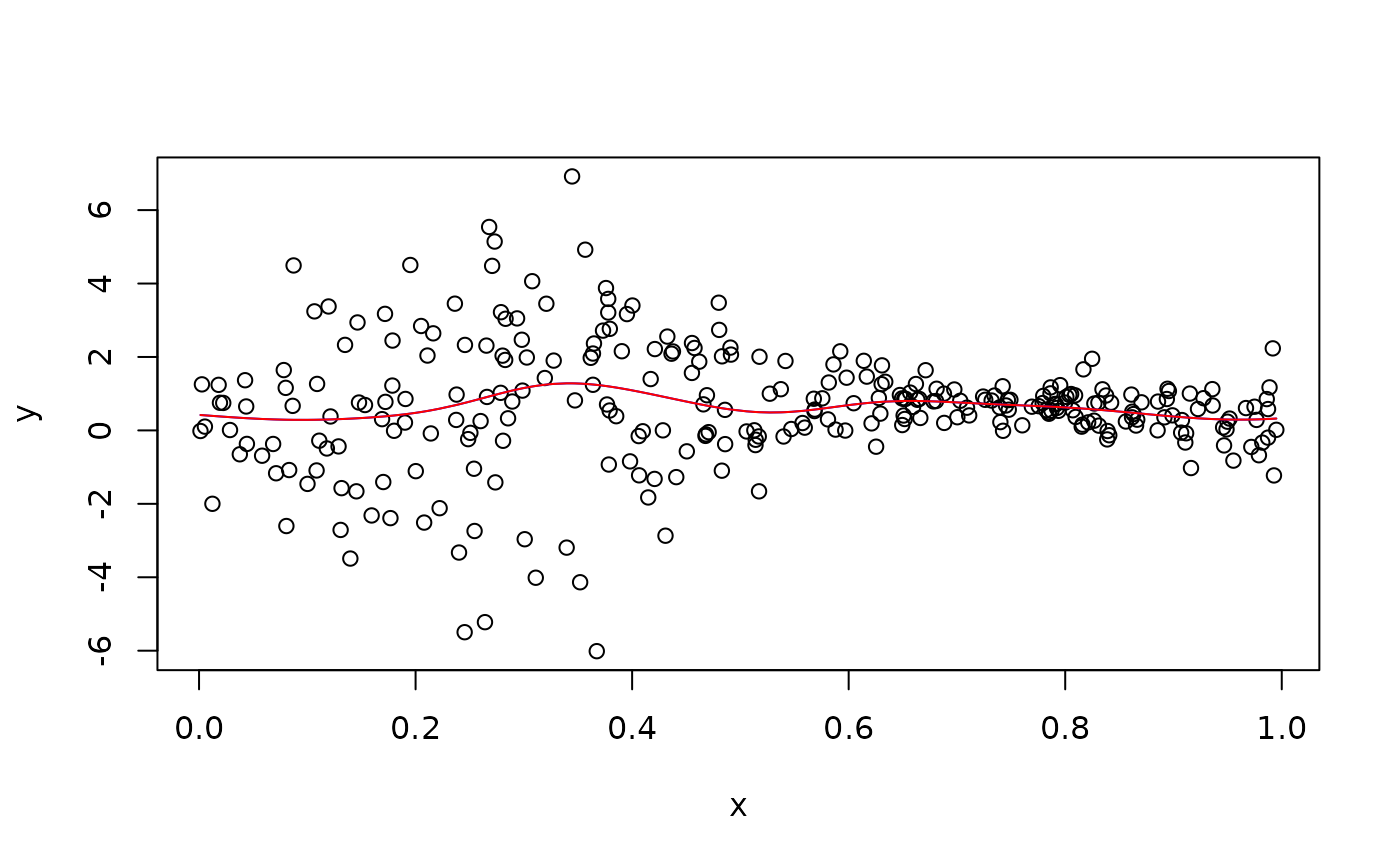
plot(x, y)
ytest <- predict(qrm, x)
lines(x, ytest, col="blue")
# calculate 0.9 quantile
qrm <- kqr(x, y, tau = 0.9, kernel = "rbfdot",
kpar = list(sigma = 10), C = 0.15)
#> Error in solve.default(AP, c(c.x, c.y)): system is computationally singular: reciprocal condition number = 3.47396e-19
ytest <- predict(qrm, x)
lines(x, ytest, col="red")
# print model coefficients and other information
coef(qrm)
#> [1] -0.074597241 0.074786378 -0.074450467 -0.074920888 0.074794247
#> [6] 0.074531278 0.074532596 -0.074527944 -0.074823458 0.074839260
#> [11] 0.074440982 -0.074746198 -0.074825918 -0.074738608 -0.074880462
#> [16] 0.074879722 0.074801642 -0.074934933 -0.074873671 0.074488761
#> [21] 0.074955762 -0.074895286 0.074931737 -0.074871646 0.074833855
#> [26] -0.074697413 -0.074769209 0.074936514 0.072598029 -0.074751350
#> [31] -0.074933641 -0.074897828 0.074905366 -0.074951929 -0.074906614
#> [36] 0.074921376 0.074556592 0.074477073 -0.074923384 -0.071875869
#> [41] -0.074891649 0.074931525 0.074558978 -0.074927499 0.074792257
#> [46] 0.074911574 -0.074574542 -0.074209158 0.074602831 0.074954953
#> [51] -0.074882763 0.074919197 -0.074935927 0.074888103 -0.074696805
#> [56] 0.074912065 -0.074926897 0.074927610 -0.074576197 0.074403247
#> [61] -0.074954596 -0.074973272 0.074885373 -0.074837125 -0.074797095
#> [66] -0.074891813 -0.074942676 -0.074684610 -0.074975068 0.074862605
#> [71] 0.021113865 0.074959141 0.074945281 0.074955421 -0.074917794
#> [76] 0.058921616 0.074917586 0.074825339 -0.074892819 0.074797895
#> [81] 0.074900235 -0.074771870 -0.074425703 0.074897988 0.074852985
#> [86] -0.069994433 -0.074956653 0.074757889 0.074933961 -0.074968726
#> [91] 0.074109730 0.074913973 0.074673467 -0.074959699 0.074968980
#> [96] -0.074668019 -0.074971092 0.074945055 0.074707047 -0.017297631
#> [101] 0.074754363 0.074818309 -0.074977791 0.074866802 0.074928513
#> [106] -0.074674882 0.074919873 0.074904938 -0.074917283 -0.074752909
#> [111] 0.074870558 -0.074801576 0.074791566 0.074891779 -0.074920027
#> [116] 0.074904062 -0.074886593 -0.074926979 -0.074867161 -0.074937538
#> [121] 0.074475114 -0.074921879 0.074844718 -0.074831454 -0.074946474
#> [126] 0.074894852 0.074858979 0.074866888 -0.074920748 -0.074883152
#> [131] 0.074759446 0.074885805 0.074880307 0.074850013 0.065396610
#> [136] -0.074795183 -0.074776280 0.074417482 -0.074748207 0.074931861
#> [141] 0.074928219 -0.074870748 0.074896895 -0.067731701 -0.074809997
#> [146] 0.074903779 0.074894673 -0.074626828 -0.074585580 -0.074788002
#> [151] -0.074746362 -0.074703896 -0.074909190 0.074898663 0.074705167
#> [156] 0.074725978 -0.074703173 0.074890003 -0.074561546 -0.074372087
#> [161] -0.074562103 0.074531272 -0.068061571 0.011249809 0.074464954
#> [166] -0.074388962 0.074741089 0.074857455 -0.074696832 0.074886166
#> [171] -0.074726241 0.074763686 -0.074889454 0.074850995 0.074727396
#> [176] -0.074701512 -0.074872492 0.072247406 -0.074652628 0.074487720
#> [181] 0.074794077 0.074604533 0.073411285 0.061072815 -0.074761475
#> [186] -0.074674361 -0.041082557 -0.074715970 -0.016960863 0.073754373
#> [191] -0.074091911 0.074549555 0.003732177 0.059759231 -0.074651468
#> [196] 0.074781277 -0.066224024 -0.050775949 0.074414569 0.074129539
#> [201] -0.074721089 0.074463944 -0.074665103 0.059905873 -0.073669847
#> [206] -0.074625583 0.073771468 0.072581512 0.072370417 0.074093691
#> [211] -0.073071391 -0.074663950 0.074602628 -0.074759281 -0.070267306
#> [216] 0.073248232 -0.073714872 0.073415200 -0.074671969 -0.068709382
#> [221] -0.052985243 0.073421229 0.074389861 -0.072943759 -0.073707535
#> [226] -0.074078639 0.074540292 0.074662010 -0.073302472 0.072870199
#> [231] 0.072232214 -0.069347429 -0.072927593 0.074705299 0.073741283
#> [236] 0.074435180 0.074524900 0.074560080 -0.071759873 0.074527881
#> [241] -0.074275643 -0.074614283 -0.074576007 0.074842105 -0.074498779
#> [246] 0.074877737 -0.074410086 0.073828436 0.074065741 -0.074563672
#> [251] 0.074689089 0.074606261 -0.074767708 -0.074658556 -0.074718398
#> [256] 0.074232854 -0.074278742 0.074659403 -0.073524140 0.068810283
#> [261] -0.068853253 -0.074499088 -0.073975952 0.074463009 -0.074559795
#> [266] 0.074561956 -0.068677185 0.074627893 0.074759285 0.074736851
#> [271] 0.070446407 -0.074577304 -0.072219647 -0.074729916 -0.074582652
#> [276] 0.074722570 -0.074872569 0.074299229 0.074674972 0.074785812
#> [281] 0.074550221 -0.074161335 -0.074735139 -0.074342772 -0.070998124
#> [286] 0.070050397 -0.074840015 0.074482275 -0.074748243 0.074536078
#> [291] -0.050221287 -0.074813896 -0.074703254 0.074668867 0.074396790
#> [296] -0.074633336 0.074801729 0.074905829 -0.074881626 -0.074421135
b(qrm)
#> [1] 0.01625149
error(qrm)
#> [1] 0.3251391 0.4900000
kernelf(qrm)
#> new("rbfkernel", .Data = function (x, y = NULL)
#> {
#> if (!is(x, "vector"))
#> stop("x must be a vector")
#> if (!is(y, "vector") && !is.null(y))
#> stop("y must a vector")
#> if (is(x, "vector") && is.null(y)) {
#> return(1)
#> }
#> if (is(x, "vector") && is(y, "vector")) {
#> if (!length(x) == length(y))
#> stop("number of dimension must be the same on both data points")
#> return(exp(sigma * (2 * crossprod(x, y) - crossprod(x) -
#> crossprod(y))))
#> }
#> }, kpar = list(sigma = 8.47323510976951))
#> <bytecode: 0x564204d155f8>
#> <environment: 0x56420642f240>
#> attr(,"kpar")
#> attr(,"kpar")$sigma
#> [1] 8.473235
#>
#> attr(,"class")
#> [1] "rbfkernel"
#> attr(,"class")attr(,"package")
#> [1] "kernlab"