twCoefLogitnormE

Estimating coefficients of logitnormal distribution from expected value, i.e. mean, and upper quantile.

twCoefLogitnormE(mean, quant, perc = c(0.975), 
    method = "BFGS", theta0 = c(mu = 0, sigma = 1), 
    returnDetails = FALSE, ...)

Arguments

mean

the expected value of the density function

quant

the quantile values

perc

the probabilities for which the quantiles were specified

method

method of optimization (see optim)

theta0

starting parameters

returnDetails

if TRUE, the full output of optim is returned with attribute resOptim

...

further arguments to optim

Value

named numeric matrix with estimated parameters of the logitnormal distribution. colnames: c("mu","sigma")

Author

Thomas Wutzler

See also

logitnorm

Examples

# estimate the parameters
(thetaE <- twCoefLogitnormE(0.7,0.9))
#>             mu     sigma
#> [1,] 0.9253262 0.6489384

x <- seq(0,1,length.out = 41)[-c(1,41)]  # plotting grid
px <- plogitnorm(x,mu = thetaE[1],sigma = thetaE[2])  #percentiles function
plot(px~x); abline(v = c(0.7,0.9),col = "gray"); abline(h = c(0.5,0.975),col = "gray")

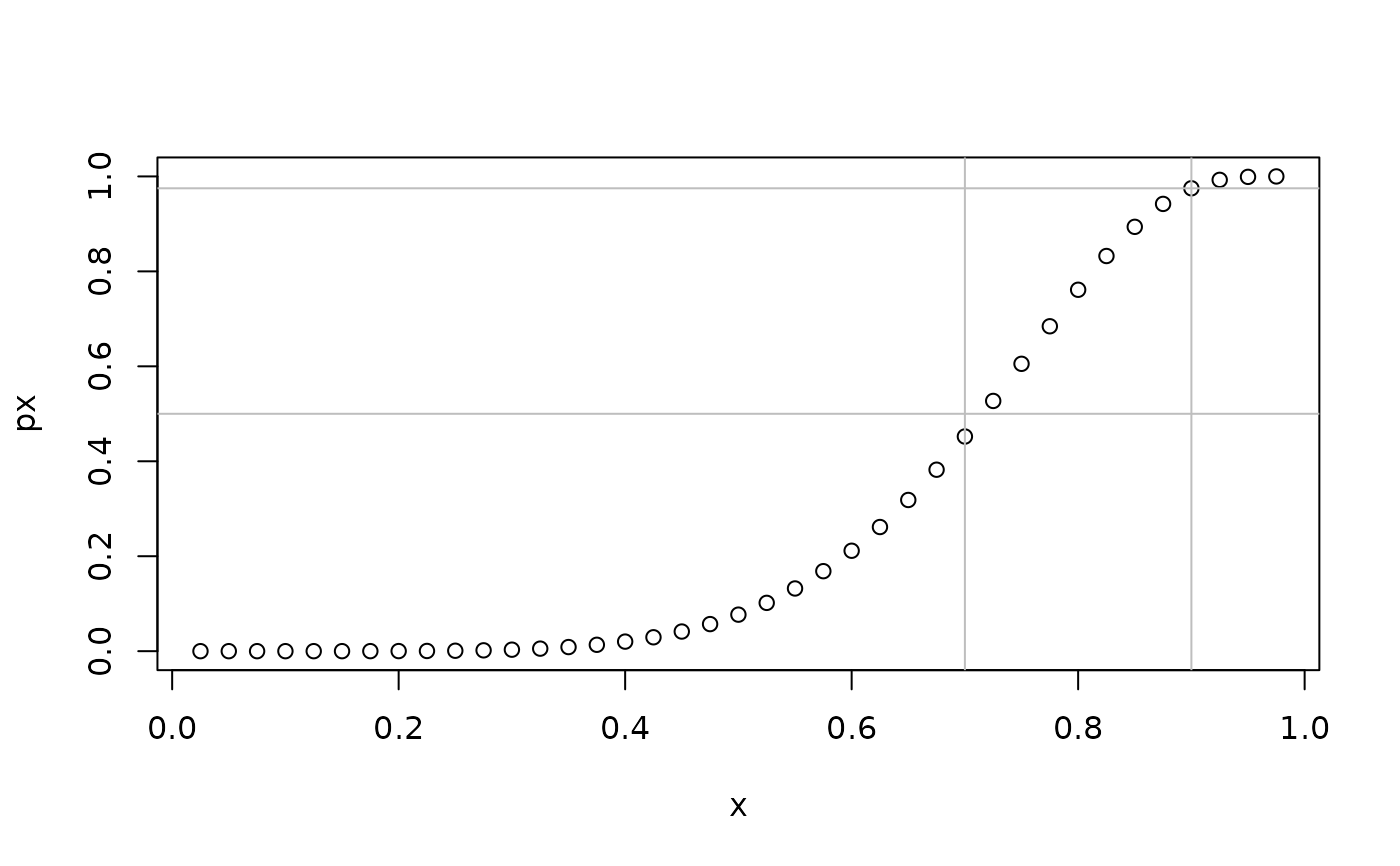dx <- dlogitnorm(x,mu = thetaE[1],sigma = thetaE[2])  #density function
plot(dx~x); abline(v = c(0.7,0.9),col = "gray")


z <- rlogitnorm(1e5, mu = thetaE[1],sigma = thetaE[2])
mean(z)  # about 0.7
#> [1] 0.699682

# vectorized
(theta <- twCoefLogitnormE(mean = seq(0.4,0.8,by = 0.1),quant = 0.9))
#>                 mu     sigma
#> [1,] -5.553675e-01 1.4044088
#> [2,]  1.774359e-07 1.1210528
#> [3,]  4.727770e-01 0.8798354
#> [4,]  9.253262e-01 0.6489384
#> [5,]  1.431068e+00 0.3909022