Generate Tweedie random deviates

Generates Tweedie random deviates, for powers between 1 and 2.

rTweedie(mu,p=1.5,phi=1)

Arguments

mu

vector of expected values for the deviates to be generated. One deviate generated for each element of mu.

p

the variance of a deviate is proportional to its mean, mu to the power p. p must be between 1 and 2. 1 is Poisson like (exactly Poisson if phi=1), 2 is gamma.

phi

The scale parameter. Variance of the deviates is given by is phi*mu^p.

Value

A vector of random deviates from a Tweedie distribution, expected value vector mu, variance vector phi*mu^p.

Details

A Tweedie random variable with 1<p<2 is a sum of N gamma random variables where N has a Poisson distribution, with mean mu^(2-p)/((2-p)*phi). The Gamma random variables that are summed have shape parameter (2-p)/(p-1) and scale parameter phi*(p-1)*mu^(p-1) (note that this scale parameter is different from the scale parameter for a GLM with Gamma errors).

This is a restricted, but faster, version of rtweedie from the tweedie package.

Author

Simon N. Wood simon.wood@r-project.org

References

Peter K Dunn (2009). tweedie: Tweedie exponential family models. R package version 2.0.2. https://cran.r-project.org/package=tweedie

See also

ldTweedie, Tweedie

Examples

 library(mgcv)
 f2 <- function(x) 0.2 * x^11 * (10 * (1 - x))^6 + 10 *
            (10 * x)^3 * (1 - x)^10
 n <- 300
 x <- runif(n)
 mu <- exp(f2(x)/3+.1);x <- x*10 - 4
 y <- rTweedie(mu,p=1.5,phi=1.3)
 b <- gam(y~s(x,k=20),family=Tweedie(p=1.5))
 b
#> 
#> Family: Tweedie(1.5) 
#> Link function: log 
#> 
#> Formula:
#> y ~ s(x, k = 20)
#> 
#> Estimated degrees of freedom:
#> 9.06  total = 10.06 
#> 
#> GCV score: 1.638633     
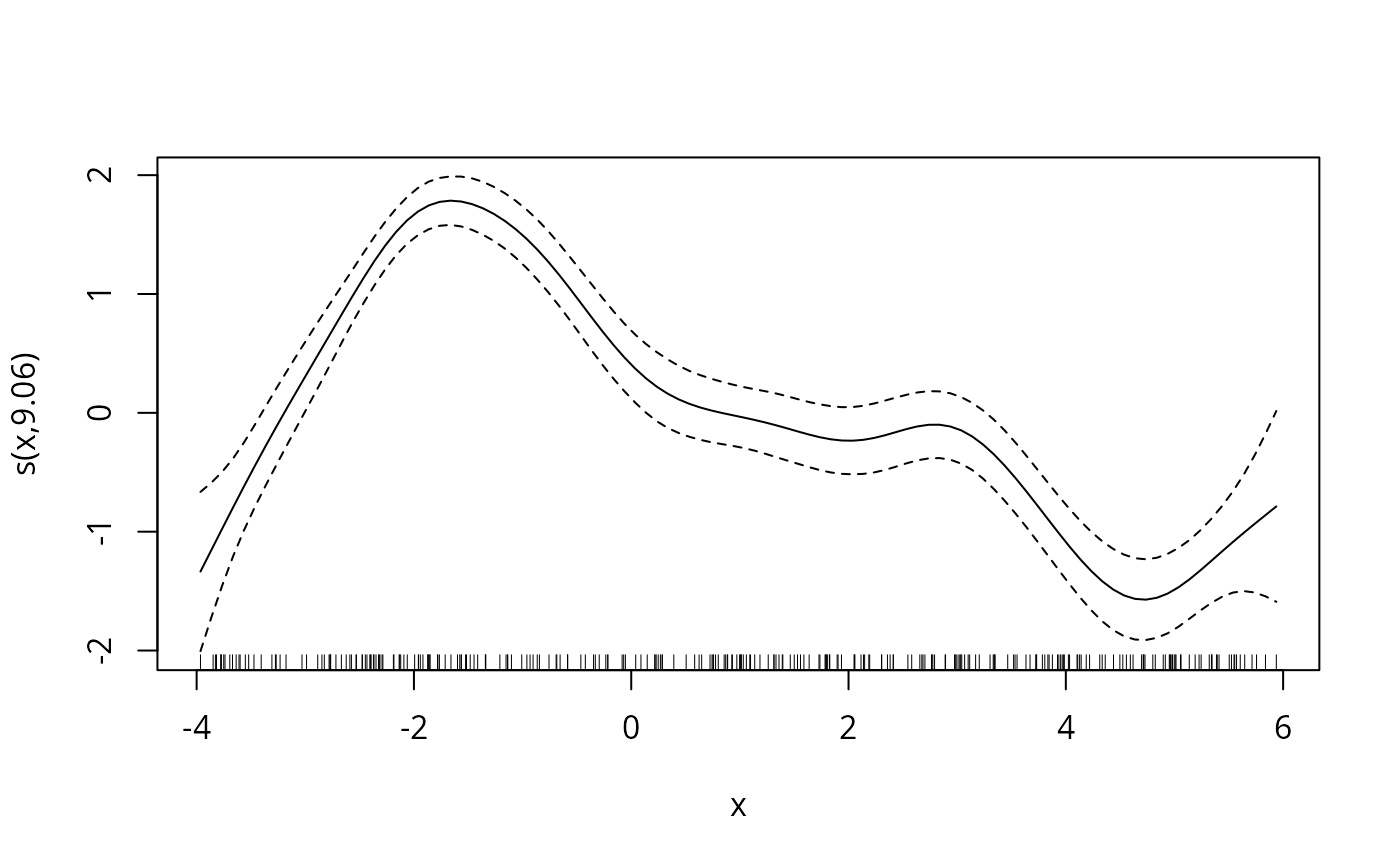
 plot(b)