Tukey's Ladder of Powers

Conducts Tukey's Ladder of Powers on a vector of values to produce a more-normally distributed vector of values.

Usage

transformTukey(
  x,
  start = -10,
  end = 10,
  int = 0.025,
  plotit = TRUE,
  verbose = FALSE,
  quiet = FALSE,
  statistic = 1,
  returnLambda = FALSE
)

Arguments

x

A vector of values.

start

The starting value of lambda to try.

end

The ending value of lambda to try.

int

The interval between lambda values to try.

plotit

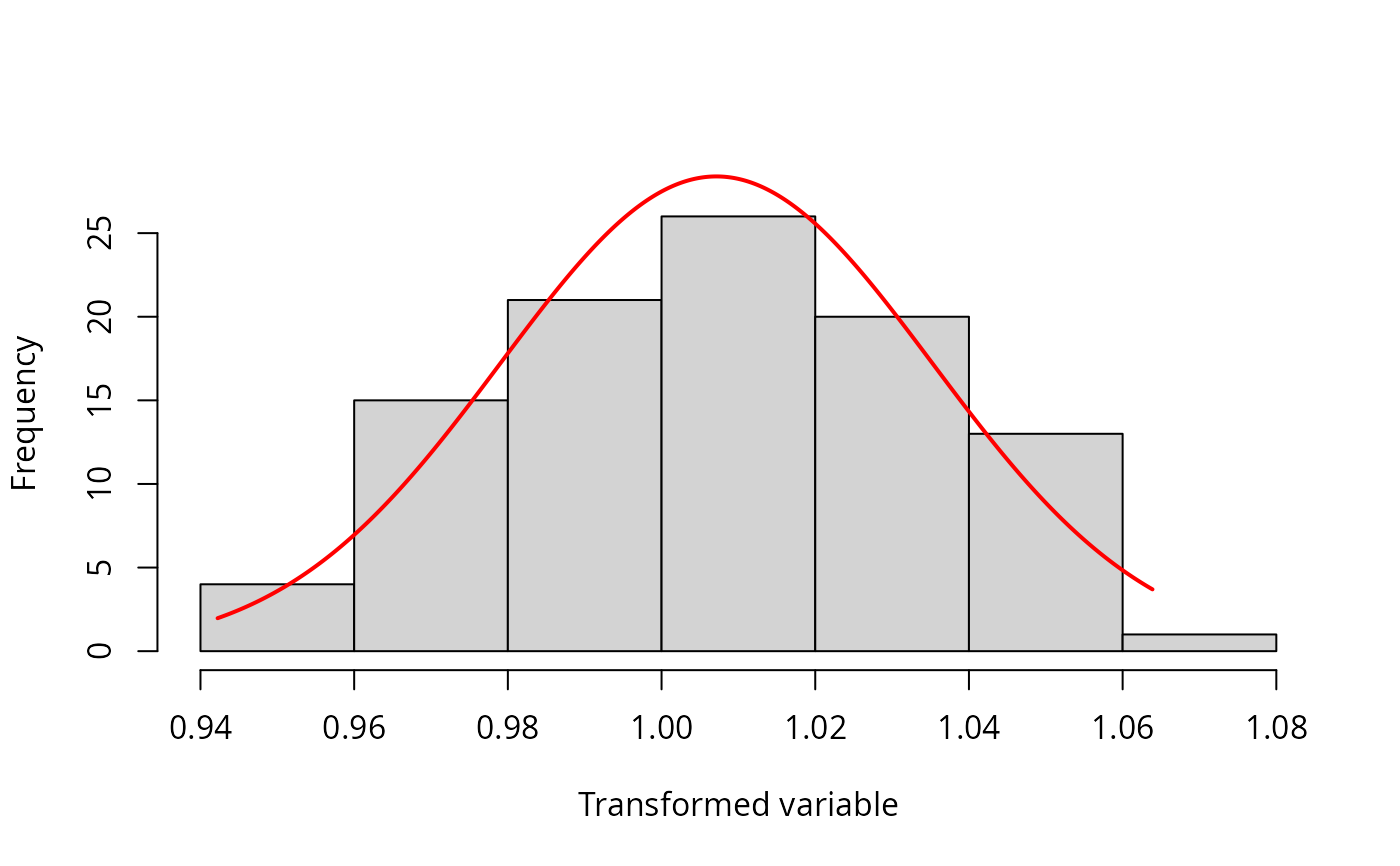
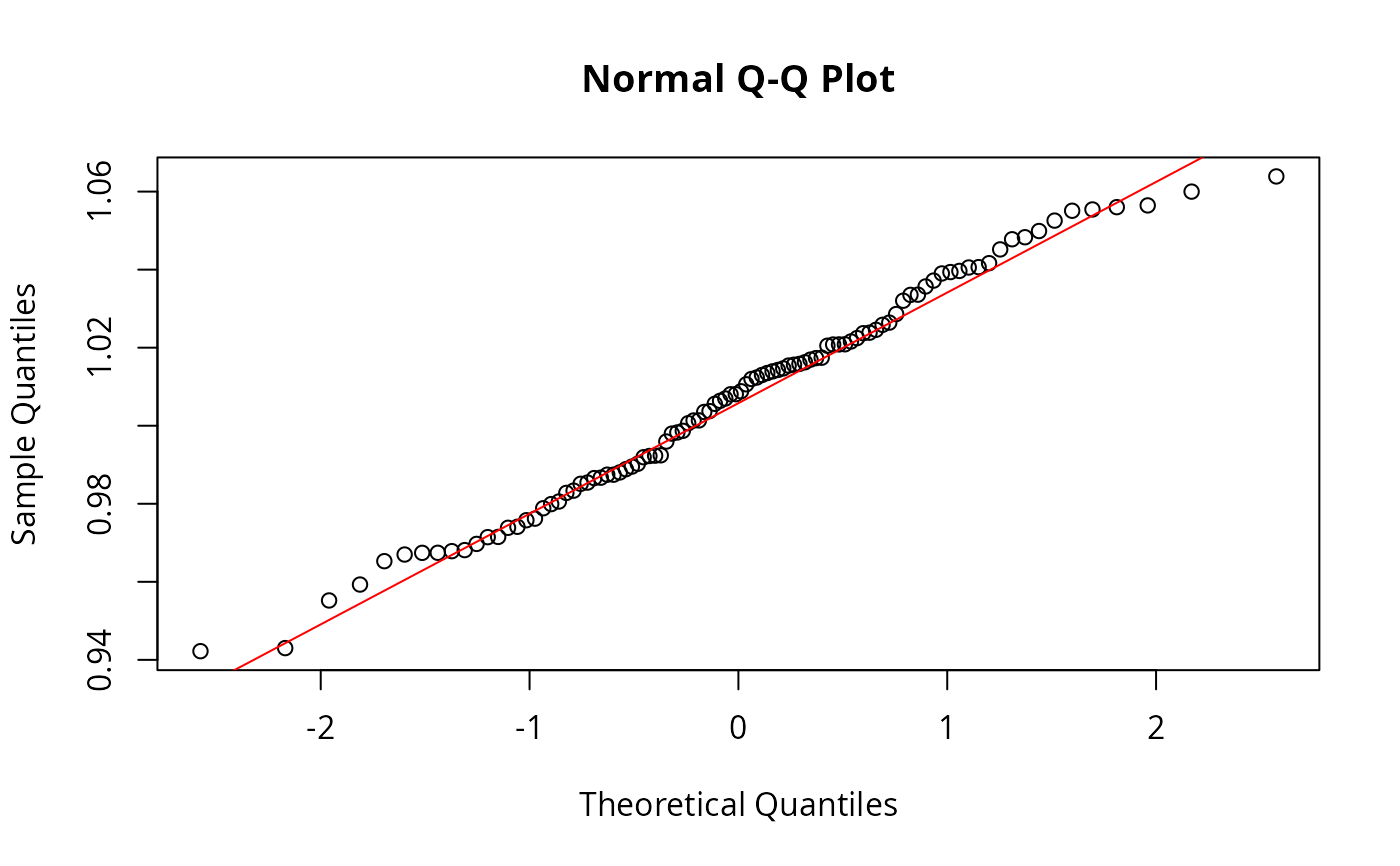
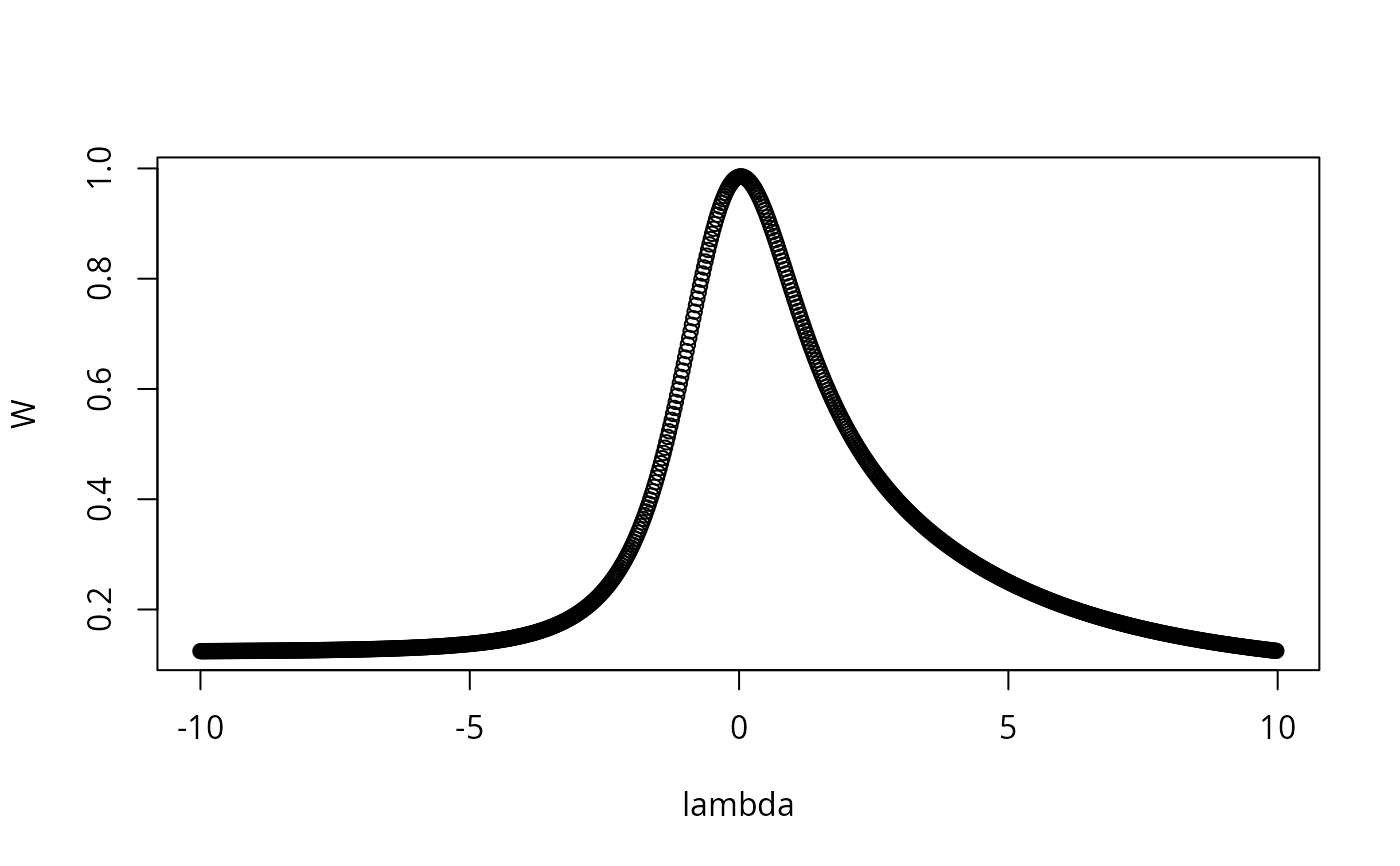
If TRUE, produces plots of Shapiro-Wilks W or Anderson-Darling A vs. lambda, a histogram of transformed values, and a quantile-quantile plot of transformed values.

verbose

If TRUE, prints extra output for Shapiro-Wilks W or Anderson-Darling A vs. lambda.

quiet

If TRUE, doesn't print any output to the screen.

statistic

If 1, uses Shapiro-Wilks test. Will report NA if the sample size is greater than 5000. If 2, uses Anderson-Darling test.

returnLambda

If TRUE, returns only the lambda value, not the vector of transformed values.

Value

The transformed vector of values. The chosen lambda value is printed directly.

Details

The function simply loops through lamdba values from start to end at an interval of int.

The function then chooses the lambda which maximizes the Shapiro-Wilks W statistic or minimizes the Anderson-Darling A statistic.

It may be beneficial to add a constant to the input vector so that all values are posititive. For left-skewed data, a (Constant - X) transformation may be helpful. Large values may need to be scaled.

References

https://rcompanion.org/handbook/I_12.html

Author

Salvatore Mangiafico, mangiafico@njaes.rutgers.edu

Examples

### Log-normal distribution example
Conc = rlnorm(100)
Conc.trans = transformTukey(Conc)

#> 
#>     lambda      W Shapiro.p.value
#> 402  0.025 0.9855          0.3452
#> 
#> if (lambda >  0){TRANS = x ^ lambda} 
#> if (lambda == 0){TRANS = log(x)} 
#> if (lambda <  0){TRANS = -1 * x ^ lambda} 
#>