Numerical Derivatives of (x,y) Data via Smoothing Splines

Compute numerical derivatives of \(f()\) given observations (x,y), using cubic smoothing splines with GCV, see smooth.spline. In other words, estimate \(f'()\) and/or \(f''()\) for the model $$Y_i = f(x_i) + E_i, \ \ i = 1,\dots n,$$

D1D2(x, y, xout = x, spar.offset = 0.1384, deriv = 1:2, spl.spar = NULL)

Arguments

x,y

numeric vectors of same length, supposedly from a model y ~ f(x).

xout

abscissa values at which to evaluate the derivatives.

spar.offset

numeric fudge added to the smoothing parameter, see spl.par below.

deriv

integer in 1:2 indicating which derivatives are to be computed.

spl.spar

direct smoothing parameter for smooth.spline. If it is NULL (as per default), the smoothing parameter used will be spar.offset + sp$spar, where sp$spar is the GCV estimated smoothing parameter, see smooth.spline.

Details

It is well known that for derivative estimation, the optimal smoothing parameter is larger (more smoothing) than for the function itself. spar.offset is really just a fudge offset added to the smoothing parameter. Note that in R's implementation of smooth.spline, spar is really on the \(\log\lambda\) scale.

When deriv = 1:2 (as per default), both derivatives are estimated with the same smoothing parameter which is suboptimal for the single functions individually. Another possibility is to call D1D2(*, deriv = k) twice with k = 1 and k = 2 and use a larger smoothing parameter for the second derivative.

Value

a list with several components,

x

the abscissae values at which the derivative(s) are evaluated.

D1

if deriv contains 1, estimated values of \(f'(x_i)\) where \(x_i\) are the values from xout.

D2

if deriv contains 2, estimated values of \(f''(x_i)\).

spar

the smoothing parameter used in the (final) smooth.spline call.

df

the equivalent degrees of freedom in that smooth.spline call.

Author

Martin Maechler, in 1992 (for S).

See also

D2ss which calls smooth.spline twice, first on y, then on the \(f'(x_i)\) values; smooth.spline on which it relies completely.

Examples

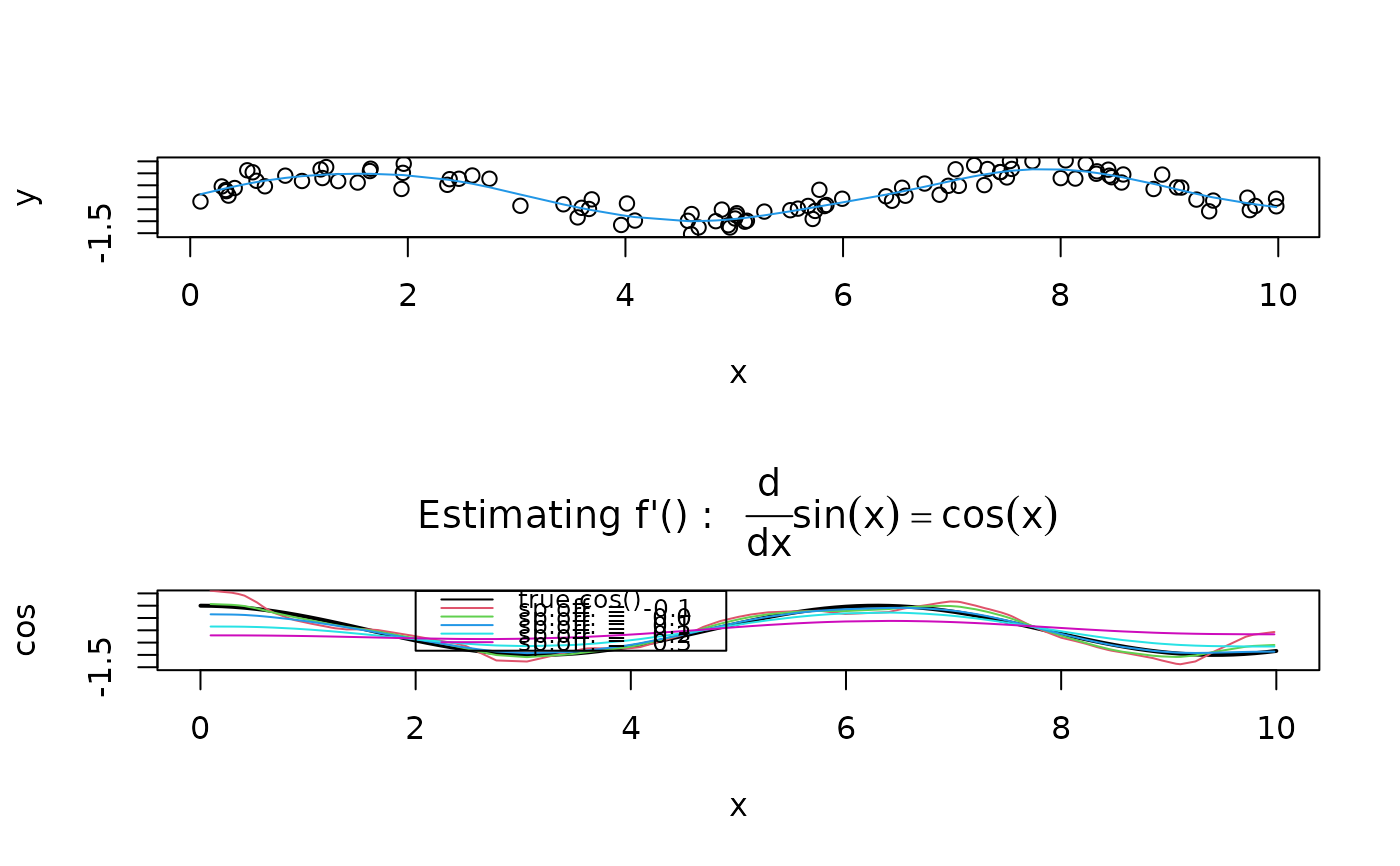
 set.seed(8840)
 x <- runif(100, 0,10)
 y <- sin(x) + rnorm(100)/4

 op <- par(mfrow = c(2,1))
 plot(x,y)
 lines(ss <- smooth.spline(x,y), col = 4)
 str(ss[c("df", "spar")])
#> List of 2
#>  $ df  : num 10.3
#>  $ spar: num 0.716
 plot(cos, 0, 10, ylim = c(-1.5,1.5), lwd=2,
      main = expression("Estimating f'() : "~~ frac(d,dx) * sin(x) == cos(x)))
 offs <- c(-0.1, 0, 0.1, 0.2, 0.3)
 i <- 1
 for(off in offs) {
   d12 <- D1D2(x,y, spar.offset = off)
   lines(d12$x, d12$D1, col = i <- i+1)
 }
 legend(2,1.6, c("true cos()",paste("sp.off. = ", format(offs))), lwd=1,
        col = 1:(1+length(offs)), cex = 0.8, bg = NA)

 par(op)