Diagonal Discriminant Analysis
diagDA.RdThis function implements a simple Gaussian maximum likelihood discriminant rule, for diagonal class covariance matrices.
In machine learning lingo, this is called “Naive Bayes” (for continuous predictors). Note that naive Bayes is more general, as it models discrete predictors as multinomial, i.e., binary predictor variables as Binomial / Bernoulli.
Arguments
- x,ls
learning set data matrix, with rows corresponding to cases (e.g., mRNA samples) and columns to predictor variables (e.g., genes).
- cll
class labels for learning set, must be consecutive integers.
- object
object of class
dDA.- ts, newdata
test set (prediction) data matrix, with rows corresponding to cases and columns to predictor variables.
- pool
logical flag. If true (by default), the covariance matrices are assumed to be constant across classes and the discriminant rule is linear in the data. Otherwise (
pool= FALSE), the covariance matrices may vary across classes and the discriminant rule is quadratic in the data.- ...
further arguments passed to and from methods.
Value
dDA() returns an object of class dDA for which there are
print and predict methods. The latter
returns the same as diagDA():
diagDA() returns an integer vector of class predictions for the
test set.
References
S. Dudoit, J. Fridlyand, and T. P. Speed. (2000) Comparison of Discrimination Methods for the Classification of Tumors Using Gene Expression Data. (Statistics, UC Berkeley, June 2000, Tech Report #576)
Examples
## two artificial examples by Andreas Greutert:
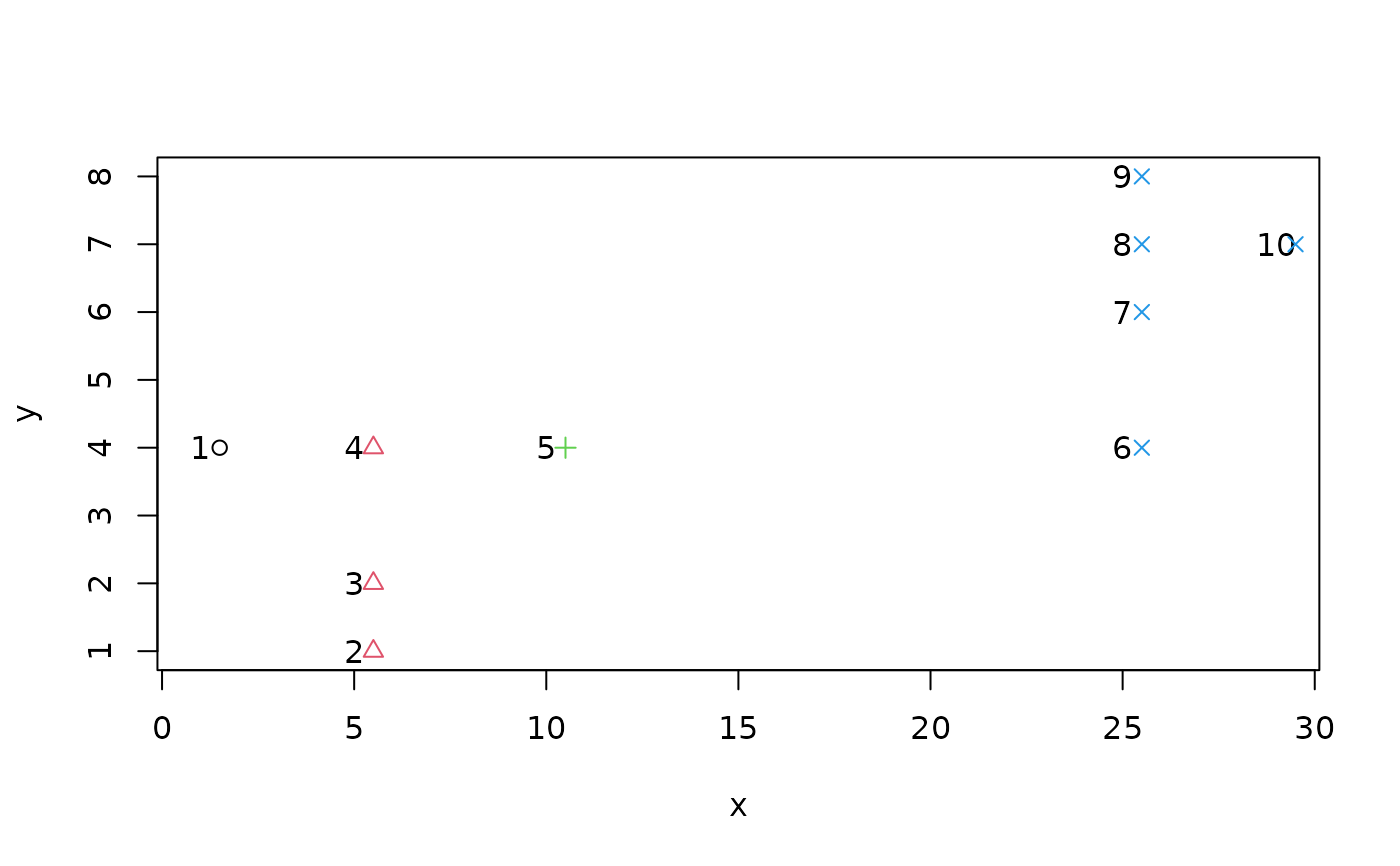
d1 <- data.frame(x = c(1, 5, 5, 5, 10, 25, 25, 25, 25, 29),
y = c(4, 1, 2, 4, 4, 4, 6:8, 7))
n.plot(d1)
library(cluster)
(cl1P <- pam(d1,k=4)$cluster) # 4 surprising clusters
#> [1] 1 2 2 2 3 4 4 4 4 4
with(d1, points(x+0.5, y, col = cl1P, pch =cl1P))
 i1 <- c(1,3,5,6)
tr1 <- d1[-i1,]
cl1. <- c(1,2,1,2,1,3)
cl1 <- c(2,2,1,1,1,3)
plot(tr1, cex=2, col = cl1, pch = 20+cl1)
(dd.<- diagDA(tr1, cl1., ts = d1[ i1,]))# ok
#> [1] 2 2 2 1
(dd <- diagDA(tr1, cl1 , ts = d1[ i1,]))# ok, too!
#> [1] 2 2 2 1
points(d1[ i1,], pch = 10, cex=3, col = dd)
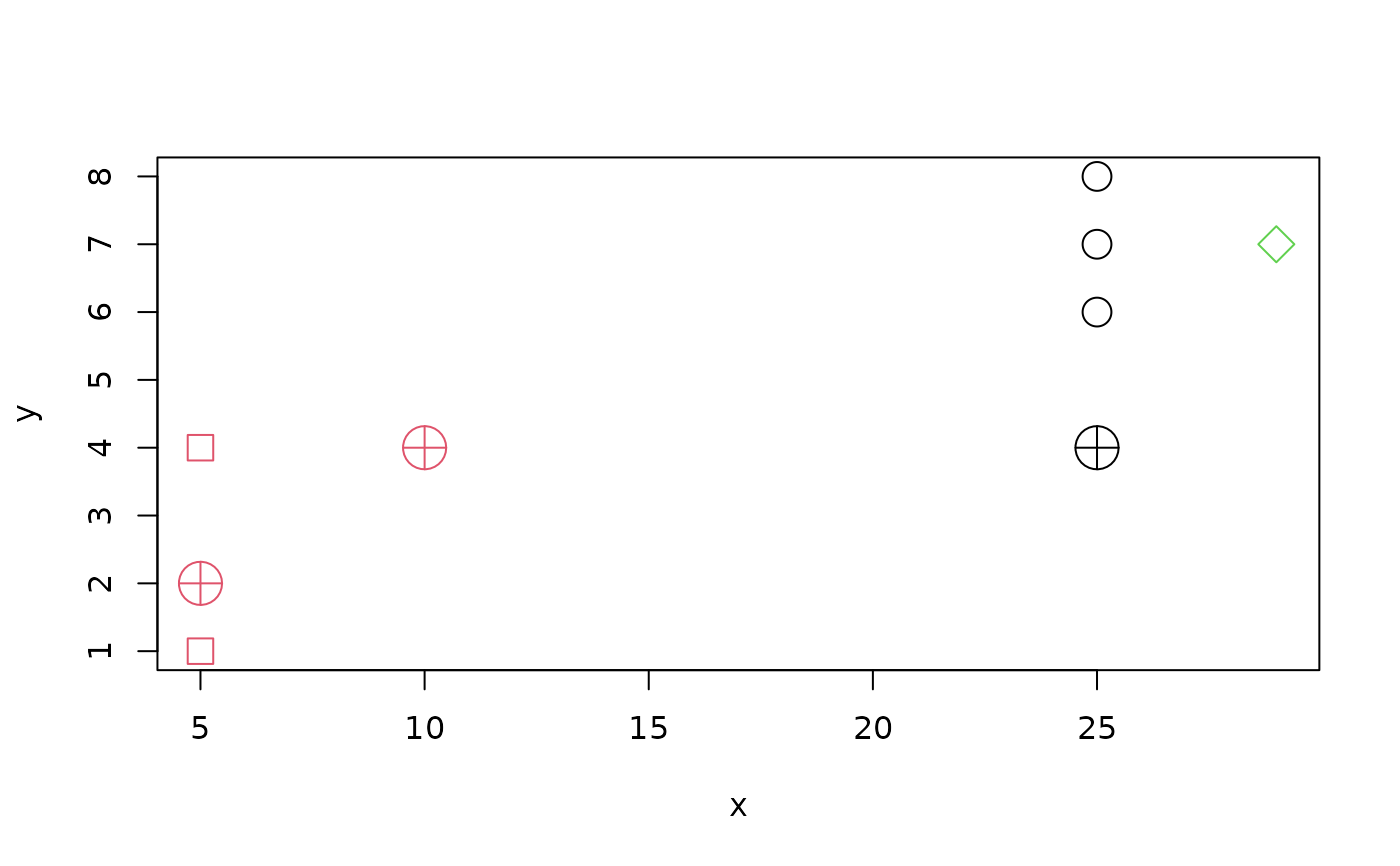
i1 <- c(1,3,5,6)
tr1 <- d1[-i1,]
cl1. <- c(1,2,1,2,1,3)
cl1 <- c(2,2,1,1,1,3)
plot(tr1, cex=2, col = cl1, pch = 20+cl1)
(dd.<- diagDA(tr1, cl1., ts = d1[ i1,]))# ok
#> [1] 2 2 2 1
(dd <- diagDA(tr1, cl1 , ts = d1[ i1,]))# ok, too!
#> [1] 2 2 2 1
points(d1[ i1,], pch = 10, cex=3, col = dd)
 ## use new fit + predict instead :
(r1 <- dDA(tr1, cl1))
#> Linear (pooled var) Diagonal Discriminant Analysis,
#> dDA(x = tr1, cll = cl1)
#> (n= 6) x (p= 2) data in K=3 classes of [3, 2, 1] observations each
#>
(r1.<- dDA(tr1, cl1.))
#> Linear (pooled var) Diagonal Discriminant Analysis,
#> dDA(x = tr1, cll = cl1.)
#> (n= 6) x (p= 2) data in K=3 classes of [3, 2, 1] observations each
#>
stopifnot(dd == predict(r1, new = d1[ i1,]),
dd.== predict(r1., new = d1[ i1,]))
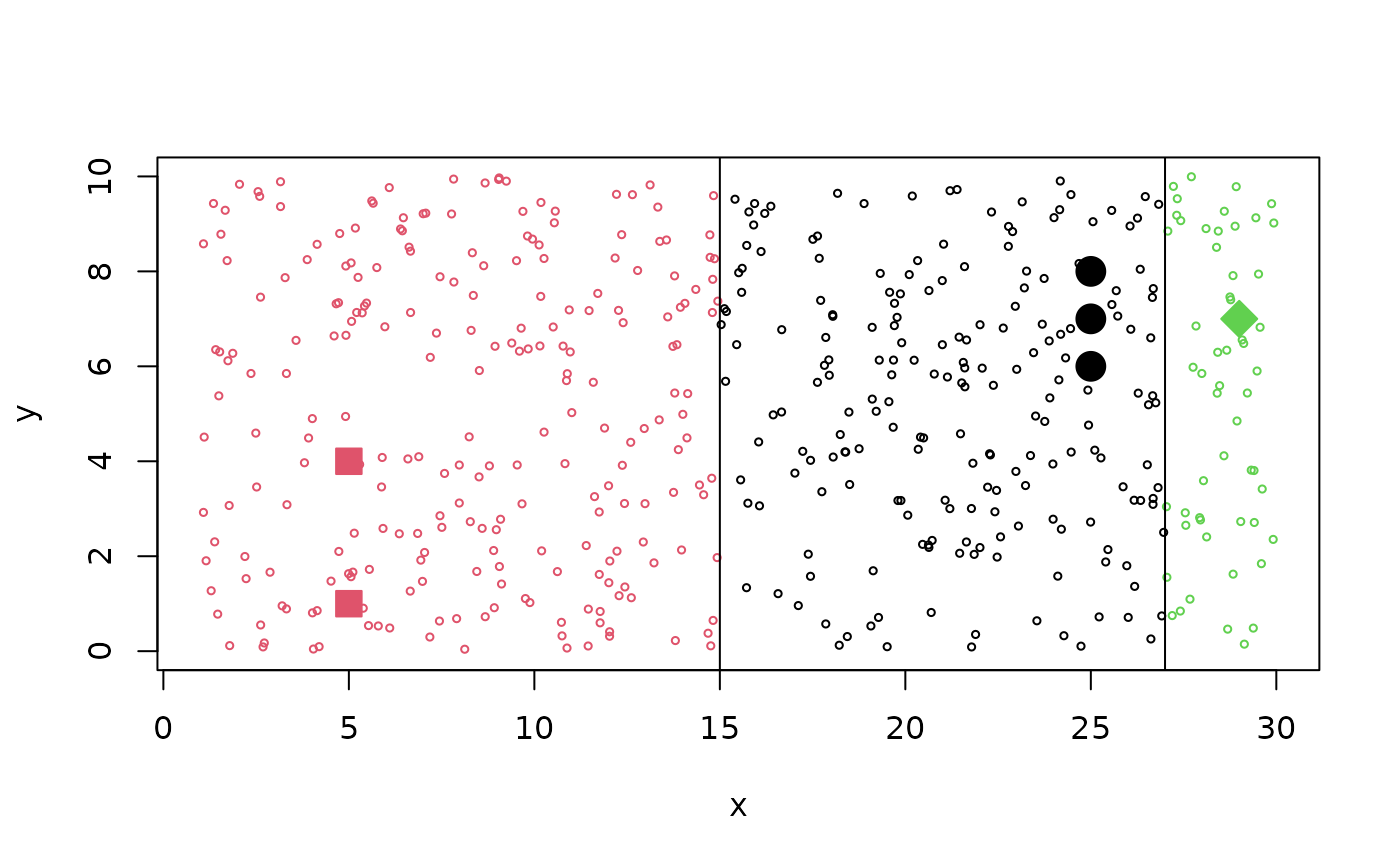
plot(tr1, cex=2, col = cl1, bg = cl1, pch = 20+cl1,
xlim=c(1,30), ylim= c(0,10))
xy <- cbind(x= runif(500, min=1,max=30), y = runif(500, min=0, max=10))
points(xy, cex= 0.5, col = predict(r1, new = xy))
abline(v=c( mean(c(5,25)), mean(c(25,29))))
## use new fit + predict instead :
(r1 <- dDA(tr1, cl1))
#> Linear (pooled var) Diagonal Discriminant Analysis,
#> dDA(x = tr1, cll = cl1)
#> (n= 6) x (p= 2) data in K=3 classes of [3, 2, 1] observations each
#>
(r1.<- dDA(tr1, cl1.))
#> Linear (pooled var) Diagonal Discriminant Analysis,
#> dDA(x = tr1, cll = cl1.)
#> (n= 6) x (p= 2) data in K=3 classes of [3, 2, 1] observations each
#>
stopifnot(dd == predict(r1, new = d1[ i1,]),
dd.== predict(r1., new = d1[ i1,]))
plot(tr1, cex=2, col = cl1, bg = cl1, pch = 20+cl1,
xlim=c(1,30), ylim= c(0,10))
xy <- cbind(x= runif(500, min=1,max=30), y = runif(500, min=0, max=10))
points(xy, cex= 0.5, col = predict(r1, new = xy))
abline(v=c( mean(c(5,25)), mean(c(25,29))))
 ## example where one variable xj has Var(xj) = 0:
x4 <- matrix(c(2:4,7, 6,8,5,6, 7,2,3,1, 7,7,7,7), ncol=4)
y <- c(2,2, 1,1)
m4.1 <- dDA(x4, y, pool = FALSE)
m4.2 <- dDA(x4, y, pool = TRUE)
xx <- matrix(c(3,7,5,7), ncol=4)
predict(m4.1, xx)## gave integer(0) previously
#> [1] 2
predict(m4.2, xx)
#> [1] 2
## example where one variable xj has Var(xj) = 0:
x4 <- matrix(c(2:4,7, 6,8,5,6, 7,2,3,1, 7,7,7,7), ncol=4)
y <- c(2,2, 1,1)
m4.1 <- dDA(x4, y, pool = FALSE)
m4.2 <- dDA(x4, y, pool = TRUE)
xx <- matrix(c(3,7,5,7), ncol=4)
predict(m4.1, xx)## gave integer(0) previously
#> [1] 2
predict(m4.2, xx)
#> [1] 2