Generate Sequence Iterating a Linear Recursion

Generate numeric sequences applying a linear recursion nr.it times.

iterate.lin.recursion(x, coeff, delta = 0, nr.it)

Arguments

x

numeric vector with initial values, i.e., specifying the beginning of the resulting sequence; must be of length (larger or) equal to length(coeff).

coeff

coefficient vector of the linear recursion.

delta

numeric scalar added to each term; defaults to 0. If not zero, determines the linear drift component.

nr.it

integer, number of iterations.

Value

numeric vector, say r, of length n + nr.it, where n = length(x). Initialized as r[1:n] = x, the recursion is r[k+1] = sum(coeff * r[(k-m+1):k]), where m = length(coeff).

Note

Depending on the zeroes of the characteristic polynomial of coeff, there are three cases, of convergence, oszillation and divergence.

Author

Martin Maechler

See also

seq can be regarded as a trivial special case.

Examples

## The Fibonacci sequence:
iterate.lin.recursion(0:1, c(1,1), nr = 12)
#>  [1]   0   1   1   2   3   5   8  13  21  34  55  89 144 233
## 0 1 1 2 3 5 8 13 21 34 55 89 144 233

## seq() as a special case:
stopifnot(iterate.lin.recursion(4,1, d=2, nr=20)
          == seq(4, by=2, length=1+20))

## ''Deterministic AR(2)'' :
round(iterate.lin.recursion(1:4, c(-0.7, 0.9), d = 2, nr=15), dig=3)
#>  [1] 1.000 2.000 3.000 4.000 3.500 2.350 1.665 1.854 2.503 2.955 2.908 2.548
#> [13] 2.258 2.249 2.443 2.625 2.652 2.550 2.438
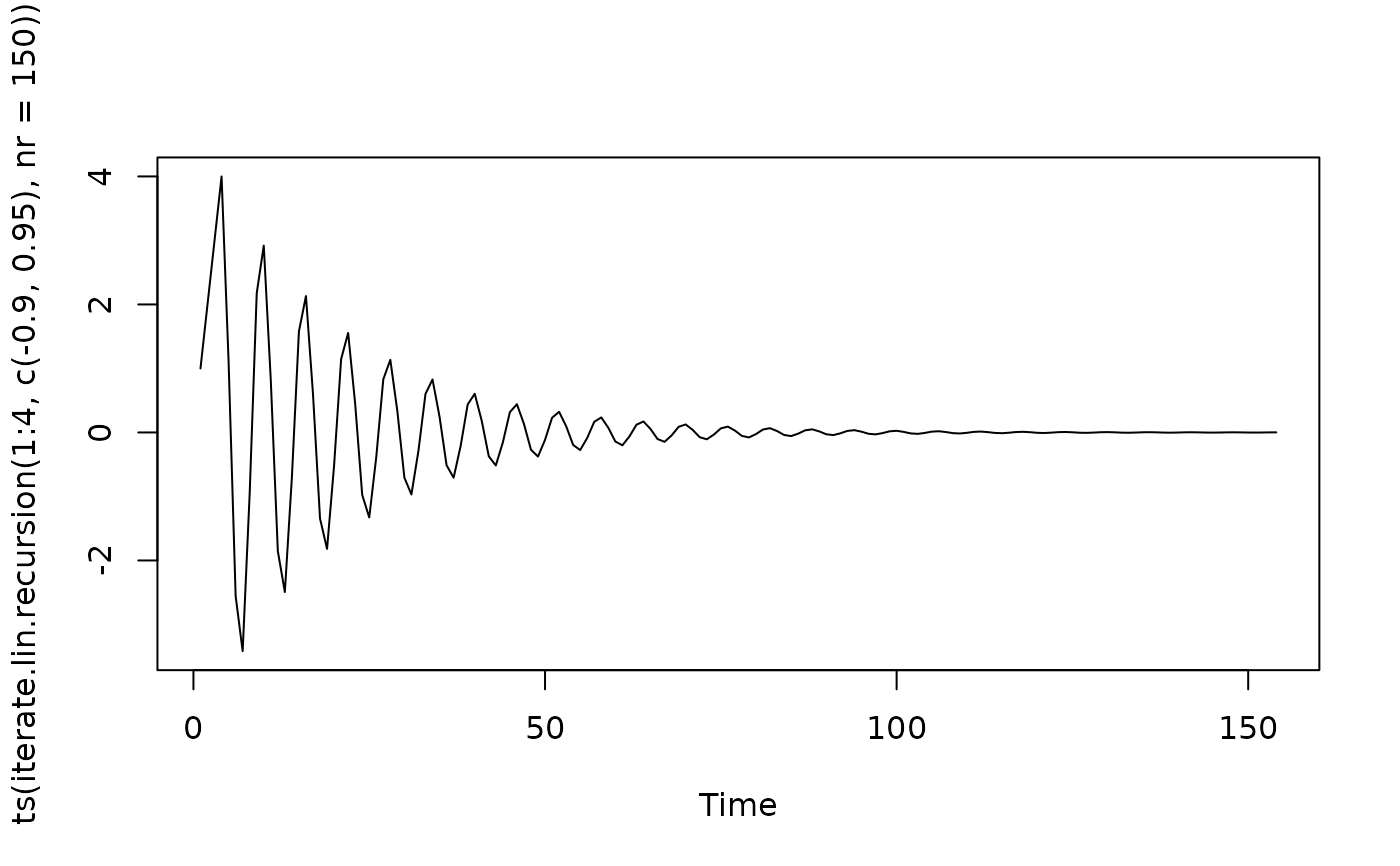
## slowly decaying :
plot(ts(iterate.lin.recursion(1:4, c(-0.9, 0.95), nr=150)))