Enhance Formula by Wrapping each Term, e.g., by "s(.)"

The main motivation for this function has been the easy construction of a “full GAM formula” from something as simple as Y ~ ..
The potential use is slightly more general.

wrapFormula(f, data, wrapString = "s(*)")

Arguments

f

the initial formula; typically something like Y ~ ..

data

data.frame to which the formula applies; see, formula or also gam or lm.

wrapString

character string, containing "*", specifying the wrapping expression to use.

Value

a formula very similar to f; just replacing each additive term by its wrapped version.

Note

There are limits for this to work correctly; notably the right hand side of the formula f should not be nested or otherwise complicated, rather typically just . as in the examples.

Author

Martin Maechler, May 2007.

See also

formula; gam from package mgcv (or also from package gam).

Examples

myF <- wrapFormula(Fertility ~ . , data = swiss)
myF # Fertility ~ s(Agriculture) + s(....) + ...
#> Fertility ~ s(Agriculture) + s(Examination) + s(Education) + 
#>     s(Catholic) + s(Infant.Mortality)
#> <environment: 0x55faa17379c0>

if(require("mgcv")) {
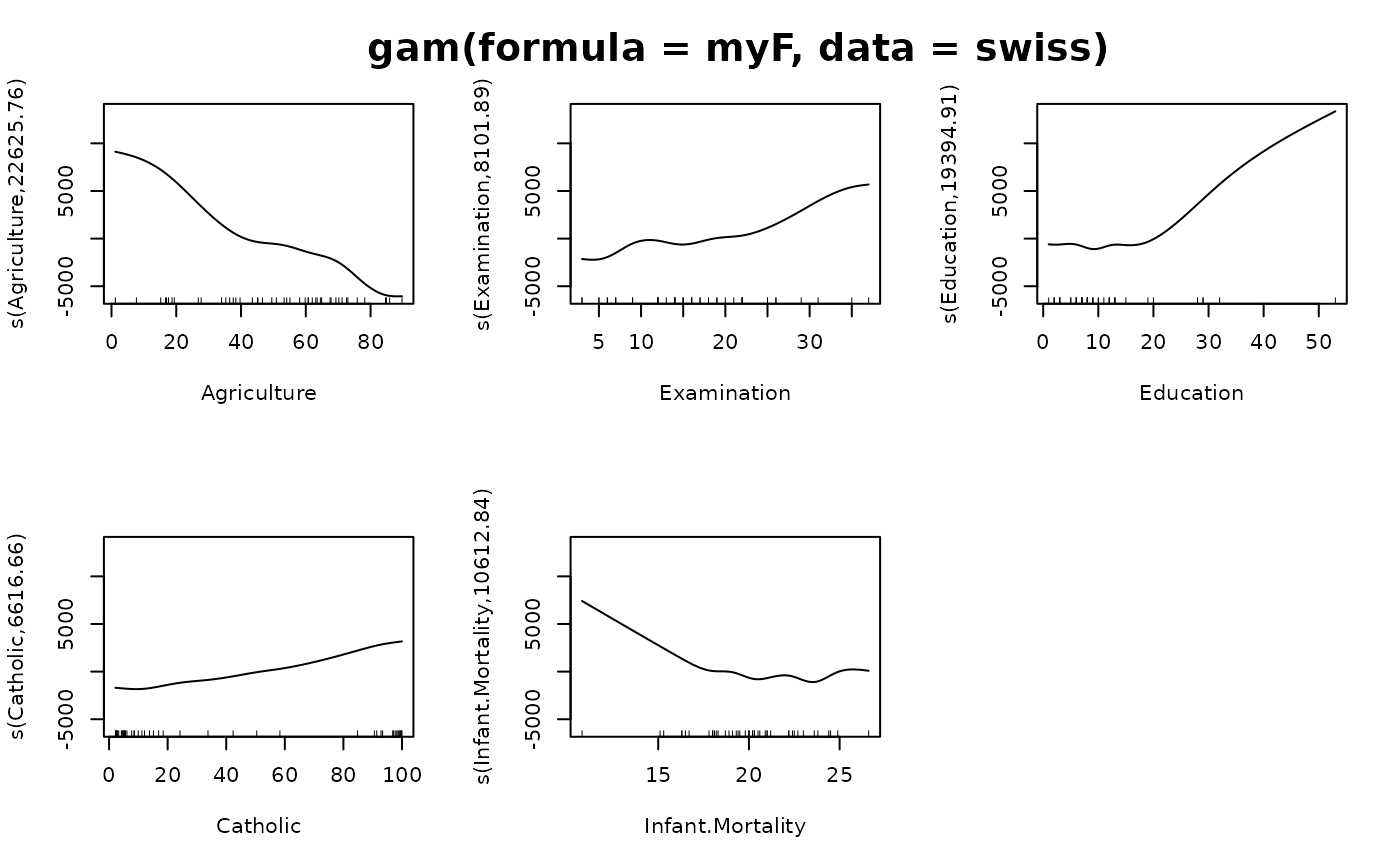
   m1 <- gam(myF, data = swiss)
   print( summary(m1) )
   plot(m1, pages = 1) ; title(format(m1$call), line= 2.5)
}
#> Loading required package: mgcv
#> Loading required package: nlme
#> This is mgcv 1.9-1. For overview type 'help("mgcv-package")'.
#> Warning: NaNs produced
#> Warning: NaNs produced
#> Warning: NaNs produced
#> Warning: NaNs produced
#> Warning: NaNs produced
#> 
#> Family: gaussian 
#> Link function: identity 
#> 
#> Formula:
#> Fertility ~ s(Agriculture) + s(Examination) + s(Education) + 
#>     s(Catholic) + s(Infant.Mortality)
#> 
#> Parametric coefficients:
#>             Estimate Std. Error t value Pr(>|t|)
#> (Intercept)     75.4        NaN     NaN      NaN
#> 
#> Approximate significance of smooth terms:
#>                       edf Ref.df   F p-value
#> s(Agriculture)      22626      0 NaN     NaN
#> s(Examination)       8102      0 NaN     NaN
#> s(Education)        19395      0 NaN     NaN
#> s(Catholic)          6617      0 NaN     NaN
#> s(Infant.Mortality) 10613      0 NaN     NaN
#> 
#> R-sq.(adj) =    194   Deviance explained = -2.83e+07%
#> GCV = 1.1432e+06  Scale est. = -1.475e+06  n = 47
#> Warning: No variance estimates available


## other wrappers:
wrapFormula(Fertility ~ . , data = swiss, wrap = "lo(*)")
#> Fertility ~ lo(Agriculture) + lo(Examination) + lo(Education) + 
#>     lo(Catholic) + lo(Infant.Mortality)
#> <environment: 0x55faa17379c0>
wrapFormula(Fertility ~ . , data = swiss, wrap = "poly(*, 4)")
#> Fertility ~ poly(Agriculture, 4) + poly(Examination, 4) + poly(Education, 
#>     4) + poly(Catholic, 4) + poly(Infant.Mortality, 4)
#> <environment: 0x55faa17379c0>