M-Spline Basis for Polynomial Splines

Generates the basis matrix of regular M-spline, periodic M-spline, and the corresponding integrals and derivatives.

mSpline(
  x,
  df = NULL,
  knots = NULL,
  degree = 3L,
  intercept = FALSE,
  Boundary.knots = NULL,
  periodic = FALSE,
  derivs = 0L,
  integral = FALSE,
  warn.outside = getOption("splines2.warn.outside", TRUE),
  ...
)

msp(
  x,
  df = NULL,
  knots = NULL,
  degree = 3L,
  intercept = FALSE,
  Boundary.knots = NULL,
  periodic = FALSE,
  derivs = 0L,
  integral = FALSE,
  warn.outside = getOption("splines2.warn.outside", TRUE),
  ...
)

Arguments

x: The predictor variable. Missing values are allowed and will be returned as they are.
df: Degree of freedom that equals to the column number of the returned matrix. One can specify df rather than knots, then the function chooses df - degree - as.integer(intercept) internal knots at suitable quantiles of x ignoring missing values and those x outside of the boundary. For periodic splines, df - as.integer(intercept) internal knots will be chosen at suitable quantiles of x relative to the beginning of the cyclic intervals they belong to (see Examples) and the number of internal knots must be greater or equal to the specified degree - 1. If internal knots are specified via knots, the specified df will be ignored.
knots: The internal breakpoints that define the splines. The default is NULL, which results in a basis for ordinary polynomial regression. Typical values are the mean or median for one knot, quantiles for more knots. For periodic splines, the number of knots must be greater or equal to the specified degree - 1. Duplicated internal knots are not allowed.
degree: A nonnegative integer specifying the degree of the piecewise polynomial. The default value is 3 for cubic splines. Zero degree is allowed for piecewise constant basis functions.
intercept: If TRUE, the complete basis matrix will be returned. Otherwise, the first basis will be excluded from the output.
Boundary.knots: Boundary points at which to anchor the splines. By default, they are the range of x excluding NA. If both knots and Boundary.knots are supplied, the basis parameters do not depend on x. Data can extend beyond Boundary.knots. For periodic splines, the specified bounary knots define the cyclic interval.
periodic: A logical value. If TRUE, the periodic splines will be returned. The default value is FALSE.
derivs: A nonnegative integer specifying the order of derivatives of splines basis function. The default value is 0.
integral: A logical value. If TRUE, the corresponding integrals of spline basis functions will be returned. The default value is FALSE. For periodic splines, the integral of each basis is integrated from the left boundary knot.
warn.outside: A logical value indicating if a warning should be thrown out when any x is outside the boundary. This option can also be set through options("splines2.warn.outside") after the package is loaded.
...: Optional arguments that are not used.

Value

A numeric matrix of length(x) rows and df columns if df is specified. If knots are specified instead, the output matrix will consist of length(knots) + degree + as.integer(intercept) columns if periodic = FALSE, or length(knots) + as.integer(intercept) columns if periodic = TRUE. Attributes that correspond to the arguments specified are returned for usage of other functions in this package.

Details

This function contains an implementation of the closed-form M-spline basis based on the recursion formula given by Ramsay (1988) or periodic M-spline basis following the procedure producing periodic B-splines given in Piegl and Tiller (1997). For monotone regression, one can use I-splines (see iSpline) instead of M-splines. For shape-restricted regression, see Wang and Yan (2021) for examples.

The function msp() is an alias of to encourage the use in a model formula.

References

Ramsay, J. O. (1988). Monotone regression splines in action. Statistical science, 3(4), 425–441.

Piegl, L., & Tiller, W. (1997). The NURBS book. Springer Science & Business Media.

Wang, W., & Yan, J. (2021). Shape-restricted regression splines with R package splines2. Journal of Data Science, 19(3),498–517.

Examples

library(splines2)

### example given in the reference paper by Ramsay (1988)
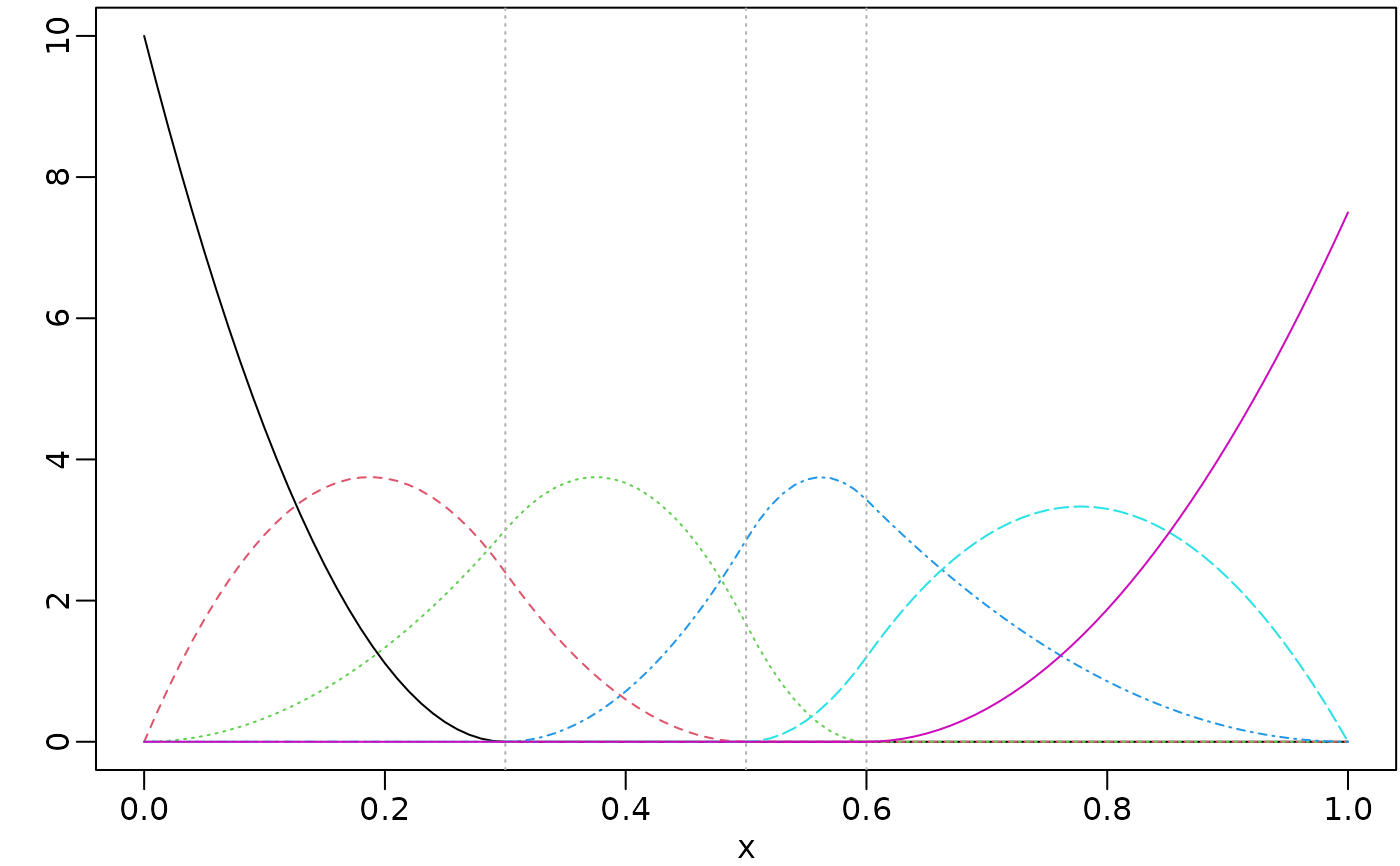
x <- seq.int(0, 1, 0.01)
knots <- c(0.3, 0.5, 0.6)
msMat <- mSpline(x, knots = knots, degree = 2, intercept = TRUE)

op <- par(mar = c(2.5, 2.5, 0.2, 0.1), mgp = c(1.5, 0.5, 0))
plot(msMat, mark_knots = "internal")


## derivatives of M-splines
dmsMat <- mSpline(x, knots = knots, degree = 2,
                  intercept = TRUE, derivs = 1)

## or using the deriv method
dmsMat1 <- deriv(msMat)
stopifnot(all.equal(dmsMat, dmsMat1, check.attributes = FALSE))

### periodic M-splines
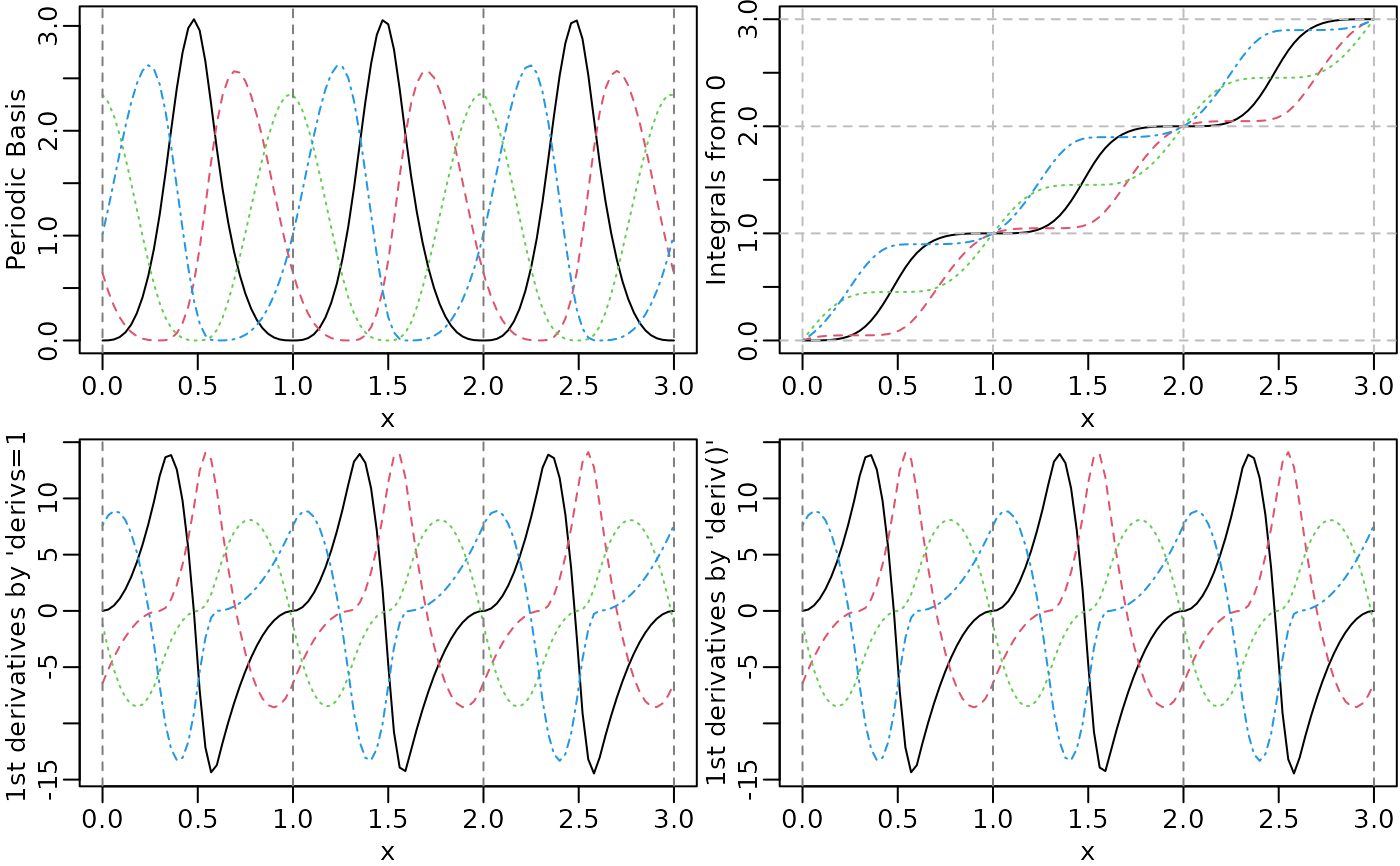
x <- seq.int(0, 3, 0.01)
bknots <- c(0, 1)
pMat <- mSpline(x, knots = knots, degree = 3, intercept = TRUE,
                Boundary.knots = bknots, periodic = TRUE)
## integrals
iMat <- mSpline(x, knots = knots, degree = 3, intercept = TRUE,
                Boundary.knots = bknots, periodic = TRUE, integral = TRUE)
## first derivatives by "derivs = 1"
dMat1 <- mSpline(x, knots = knots, degree = 3, intercept = TRUE,
                 Boundary.knots = bknots, periodic = TRUE, derivs = 1)
## first derivatives by using the deriv() method
dMat2 <- deriv(pMat)

par(mfrow = c(2, 2))
plot(pMat, ylab = "Periodic Basis", mark_knots = "boundary")
plot(iMat, ylab = "Integrals from 0")
abline(v = seq.int(0, max(x)), h = seq.int(0, max(x)), lty = 2, col = "grey")
plot(dMat1, ylab = "1st derivatives by 'derivs=1'", mark_knots = "boundary")
plot(dMat2, ylab = "1st derivatives by 'deriv()'", mark_knots = "boundary")

par(op) # reset to previous plotting settings

### default placement of internal knots for periodic splines
default_knots <- function(x, df, intercept = FALSE,
                        Boundary.knots = range(x, na.rm = TRUE)) {
    ## get x in the cyclic interval [0, 1)
    x2 <- (x - Boundary.knots[1]) %% (Boundary.knots[2] - Boundary.knots[1])
    knots <- quantile(x2, probs = seq(0, 1, length.out = df + 2 - intercept))
    unname(knots[- c(1, length(knots))])
}

df <- 8
degree <- 3
intercept <- TRUE
internal_knots <- default_knots(x, df, intercept)

## 1. specify df
spline_basis1 <- mSpline(x, degree = degree, df = df,
                         periodic = TRUE, intercept = intercept)
## 2. specify knots
spline_basis2 <- mSpline(x, degree = degree, knots = internal_knots,
                         periodic = TRUE, intercept = intercept)

all.equal(internal_knots, knots(spline_basis1))
#> [1] TRUE
all.equal(spline_basis1, spline_basis2)
#> [1] TRUE