Derivatives of the Incomplete Gamma Integral

The first two derivatives of the incomplete gamma integral.

pgamma.deriv(q, shape, tmax = 100)

Arguments

q, shape: As in pgamma but these must be vectors of positive values only and finite.

tmax: Maximum number of iterations allowed in the computation (per q value).

Details

Write $x = q$ and shape = $a$. The first and second derivatives with respect to $q$ and $a$ are returned. This function is similar in spirit to pgamma; define $$P(a,x) = \frac{1}{\Gamma(a)} \int_0^x t^{a-1} e^{-t} dt$$ so that $P(a, x)$ is pgamma(x, a). Currently a 6-column matrix is returned (in the future this may change and an argument may be supplied so that only what is required by the user is computed.)

The computations use a series expansion for $a \leq x \leq 1$ or or $x < a$, else otherwise a continued fraction expansion. Machine overflow can occur for large values of $x$ when $x$ is much greater than $a$.

Value

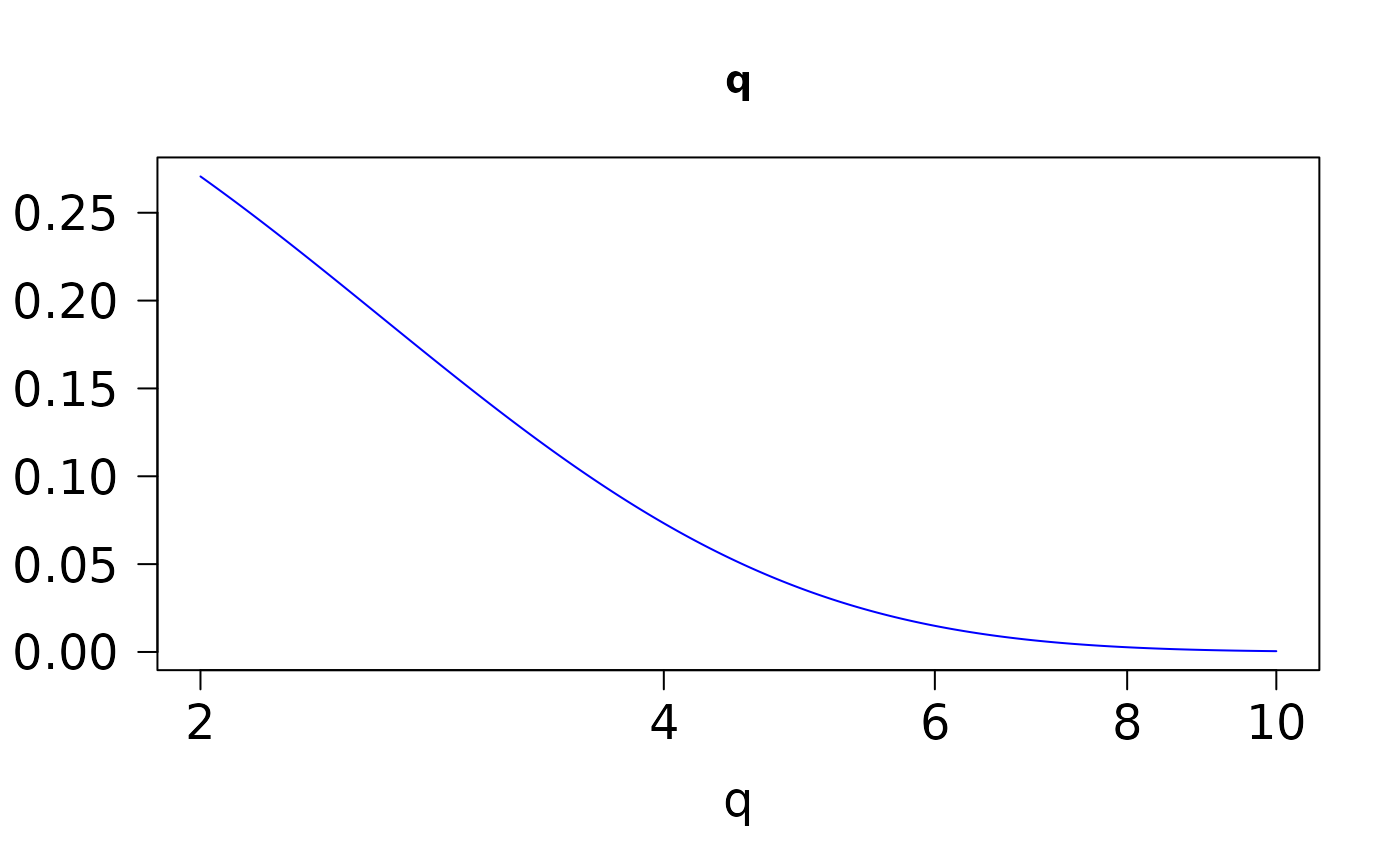
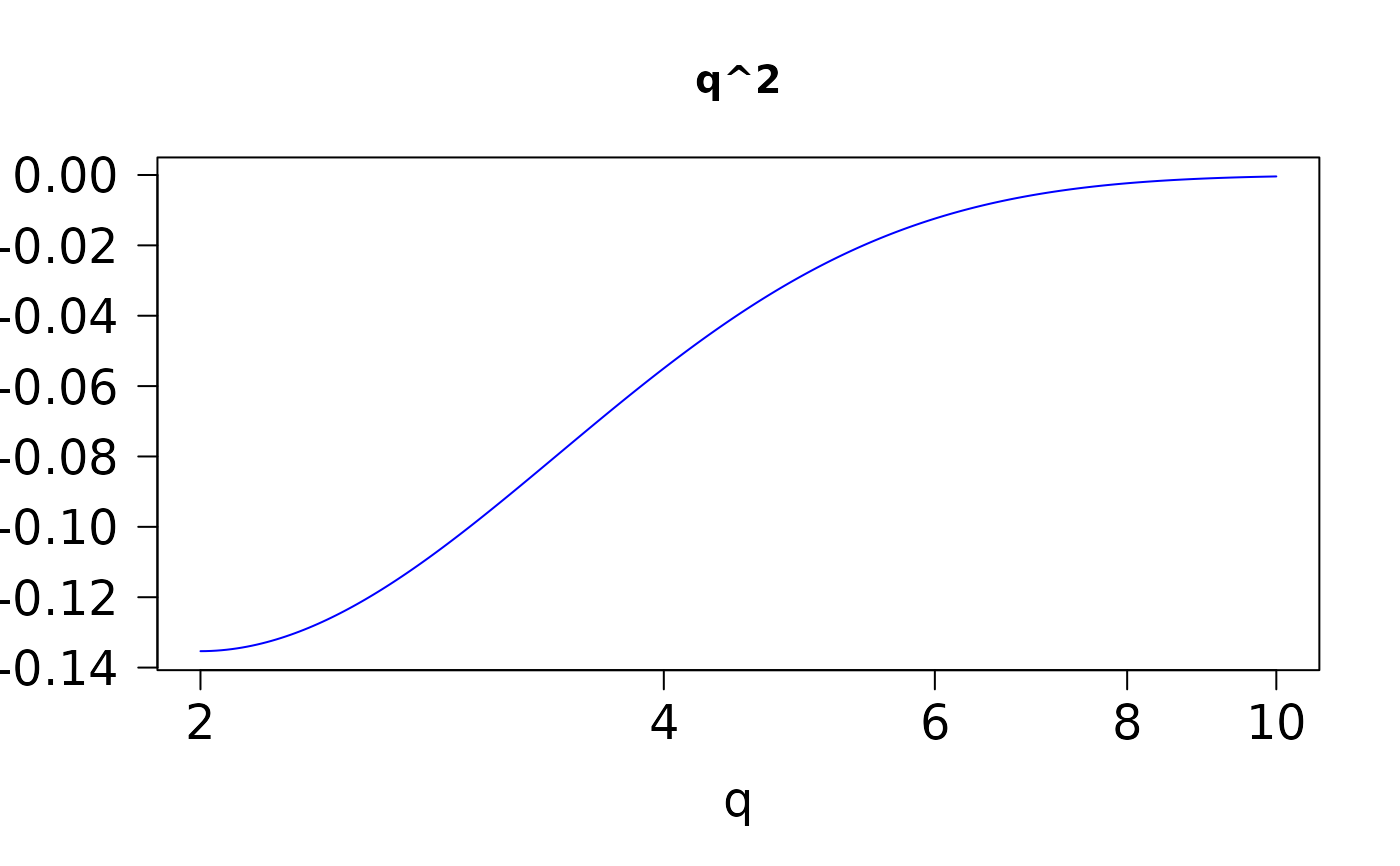
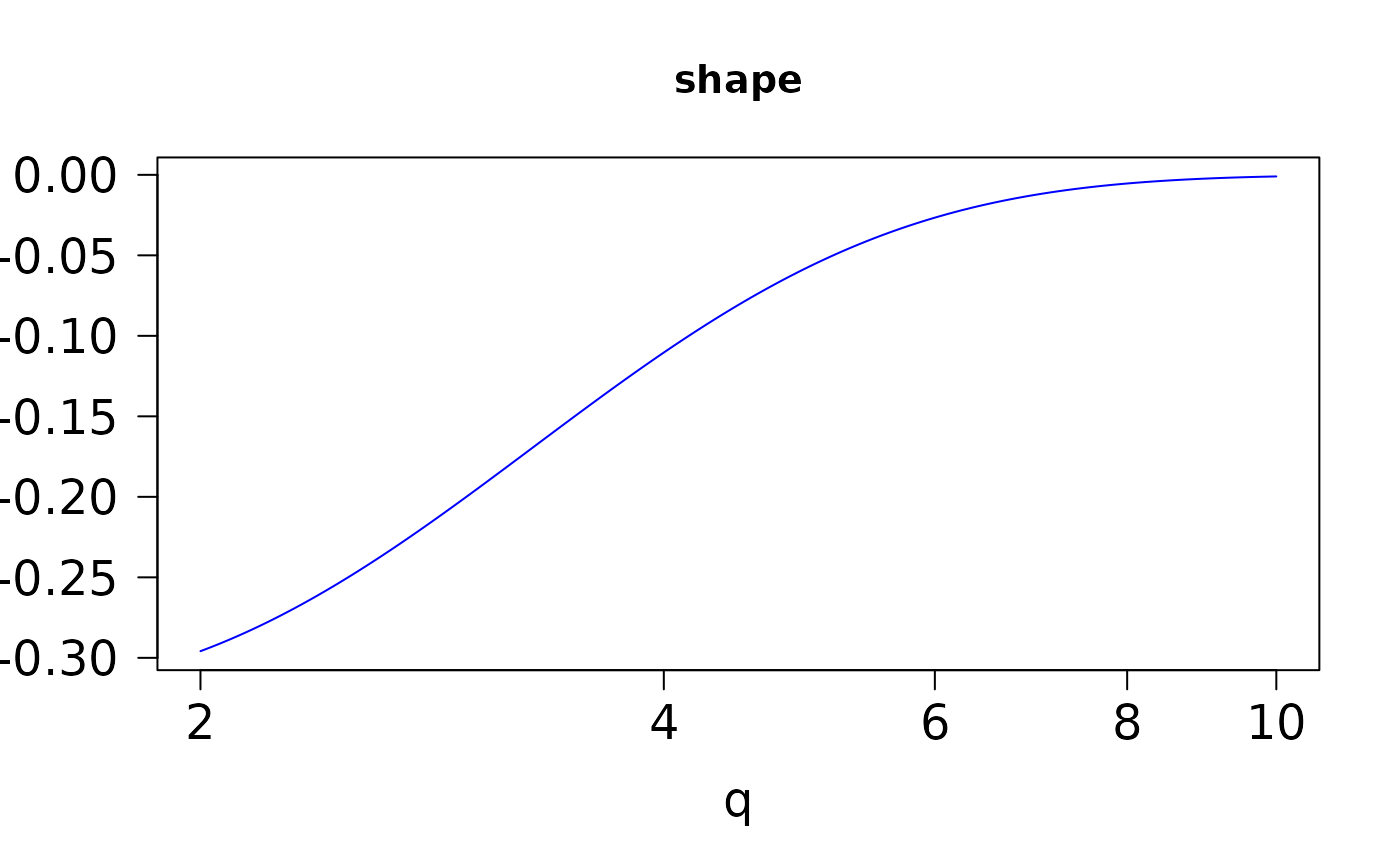
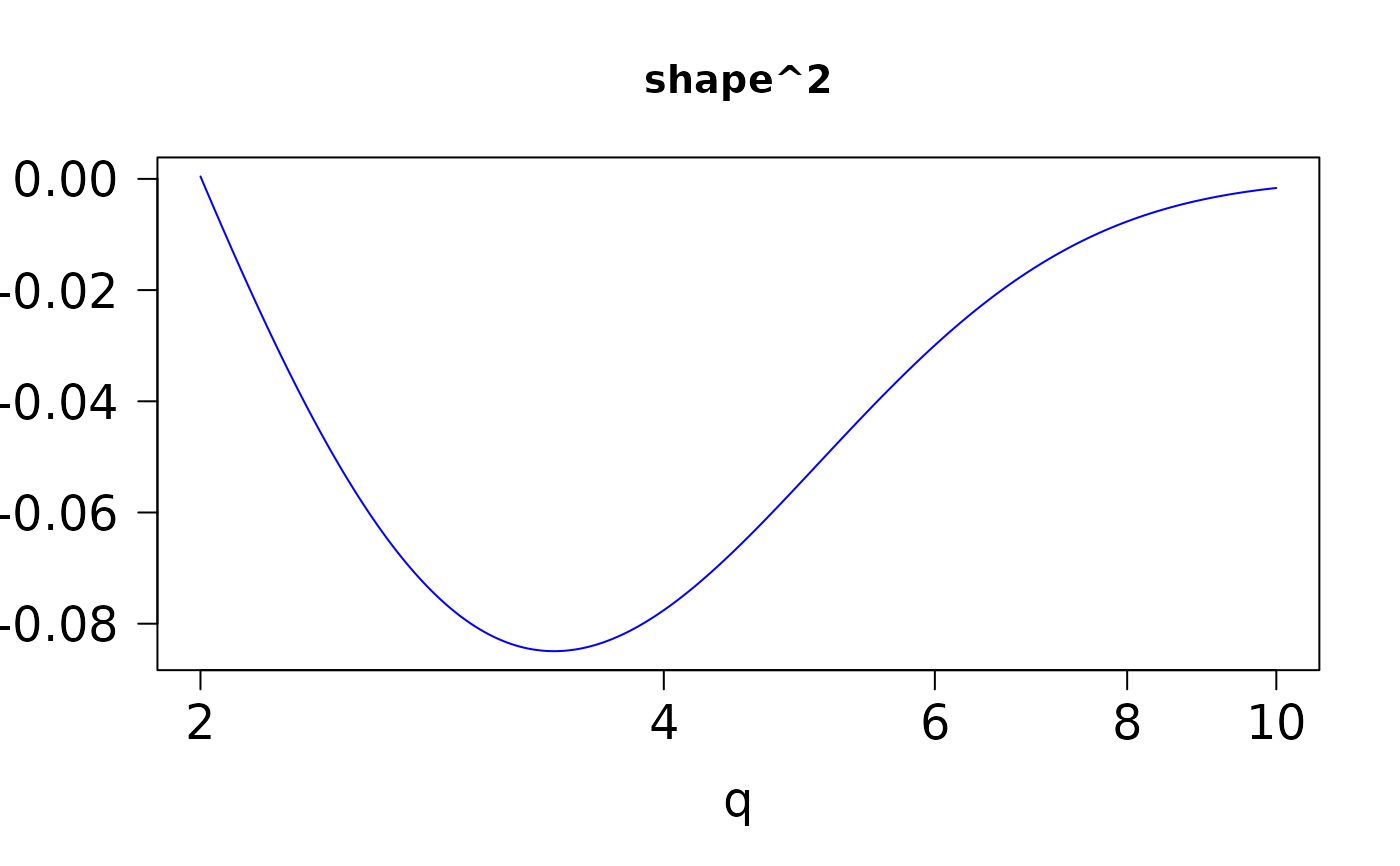
The first 5 columns, running from left to right, are the derivatives with respect to: $x$, $x^2$, $a$, $a^2$, $xa$. The 6th column is $P(a, x)$ (but it is not as accurate as calling pgamma directly).

References

Moore, R. J. (1982). Algorithm AS 187: Derivatives of the Incomplete Gamma Integral. Journal of the Royal Statistical Society, Series C (Applied Statistics), 31(3), 330–335.

Author

T. W. Yee wrote the wrapper function to the Fortran subroutine written by R. J. Moore. The subroutine was modified to run using double precision. The original code came from http://lib.stat.cmu.edu/apstat/187. but this website has since become stale.

Note

If convergence does not occur then try increasing the value of tmax.

Yet to do: add more arguments to give greater flexibility in the accuracy desired and to compute only quantities that are required by the user.

Examples

x <- seq(2, 10, length = 501)
head(ans <- pgamma.deriv(x, 2))
#>              q        q^2      shape       shape^2    q.shape pgamma(q, shape)
#> [1,] 0.2706706 -0.1353353 -0.2958549  0.0004420282 0.07317926        0.5939942
#> [2,] 0.2685053 -0.1353181 -0.2946052 -0.0018133884 0.07473335        0.5983076
#> [3,] 0.2663406 -0.1352675 -0.2933336 -0.0040379197 0.07623631        0.6025863
#> [4,] 0.2641769 -0.1351843 -0.2920409 -0.0062311686 0.07768898        0.6068305
#> [5,] 0.2620148 -0.1350697 -0.2907277 -0.0083927774 0.07909219        0.6110400
#> [6,] 0.2598548 -0.1349246 -0.2893947 -0.0105224259 0.08044679        0.6152149
if (FALSE)  par(mfrow = c(2, 3))
for (jay in 1:6)
  plot(x, ans[, jay], type = "l", col = "blue", cex.lab = 1.5,
       cex.axis = 1.5, las = 1, log = "x",
       main = colnames(ans)[jay], xlab = "q", ylab = "")  # \dontrun{}