Derivatives of the Incomplete Gamma Integral (Unscaled Version)

The first two derivatives of the incomplete gamma integral with scaling.

pgamma.deriv.unscaled(q, shape)

Arguments

q, shape: As in pgamma and pgamma.deriv but these must be vectors of positive values only and finite.

Details

Define $$G(x, a) = \int_0^x t^{a-1} e^{-t} dt$$ so that $G(x, a)$ is pgamma(x, a) * gamma(a). Write $x = q$ and shape = $a$. The 0th and first and second derivatives with respect to $a$ of $G$ are returned. This function is similar in spirit to pgamma.deriv but here there is no gamma function to scale things. Currently a 3-column matrix is returned (in the future this may change and an argument may be supplied so that only what is required by the user is computed.) This function is based on Wingo (1989).

Value

The 3 columns, running from left to right, are the 0:2th derivatives with respect to $a$.

References

See truncweibull.

Author

T. W. Yee.

Warning

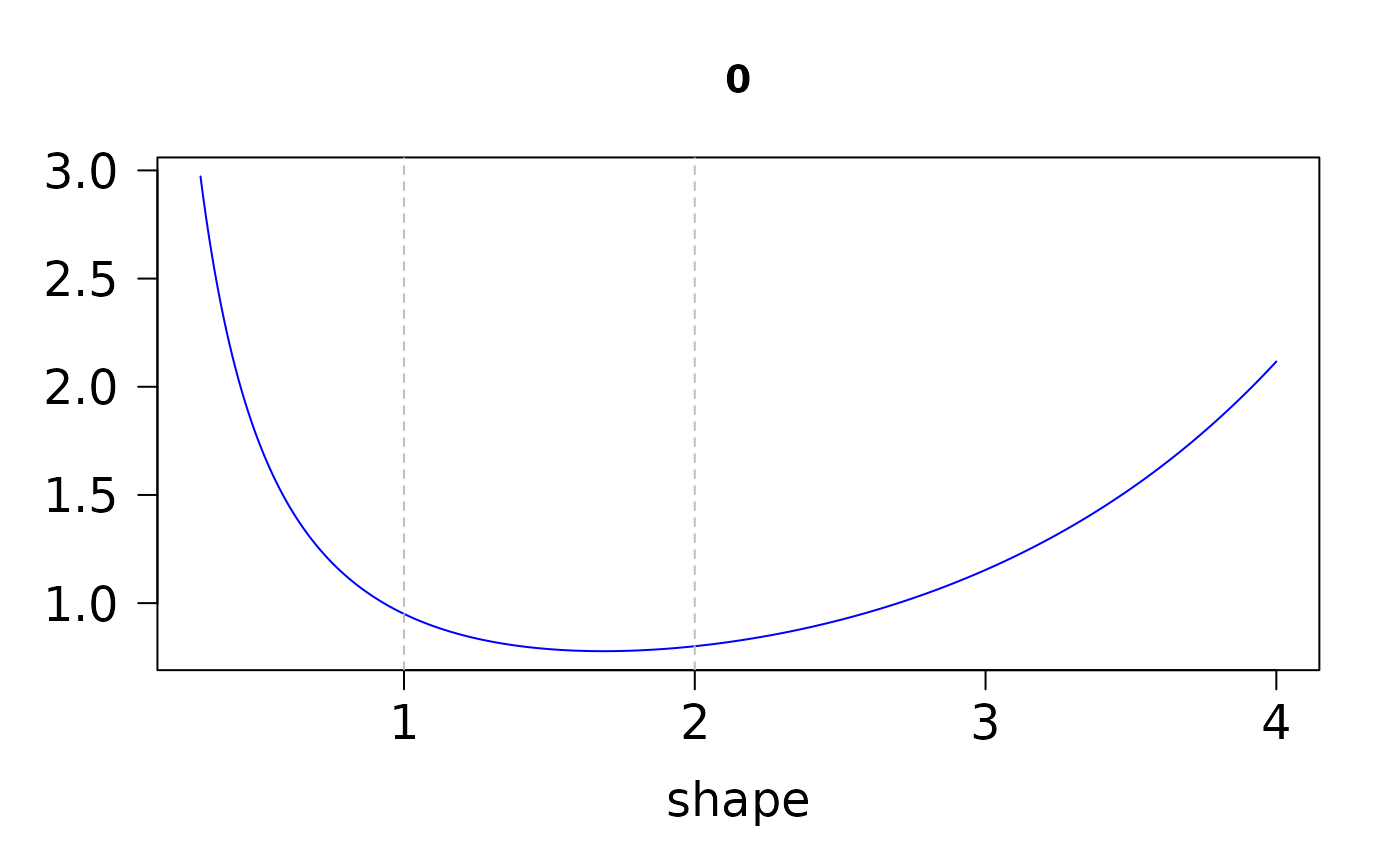
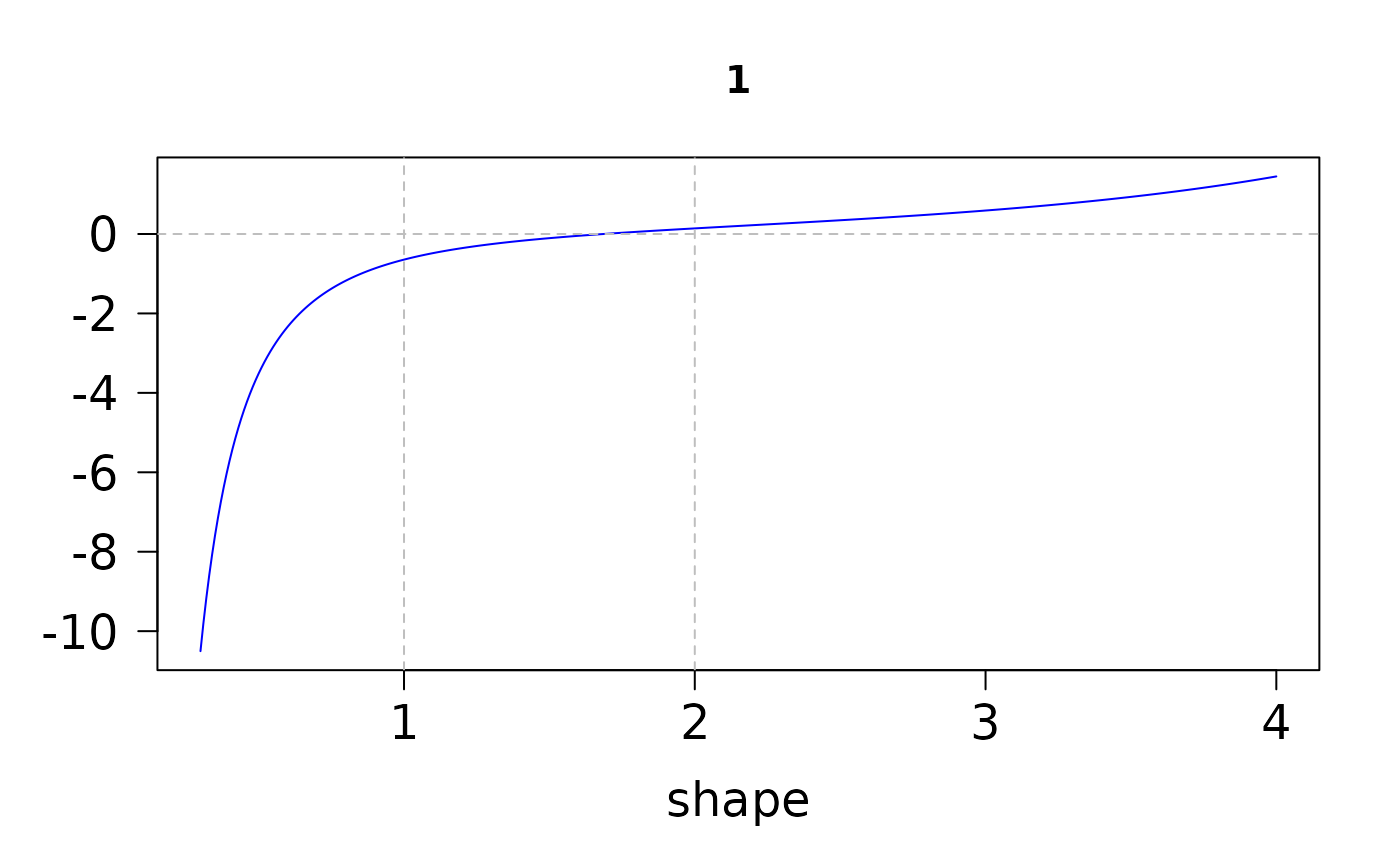
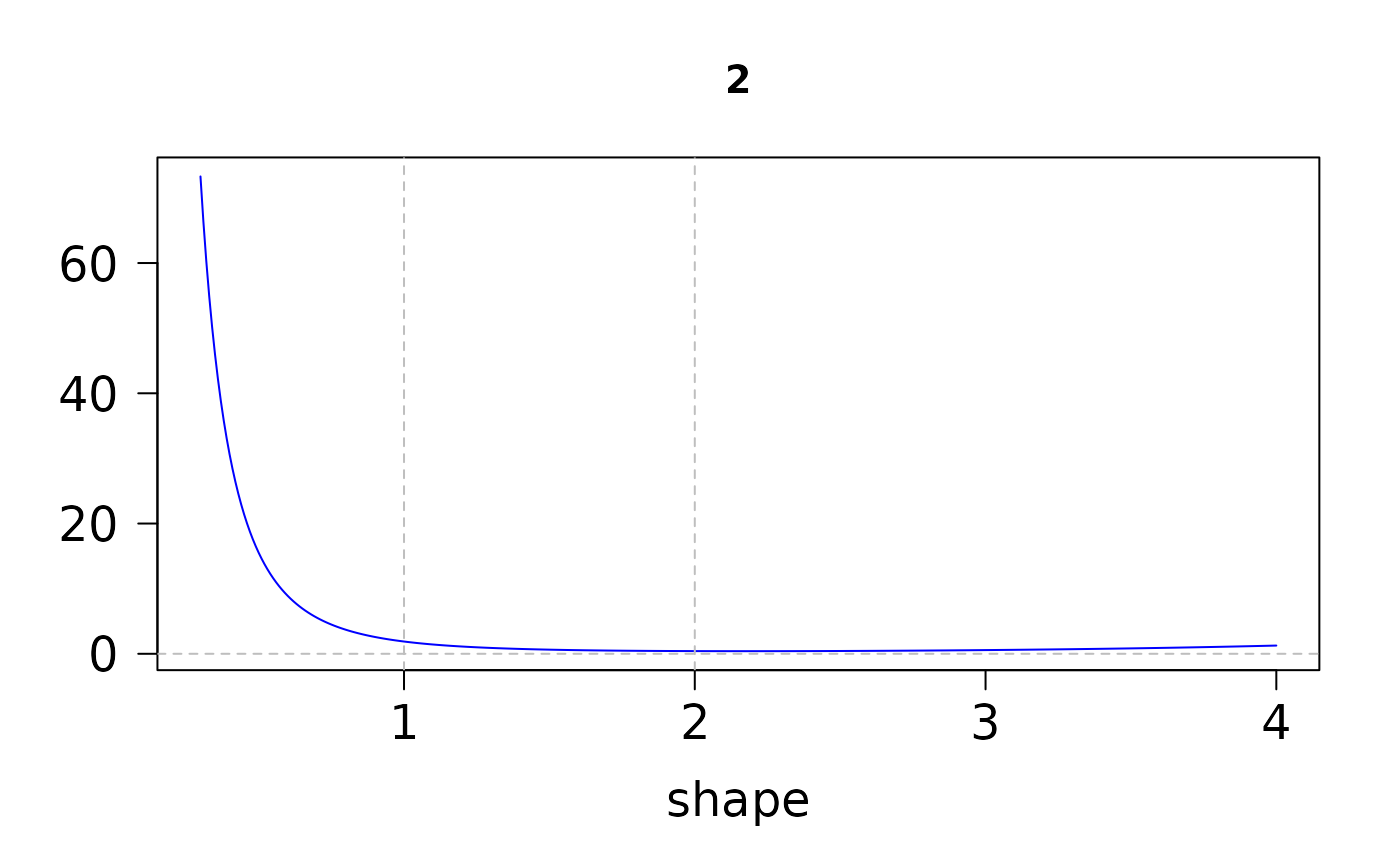
These function seems inaccurate for q = 1 and q = 2; see the plot below.

Examples

x <- 3; aa <- seq(0.3, 04, by = 0.01)
ans.u <- pgamma.deriv.unscaled(x, aa)
head(ans.u)
#>             0          1        2
#> [1,] 2.972153 -10.503878 73.29731
#> [2,] 2.870660  -9.806261 66.37775
#> [3,] 2.775811  -9.173526 60.29808
#> [4,] 2.686999  -8.597913 54.93484
#> [5,] 2.603685  -8.072785 50.18570
#> [6,] 2.525394  -7.592438 45.96540

if (FALSE)  par(mfrow = c(1, 3))
for (jay in 1:3) {
  plot(aa, ans.u[, jay], type = "l", col = "blue", cex.lab = 1.5,
       cex.axis = 1.5, las = 1, main = colnames(ans.u)[jay],
       log = "", xlab = "shape", ylab = "")
  abline(h = 0, v = 1:2, lty = "dashed", col = "gray")  # Inaccurate at 1 and 2
}



 # \dontrun{}