Zero-Inflated Geometric Distribution

Density, and random generation for the zero-inflated geometric distribution with parameter pstr0.

dzigeom(x, prob, pstr0 = 0, log = FALSE)
pzigeom(q, prob, pstr0 = 0)
qzigeom(p, prob, pstr0 = 0)
rzigeom(n, prob, pstr0 = 0)

Arguments

x, q

vector of quantiles.

p

vector of probabilities.

prob

see dgeom.

n

Same as in runif.

pstr0

Probability of structural zero (ignoring the geometric distribution), called \(\phi\). The default value corresponds to the response having an ordinary geometric distribution.

log

Logical. Return the logarithm of the answer?

Details

The probability function of \(Y\) is 0 with probability \(\phi\), and \(geometric(prob)\) with probability \(1-\phi\). Thus $$P(Y=0) =\phi + (1-\phi) P(W=0)$$ where \(W\) is distributed \(geometric(prob)\).

Value

dzigeom gives the density, pzigeom gives the distribution function, qzigeom gives the quantile function, and rzigeom generates random deviates.

Author

T. W. Yee

Note

The argument pstr0 is recycled to the required length, and must have values which lie in the interval \([0,1]\).

These functions actually allow for zero-deflation. That is, the resulting probability of a zero count is less than the nominal value of the parent distribution. See Zipois for more information.

See also

zigeometric, dgeom.

Examples

prob <- 0.5; pstr0 <- 0.2; x <- (-1):20
(ii <- dzigeom(x, prob, pstr0))
#>  [1] 0.000000e+00 6.000000e-01 2.000000e-01 1.000000e-01 5.000000e-02
#>  [6] 2.500000e-02 1.250000e-02 6.250000e-03 3.125000e-03 1.562500e-03
#> [11] 7.812500e-04 3.906250e-04 1.953125e-04 9.765625e-05 4.882813e-05
#> [16] 2.441406e-05 1.220703e-05 6.103516e-06 3.051758e-06 1.525879e-06
#> [21] 7.629395e-07 3.814697e-07
max(abs(cumsum(ii) - pzigeom(x, prob, pstr0)))  # Should be 0
#> [1] 2.220446e-16
table(rzigeom(1000, prob, pstr0))
#> 
#>   0   1   2   3   4   5   6   7   9 
#> 626 198  85  38  27  16   7   2   1 

if (FALSE)  x <- 0:10
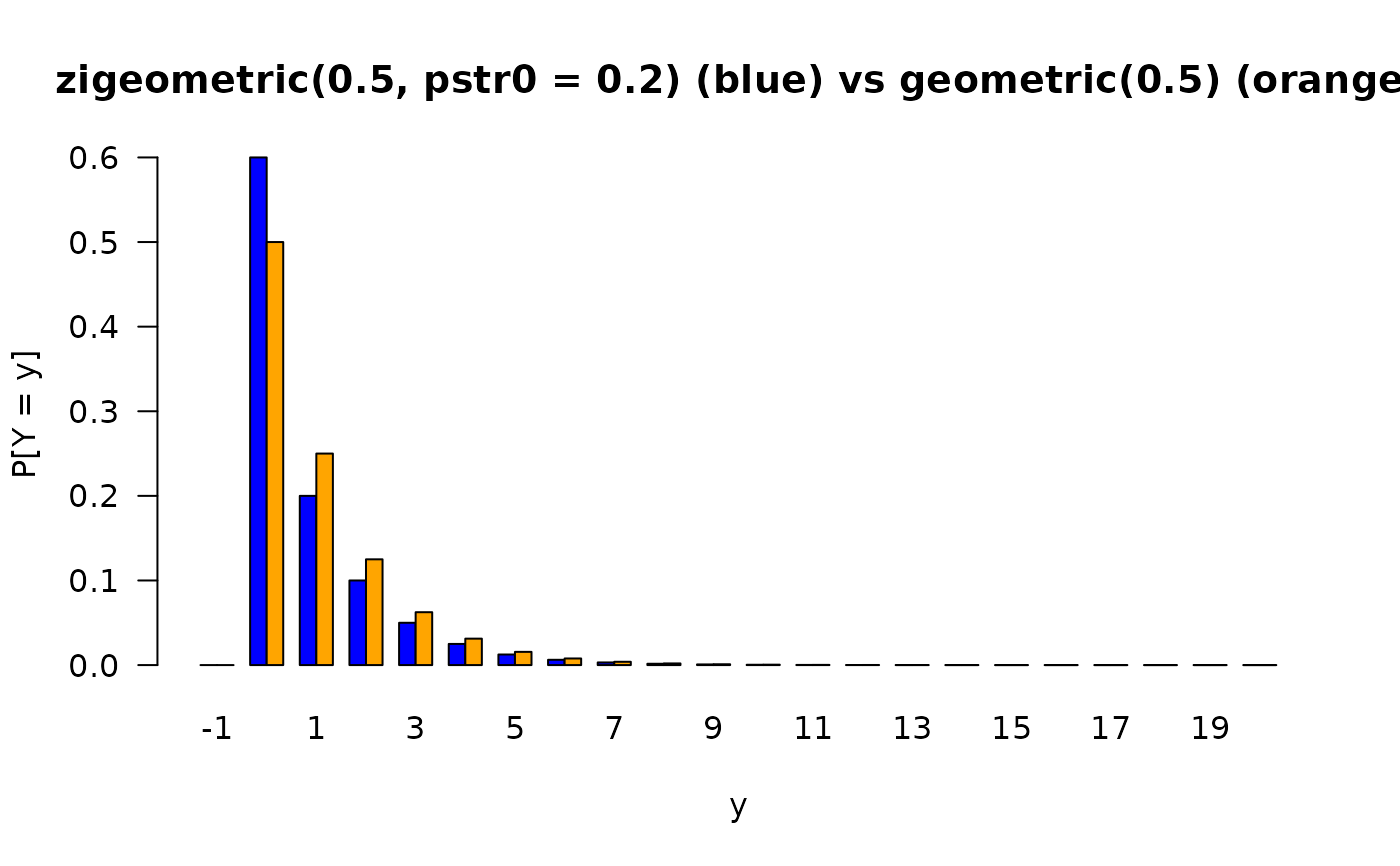
barplot(rbind(dzigeom(x, prob, pstr0), dgeom(x, prob)),
   beside = TRUE, col = c("blue","orange"),
   ylab = "P[Y = y]", xlab = "y", las = 1,
   main = paste0("zigeometric(", prob, ", pstr0 = ", pstr0,
                 ") (blue) vs", " geometric(", prob, ") (orange)"),
   names.arg = as.character(x))  # \dontrun{}