Reorder a correlation matrix.

Source: R/corrMatOrder.R

Draw rectangle(s) around the chart of corrrlation matrix based on the number of each cluster's members.

corrMatOrder(
  corr,
  order = c("AOE", "FPC", "hclust", "alphabet"),
  hclust.method = c("complete", "ward", "ward.D", "ward.D2", "single", "average",
    "mcquitty", "median", "centroid")
)

Arguments

corr

Correlation matrix to reorder.

order

Character, the ordering method for the correlation matrix.

  • 'AOE' for the angular order of the eigenvectors. It is calculated from the order of the angles, \(a_i\): $$ a_i = arctan (e_{i2} / e_{i1}), if e_{i1} > 0$$ $$ a_i = arctan (e_{i2} / e_{i1}) + \pi, otherwise.$$ where \(e_1\) and \(e_2\) are the largest two eigenvalues of matrix corr. See Michael Friendly (2002) for details.

  • 'FPC' for the first principal component order.

  • 'hclust' for hierarchical clustering order.

  • 'alphabet' for alphabetical order.

hclust.method

Character, the agglomeration method to be used when order is hclust. This should be one of 'ward', 'ward.D', 'ward.D2', 'single', 'complete', 'average', 'mcquitty', 'median' or 'centroid'.

Value

Returns a single permutation vector.

See also

Package seriation offers more methods to reorder matrices, such as ARSA, BBURCG, BBWRCG, MDS, TSP, Chen and so forth.

Author

Taiyun Wei

Examples

M = cor(mtcars)

(order.AOE = corrMatOrder(M, order = 'AOE'))
#>  [1] 10  9  5  1  8  7  6  3  2  4 11
(order.FPC = corrMatOrder(M, order = 'FPC'))
#>  [1]  2  3  6  4 11  7 10  9  5  8  1
(order.hc = corrMatOrder(M, order = 'hclust'))
#>  [1] 11  6  4  2  3  7  8  1  5  9 10
(order.hc2 = corrMatOrder(M, order = 'hclust', hclust.method = 'ward.D'))
#>  [1]  6  2  3  4 11  7  8  9 10  1  5

M.AOE = M[order.AOE, order.AOE]
M.FPC = M[order.FPC, order.FPC]
M.hc  = M[order.hc, order.hc]
M.hc2 = M[order.hc2, order.hc2]



par(ask = TRUE)
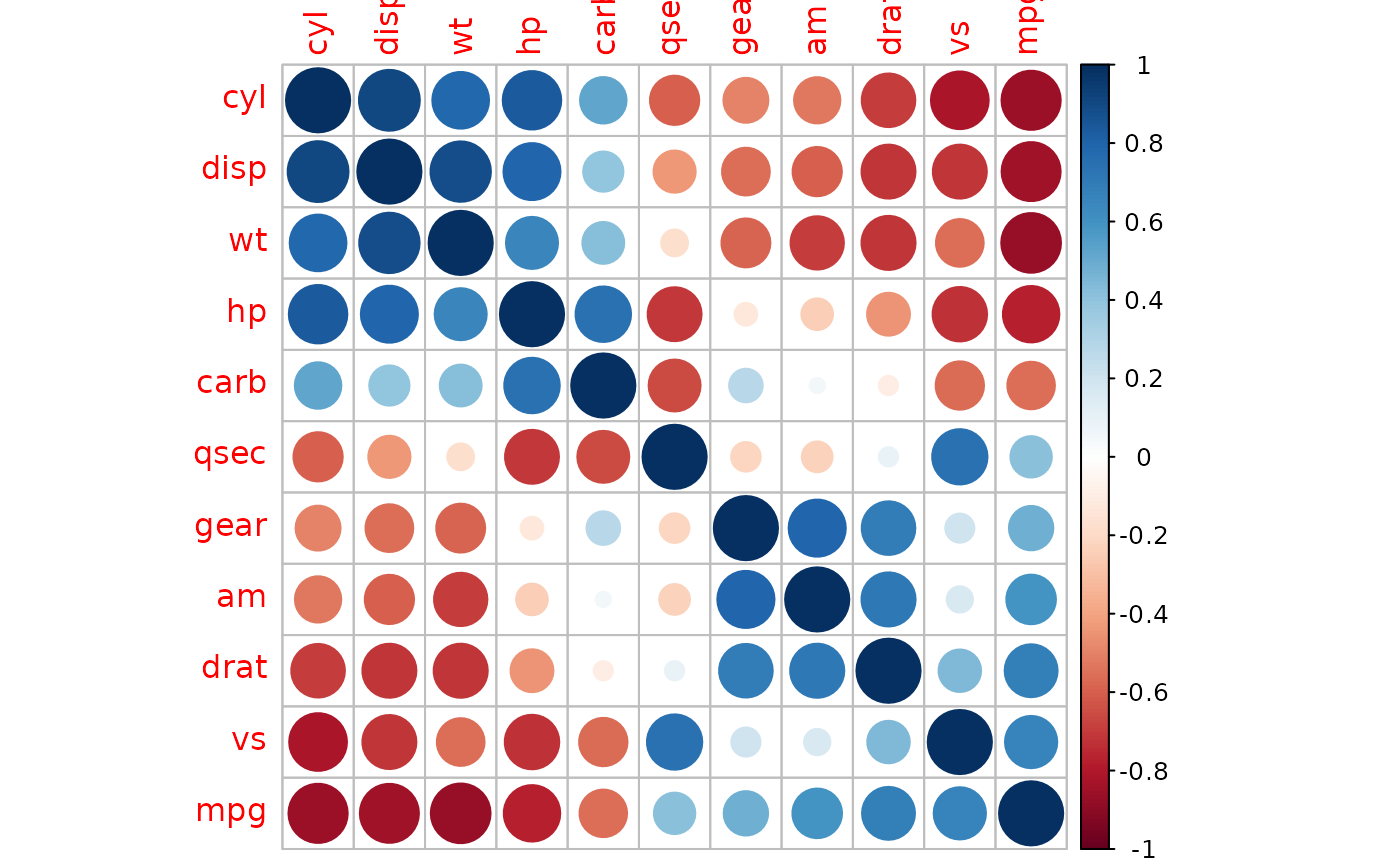
corrplot(M)

corrplot(M.AOE)

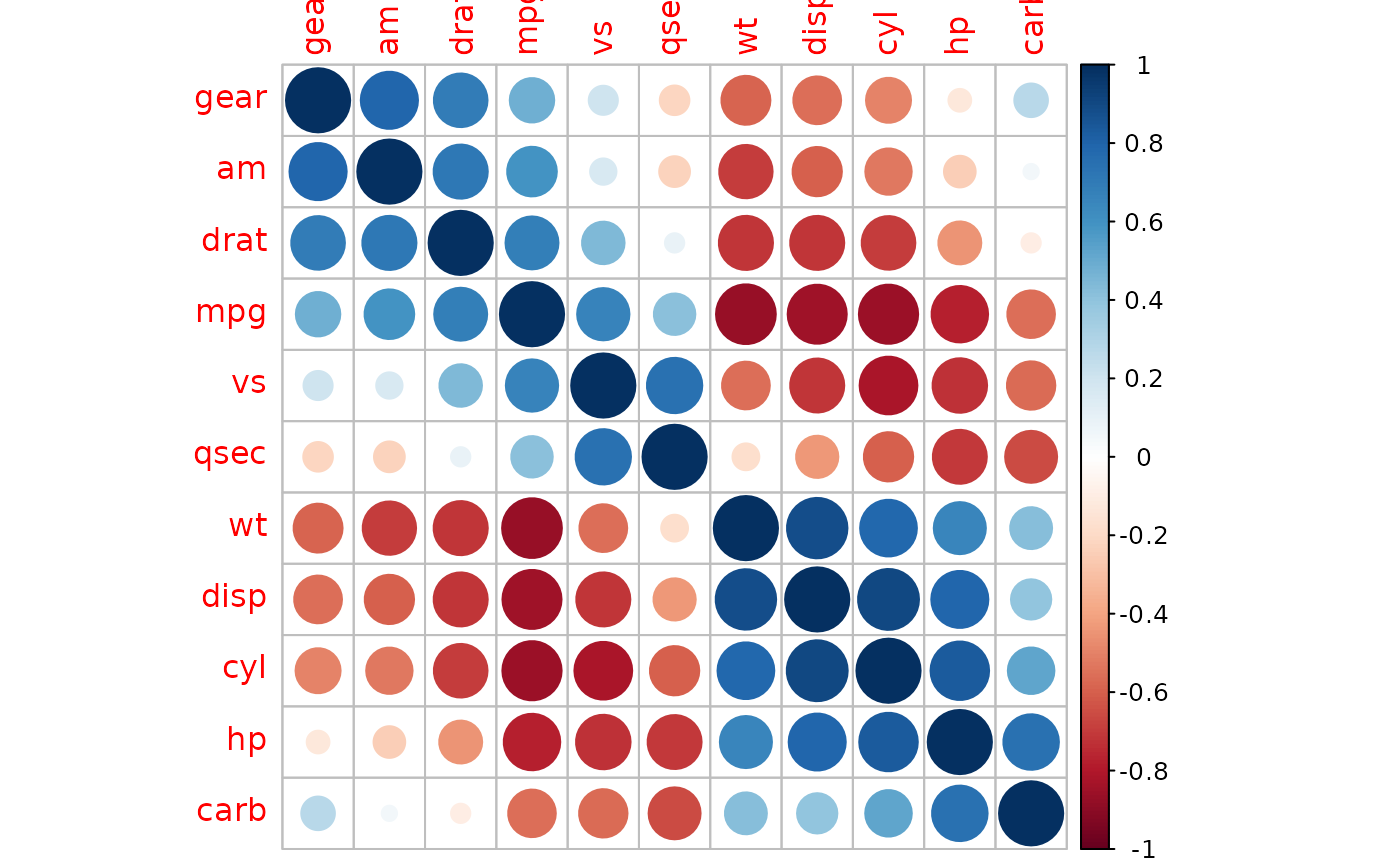corrplot(M.FPC)

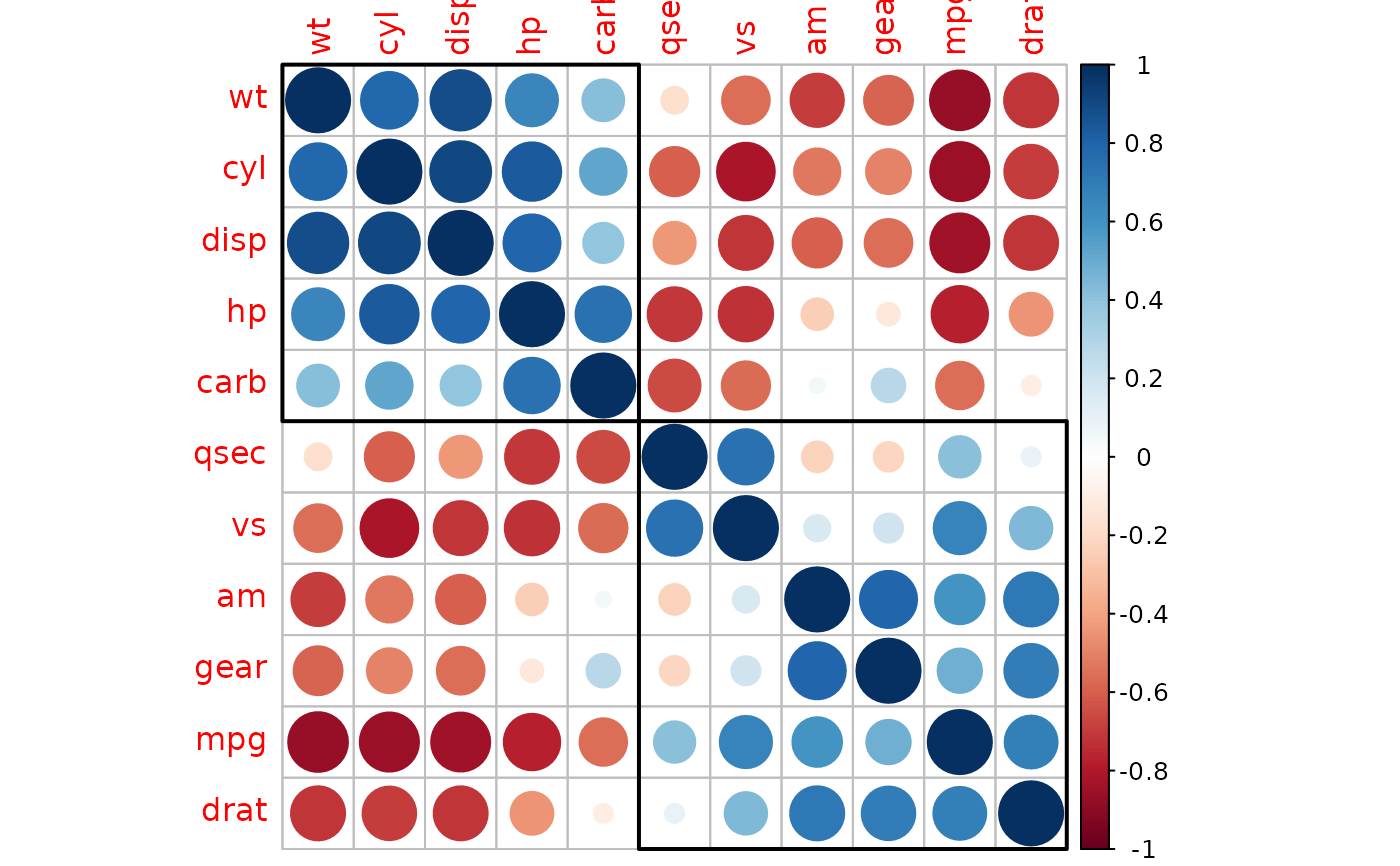
corrplot(M.hc)

corrplot(M.hc)
corrRect.hclust(corr = M.hc, k = 2)


corrplot(M.hc)
corrRect.hclust(corr = M.hc, k = 3)


corrplot(M.hc2)
corrRect.hclust(M.hc2, k = 2, method = 'ward.D')