Yield of dyestuff by batch

The Dyestuff data frame provides the yield of dyestuff (Naphthalene Black 12B) from 5 different preparations from each of 6 different batchs of an intermediate product (H-acid). The Dyestuff2 data were generated data in the same structure but with a large residual variance relative to the batch variance.

Format

Data frames, each with 30 observations on the following 2 variables.

Batch

a factor indicating the batch of the intermediate product from which the preparation was created.

Yield

the yield of dyestuff from the preparation (grams of standard color).

Source

O.L. Davies and P.L. Goldsmith (eds), Statistical Methods in Research and Production, 4th ed., Oliver and Boyd, (1972), section 6.4

G.E.P. Box and G.C. Tiao, Bayesian Inference in Statistical Analysis, Addison-Wesley, (1973), section 5.1.2

Details

The Dyestuff data are described in Davies and Goldsmith (1972) as coming from “an investigation to find out how much the variation from batch to batch in the quality of an intermediate product (H-acid) contributes to the variation in the yield of the dyestuff (Naphthalene Black 12B) made from it. In the experiment six samples of the intermediate, representing different batches of works manufacture, were obtained, and five preparations of the dyestuff were made in the laboratory from each sample. The equivalent yield of each preparation as grams of standard colour was determined by dye-trial.”

The Dyestuff2 data are described in Box and Tiao (1973) as illustrating “ the case where between-batches mean square is less than the within-batches mean square. These data had to be constructed for although examples of this sort undoubtably occur in practice, they seem to be rarely published.”

Examples

#> R_LIBS:
#> and extra(:= not in R_LIBS) .libPaths():
#> Matrix -- built: R 4.4.1; x86_64-pc-linux-gnu; 2024-08-22 01:54:16 UTC; unix
#>        -- dir  : /opt/R/4.4.1/lib/R/library/Matrix
#> Rcpp -- built: R 4.4.1; x86_64-pc-linux-gnu; 2025-01-26 16:15:49 UTC; unix
#>      -- dir  : /cluster-data/user-homes/elizabethb/projects/prism-pkgdocs-build/installed-pkgs/lme4_1.1-36_lib/Rcpp
#> RcppEigen -- built: R 4.4.1; x86_64-pc-linux-gnu; 2025-01-26 16:17:44 UTC; unix
#>           -- dir  : /cluster-data/user-homes/elizabethb/projects/prism-pkgdocs-build/installed-pkgs/lme4_1.1-36_lib/RcppEigen
#> minqa -- built: R 4.4.1; x86_64-pc-linux-gnu; 2025-01-26 16:17:40 UTC; unix
#>       -- dir  : /cluster-data/user-homes/elizabethb/projects/prism-pkgdocs-build/installed-pkgs/lme4_1.1-36_lib/minqa
#> lme4 -- built: R 4.4.1; x86_64-pc-linux-gnu; 2025-05-13 19:28:27 UTC; unix
#>      -- dir  : /tmp/Rtmp4s2u6A/temp_libpath3b9f81ce8fad4/lme4
require(lattice)
str(Dyestuff)
#> 'data.frame':	30 obs. of  2 variables:
#>  $ Batch: Factor w/ 6 levels "A","B","C","D",..: 1 1 1 1 1 2 2 2 2 2 ...
#>  $ Yield: num  1545 1440 1440 1520 1580 ...
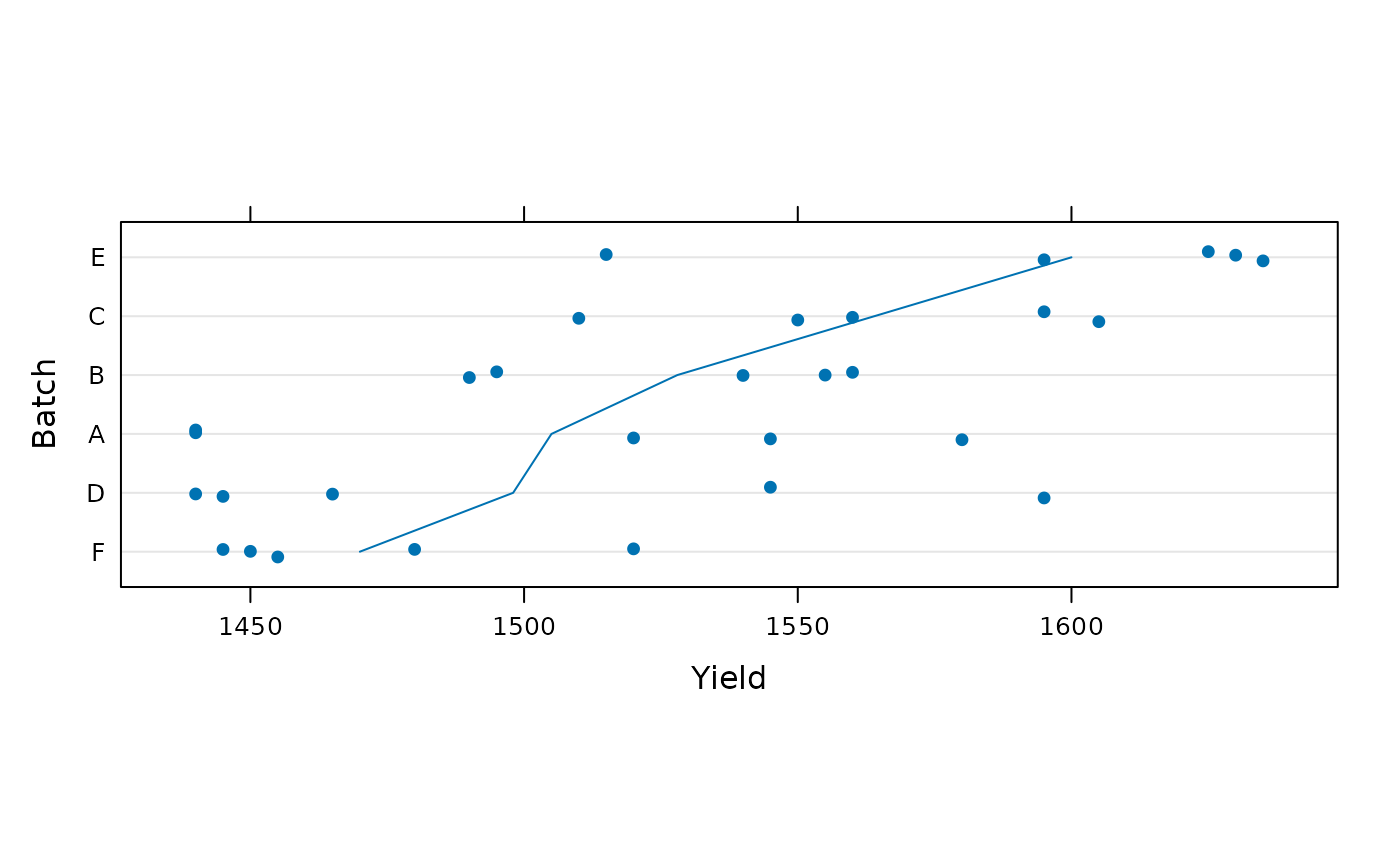
dotplot(reorder(Batch, Yield) ~ Yield, Dyestuff,
        ylab = "Batch", jitter.y = TRUE, aspect = 0.3,
        type = c("p", "a"))

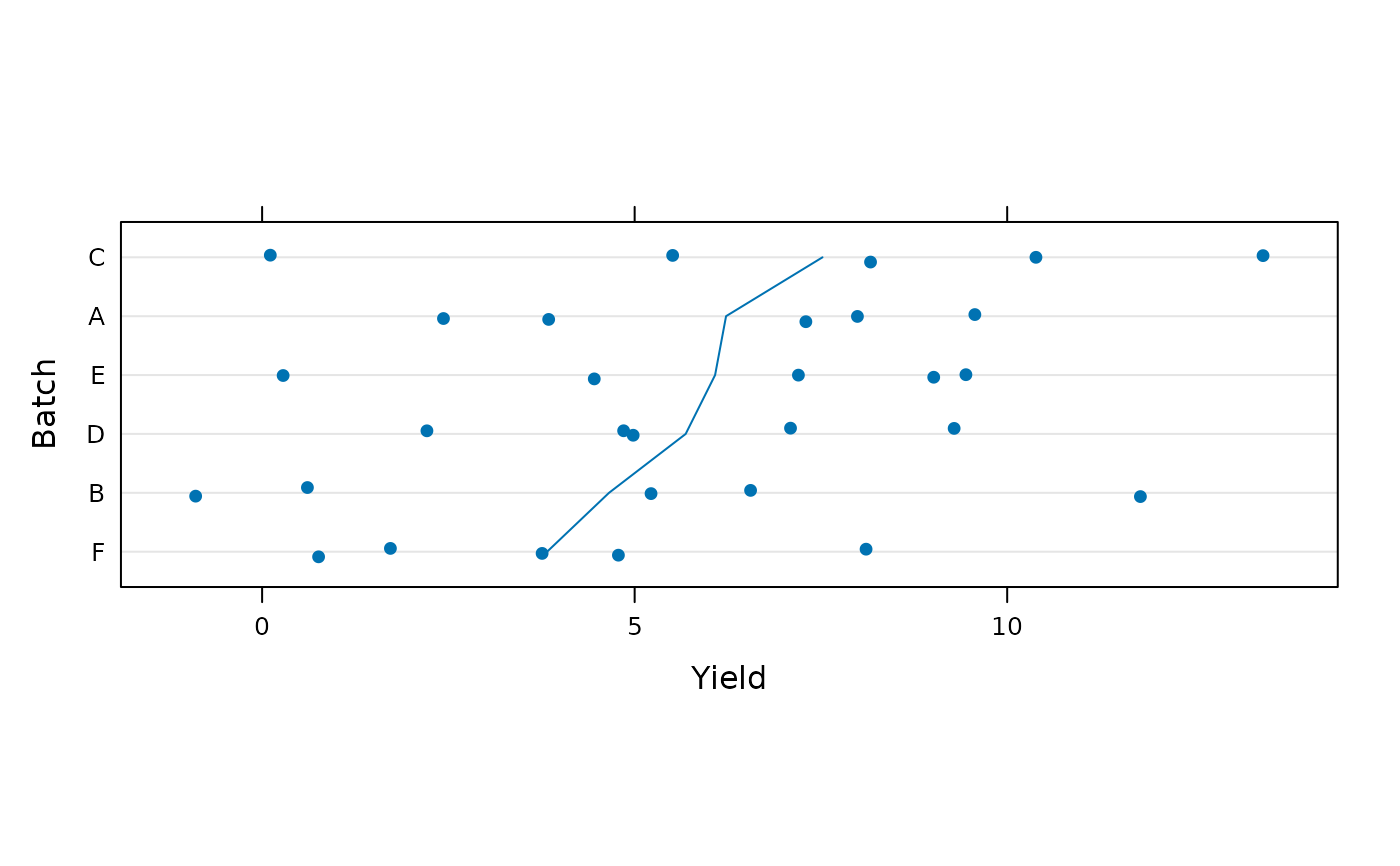
dotplot(reorder(Batch, Yield) ~ Yield, Dyestuff2,
        ylab = "Batch", jitter.y = TRUE, aspect = 0.3,
        type = c("p", "a"))

(fm1 <- lmer(Yield ~ 1|Batch, Dyestuff))
#> Linear mixed model fit by REML ['lmerMod']
#> Formula: Yield ~ 1 | Batch
#>    Data: Dyestuff
#> REML criterion at convergence: 319.6543
#> Random effects:
#>  Groups   Name        Std.Dev.
#>  Batch    (Intercept) 42.00   
#>  Residual             49.51   
#> Number of obs: 30, groups:  Batch, 6
#> Fixed Effects:
#> (Intercept)  
#>        1528  
(fm2 <- lmer(Yield ~ 1|Batch, Dyestuff2))
#> boundary (singular) fit: see help('isSingular')
#> Linear mixed model fit by REML ['lmerMod']
#> Formula: Yield ~ 1 | Batch
#>    Data: Dyestuff2
#> REML criterion at convergence: 161.8283
#> Random effects:
#>  Groups   Name        Std.Dev.
#>  Batch    (Intercept) 0.000   
#>  Residual             3.716   
#> Number of obs: 30, groups:  Batch, 6
#> Fixed Effects:
#> (Intercept)  
#>       5.666  
#> optimizer (nloptwrap) convergence code: 0 (OK) ; 0 optimizer warnings; 1 lme4 warnings