Standard 'nls' framework that uses 'nls.lm' for fitting
nlsLM.RdnlsLM is a modified version of nls that uses nls.lm for fitting.
Since an object of class 'nls' is returned, all generic functions such as anova,
coef, confint, deviance, df.residual,
fitted, formula, logLik, predict,
print, profile, residuals, summary,
update, vcov and weights are applicable.
nlsLM(formula, data = parent.frame(), start, jac = NULL,
algorithm = "LM", control = nls.lm.control(),
lower = NULL, upper = NULL, trace = FALSE, subset,
weights, na.action, model = FALSE, ...)Arguments
- formula
a nonlinear model
formulaincluding variables and parameters. Will be coerced to a formula if necessary.- data
an optional data frame in which to evaluate the variables in
formulaandweights. Can also be a list or an environment, but not a matrix.- start
a named list or named numeric vector of starting estimates.
- jac
A function to return the Jacobian.
- algorithm
only method
"LM"(Levenberg-Marquardt) is implemented.- control
an optional list of control settings. See
nls.lm.controlfor the names of the settable control values and their effect.- lower
A numeric vector of lower bounds on each parameter. If not given, the default lower bound for each parameter is set to
-Inf.- upper
A numeric vector of upper bounds on each parameter. If not given, the default upper bound for each parameter is set to
Inf.- trace
logical value indicating if a trace of the iteration progress should be printed. Default is
FALSE. IfTRUE, the residual (weighted) sum-of-squares and the parameter values are printed at the conclusion of each iteration.- subset
an optional vector specifying a subset of observations to be used in the fitting process.
- weights
an optional numeric vector of (fixed) weights. When present, the objective function is weighted least squares. See the
wfctfunction for options for easy specification of weighting schemes.- na.action
a function which indicates what should happen when the data contain
NAs. The default is set by thena.actionsetting ofoptions, and isna.failif that is unset. The ‘factory-fresh’ default isna.omit. Valuena.excludecan be useful.- model
logical. If true, the model frame is returned as part of the object. Default is
FALSE.- ...
Additional optional arguments. None are used at present.
Details
The standard nls function was modified in several ways to incorporate the Levenberg-Marquardt type nls.lm fitting algorithm. The formula is transformed into a function that returns a vector of (weighted) residuals whose sum square is minimized by nls.lm. The optimized parameters are then transferred
to nlsModel in order to obtain an object of class 'nlsModel'. The internal C function C_nls_iter and nls_port_fit were removed to avoid subsequent "Gauss-Newton", "port" or "plinear" types of optimization of nlsModel. Several other small modifications were made in order to make all generic functions work on the output.
Value
A list of
- m
an
nlsModelobject incorporating the model.- data
the expression that was passed to
nlsas the data argument. The actual data values are present in the environment of themcomponent.- call
the matched call.
- convInfo
a list with convergence information.
- control
the control
listused, see thecontrolargument.- na.action
the
"na.action"attribute (if any) of the model frame.- dataClasses
the
"dataClasses"attribute (if any) of the"terms"attribute of the model frame.- model
if
model = TRUE, the model frame.- weights
if
weightsis supplied, the weights.
References
Bates, D. M. and Watts, D. G. (1988) Nonlinear Regression Analysis and Its Applications, Wiley
Bates, D. M. and Chambers, J. M. (1992) Nonlinear models. Chapter 10 of Statistical Models in S eds J. M. Chambers and T. J. Hastie, Wadsworth & Brooks/Cole.
J.J. More, "The Levenberg-Marquardt algorithm: implementation and theory," in Lecture Notes in Mathematics 630: Numerical Analysis, G.A. Watson (Ed.), Springer-Verlag: Berlin, 1978, pp. 105-116.
See also
Examples
### Examples from 'nls' doc ###
DNase1 <- subset(DNase, Run == 1)
## using a selfStart model
fm1DNase1 <- nlsLM(density ~ SSlogis(log(conc), Asym, xmid, scal), DNase1)
## using logistic formula
fm2DNase1 <- nlsLM(density ~ Asym/(1 + exp((xmid - log(conc))/scal)),
data = DNase1,
start = list(Asym = 3, xmid = 0, scal = 1))
## all generics are applicable
coef(fm1DNase1)
#> Asym xmid scal
#> 2.345179 1.483089 1.041455
confint(fm1DNase1)
#> Waiting for profiling to be done...
#> 2.5% 97.5%
#> Asym 2.1935438 2.538804
#> xmid 1.3214540 1.678751
#> scal 0.9743072 1.114939
deviance(fm1DNase1)
#> [1] 0.004789569
df.residual(fm1DNase1)
#> [1] 13
fitted(fm1DNase1)
#> [1] 0.03068064 0.03068064 0.11205118 0.11205118 0.20858036 0.20858036
#> [7] 0.37432769 0.37432769 0.63277780 0.63277780 0.98086295 0.98086295
#> [13] 1.36751306 1.36751306 1.71498779 1.71498779
#> attr(,"label")
#> [1] "Fitted values"
formula(fm1DNase1)
#> density ~ SSlogis(log(conc), Asym, xmid, scal)
#> <environment: 0x55d2ab0953a8>
logLik(fm1DNase1)
#> 'log Lik.' 42.20821 (df=4)
predict(fm1DNase1)
#> [1] 0.03068064 0.03068064 0.11205118 0.11205118 0.20858036 0.20858036
#> [7] 0.37432769 0.37432769 0.63277780 0.63277780 0.98086295 0.98086295
#> [13] 1.36751306 1.36751306 1.71498779 1.71498779
print(fm1DNase1)
#> Nonlinear regression model
#> model: density ~ SSlogis(log(conc), Asym, xmid, scal)
#> data: DNase1
#> Asym xmid scal
#> 2.345 1.483 1.041
#> residual sum-of-squares: 0.00479
#>
#> Number of iterations to convergence: 1
#> Achieved convergence tolerance: 1.49e-08
profile(fm1DNase1)
#> $Asym
#> tau par.vals.Asym par.vals.xmid par.vals.scal
#> 1 -3.1914606 2.1319546 1.2580938 0.9550832
#> 2 -2.5507631 2.1694848 1.2985073 0.9713316
#> 3 -1.9083874 2.2095019 1.3412362 0.9881539
#> 4 -1.2642540 2.2522874 1.3864854 1.0055751
#> 5 -0.6192425 2.2980951 1.4344101 1.0235946
#> 6 0.0000000 2.3451793 1.4830894 1.0414547
#> 7 0.5789576 2.3922635 1.5311646 1.0586671
#> 8 1.1425581 2.4412587 1.5805380 1.0759170
#> 9 1.7052559 2.4936315 1.6325701 1.0936421
#> 10 2.2665307 2.5497048 1.6874200 1.1118405
#> 11 2.8263175 2.6098922 1.7453054 1.1305244
#> 12 3.3845279 2.6746671 1.8064645 1.1497058
#>
#> $xmid
#> tau par.vals.Asym par.vals.xmid par.vals.scal
#> 1 -3.1513227 2.1381905 1.2561672 0.9566499
#> 2 -2.5186865 2.1744539 1.2972549 0.9724156
#> 3 -1.8849168 2.2131885 1.3404782 0.9888309
#> 4 -1.2500053 2.2546517 1.3860301 1.0059119
#> 5 -0.6145420 2.2990954 1.4340777 1.0236589
#> 6 0.0000000 2.3451793 1.4830894 1.0414547
#> 7 0.5829776 2.3920229 1.5321010 1.0589249
#> 8 1.1546718 2.4412376 1.5827501 1.0766261
#> 9 1.7257877 2.4939999 1.6361245 1.0948857
#> 10 2.2960387 2.5506767 1.6924277 1.1137065
#> 11 2.8654051 2.6117173 1.7519106 1.1331007
#> 12 3.4338551 2.6776418 1.8148503 1.1530812
#>
#> $scal
#> tau par.vals.Asym par.vals.xmid par.vals.scal
#> 1 -3.0759196 2.1593480 1.2849790 0.9475341
#> 2 -2.4588908 2.1920488 1.3202832 0.9654720
#> 3 -1.8415854 2.2268464 1.3576694 0.9838520
#> 4 -1.2239983 2.2639478 1.3972957 1.0026937
#> 5 -0.6062726 2.3035781 1.4393264 1.0220130
#> 6 0.0000000 2.3451793 1.4830894 1.0414547
#> 7 0.5913415 2.3886105 1.5283601 1.0608964
#> 8 1.1789260 2.4348607 1.5760767 1.0807035
#> 9 1.7662969 2.4845150 1.6267168 1.1010119
#> 10 2.3534044 2.5379559 1.6805174 1.1218418
#> 11 2.9402428 2.5956309 1.7377473 1.1432162
#> 12 3.5268050 2.6580542 1.7987014 1.1651594
#>
#> attr(,"original.fit")
#> Nonlinear regression model
#> model: density ~ SSlogis(log(conc), Asym, xmid, scal)
#> data: DNase1
#> Asym xmid scal
#> 2.345 1.483 1.041
#> residual sum-of-squares: 0.00479
#>
#> Number of iterations to convergence: 1
#> Achieved convergence tolerance: 1.49e-08
#> attr(,"summary")
#>
#> Formula: density ~ SSlogis(log(conc), Asym, xmid, scal)
#>
#> Parameters:
#> Estimate Std. Error t value Pr(>|t|)
#> Asym 2.34518 0.07815 30.01 2.17e-13 ***
#> xmid 1.48309 0.08135 18.23 1.22e-10 ***
#> scal 1.04145 0.03227 32.27 8.51e-14 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> Residual standard error: 0.01919 on 13 degrees of freedom
#>
#> Number of iterations to convergence: 1
#> Achieved convergence tolerance: 1.49e-08
#>
#> attr(,"class")
#> [1] "profile.nls" "profile"
residuals(fm1DNase1)
#> [1] -0.0136806435 -0.0126806435 0.0089488190 0.0119488190 -0.0025803626
#> [6] 0.0064196374 0.0026723138 -0.0003276862 -0.0187778006 -0.0237778006
#> [11] 0.0381370470 0.0201370470 -0.0335130604 -0.0035130604 0.0150122115
#> [16] -0.0049877885
#> attr(,"label")
#> [1] "Residuals"
summary(fm1DNase1)
#>
#> Formula: density ~ SSlogis(log(conc), Asym, xmid, scal)
#>
#> Parameters:
#> Estimate Std. Error t value Pr(>|t|)
#> Asym 2.34518 0.07815 30.01 2.17e-13 ***
#> xmid 1.48309 0.08135 18.23 1.22e-10 ***
#> scal 1.04145 0.03227 32.27 8.51e-14 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> Residual standard error: 0.01919 on 13 degrees of freedom
#>
#> Number of iterations to convergence: 1
#> Achieved convergence tolerance: 1.49e-08
#>
update(fm1DNase1)
#> Nonlinear regression model
#> model: density ~ SSlogis(log(conc), Asym, xmid, scal)
#> data: DNase1
#> Asym xmid scal
#> 2.345 1.483 1.041
#> residual sum-of-squares: 0.00479
#>
#> Number of iterations to convergence: 1
#> Achieved convergence tolerance: 1.49e-08
vcov(fm1DNase1)
#> Asym xmid scal
#> Asym 0.006108024 0.006273982 0.002271987
#> xmid 0.006273982 0.006618332 0.002379384
#> scal 0.002271987 0.002379384 0.001041404
weights(fm1DNase1)
#> NULL
## weighted nonlinear regression using
## inverse squared variance of the response
## gives same results as original 'nls' function
Treated <- Puromycin[Puromycin$state == "treated", ]
var.Treated <- tapply(Treated$rate, Treated$conc, var)
var.Treated <- rep(var.Treated, each = 2)
Pur.wt1 <- nls(rate ~ (Vm * conc)/(K + conc), data = Treated,
start = list(Vm = 200, K = 0.1), weights = 1/var.Treated^2)
Pur.wt2 <- nlsLM(rate ~ (Vm * conc)/(K + conc), data = Treated,
start = list(Vm = 200, K = 0.1), weights = 1/var.Treated^2)
all.equal(coef(Pur.wt1), coef(Pur.wt2))
#> [1] TRUE
## 'nlsLM' can fit zero-noise data
## in contrast to 'nls'
x <- 1:10
y <- 2*x + 3
if (FALSE) { # \dontrun{
nls(y ~ a + b * x, start = list(a = 0.12345, b = 0.54321))
} # }
nlsLM(y ~ a + b * x, start = list(a = 0.12345, b = 0.54321))
#> Nonlinear regression model
#> model: y ~ a + b * x
#> data: parent.frame()
#> a b
#> 3 2
#> residual sum-of-squares: 0
#>
#> Number of iterations to convergence: 3
#> Achieved convergence tolerance: 1.49e-08
### Examples from 'nls.lm' doc
## values over which to simulate data
x <- seq(0,5, length = 100)
## model based on a list of parameters
getPred <- function(parS, xx) parS$a * exp(xx * parS$b) + parS$c
## parameter values used to simulate data
pp <- list(a = 9,b = -1, c = 6)
## simulated data with noise
simDNoisy <- getPred(pp, x) + rnorm(length(x), sd = .1)
## make model
mod <- nlsLM(simDNoisy ~ a * exp(b * x) + c,
start = c(a = 3, b = -0.001, c = 1),
trace = TRUE)
#> It. 0, RSS = 1961.02, Par. = 3 -0.001 1
#> It. 1, RSS = 327.196, Par. = 5.24648 -0.149847 3.23157
#> It. 2, RSS = 103.794, Par. = 6.67486 -0.306651 4.26243
#> It. 3, RSS = 52.5823, Par. = 7.46963 -0.424601 4.69152
#> It. 4, RSS = 32.423, Par. = 7.63317 -0.715042 6.10695
#> It. 5, RSS = 2.92006, Par. = 8.70237 -1.01305 6.18228
#> It. 6, RSS = 0.966151, Par. = 9.00093 -1.00789 5.99787
#> It. 7, RSS = 0.966139, Par. = 9.0009 -1.00801 5.99776
#> It. 8, RSS = 0.966139, Par. = 9.0009 -1.00801 5.99776
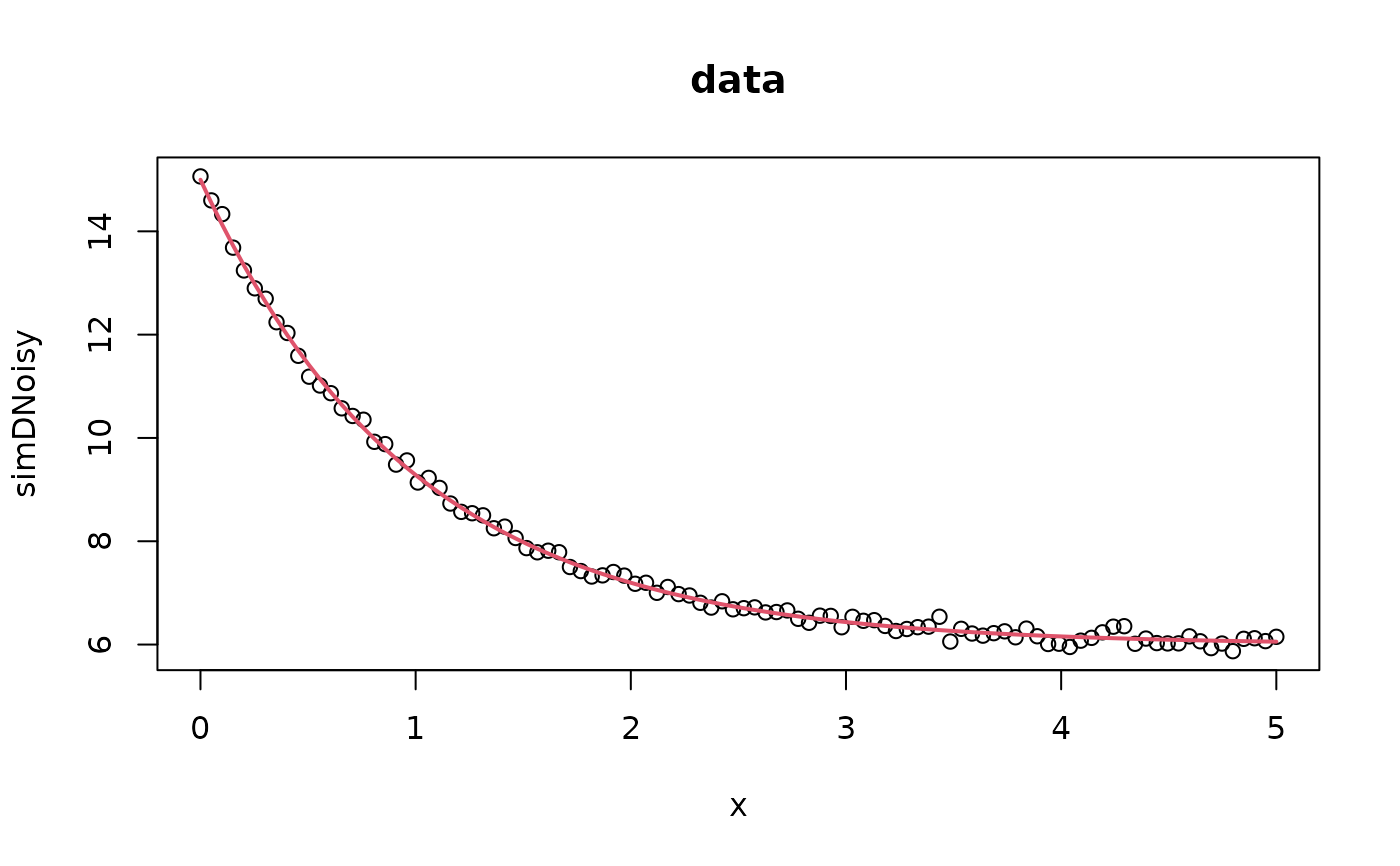
## plot data
plot(x, simDNoisy, main = "data")
## plot fitted values
lines(x, fitted(mod), col = 2, lwd = 2)
 ## create declining cosine
## with noise
TT <- seq(0, 8, length = 501)
tau <- 2.2
N0 <- 1000
a <- 0.25
f0 <- 8
Ndet <- N0 * exp(-TT/tau) * (1 + a * cos(f0 * TT))
N <- Ndet + rnorm(length(Ndet), mean = Ndet, sd = .01 * max(Ndet))
## make model
mod <- nlsLM(N ~ N0 * exp(-TT/tau) * (1 + a * cos(f0 * TT)),
start = c(tau = 2.2, N0 = 1500, a = 0.25, f0 = 10),
trace = TRUE)
#> It. 0, RSS = 2.89784e+07, Par. = 2.2 1500 0.25 10
#> It. 1, RSS = 9.34522e+06, Par. = 2.10369 2040.69 -0.0250233 9.91534
#> It. 2, RSS = 8.80244e+06, Par. = 2.17048 2020.88 0.0505663 10.6983
#> It. 3, RSS = 8.71747e+06, Par. = 2.15925 2027.7 0.0284318 10.5726
#> It. 4, RSS = 8.66794e+06, Par. = 2.16147 2026.61 0.030588 10.3028
#> It. 5, RSS = 8.54227e+06, Par. = 2.16152 2026.39 0.0362254 9.93555
#> It. 6, RSS = 8.1643e+06, Par. = 2.16102 2026.16 0.0480964 9.44405
#> It. 7, RSS = 6.58453e+06, Par. = 2.16039 2025.43 0.0745547 8.7869
#> It. 8, RSS = 1.77669e+06, Par. = 2.16171 2021.76 0.145252 7.88535
#> It. 9, RSS = 212297, Par. = 2.19607 2001.41 0.246896 8.07934
#> It. 10, RSS = 78567.8, Par. = 2.19635 2001.55 0.248848 7.9976
#> It. 11, RSS = 77960.2, Par. = 2.19886 2000.36 0.250807 7.99806
#> It. 12, RSS = 77960.2, Par. = 2.19886 2000.36 0.250807 7.99805
#> It. 13, RSS = 77960.2, Par. = 2.19886 2000.36 0.250807 7.99805
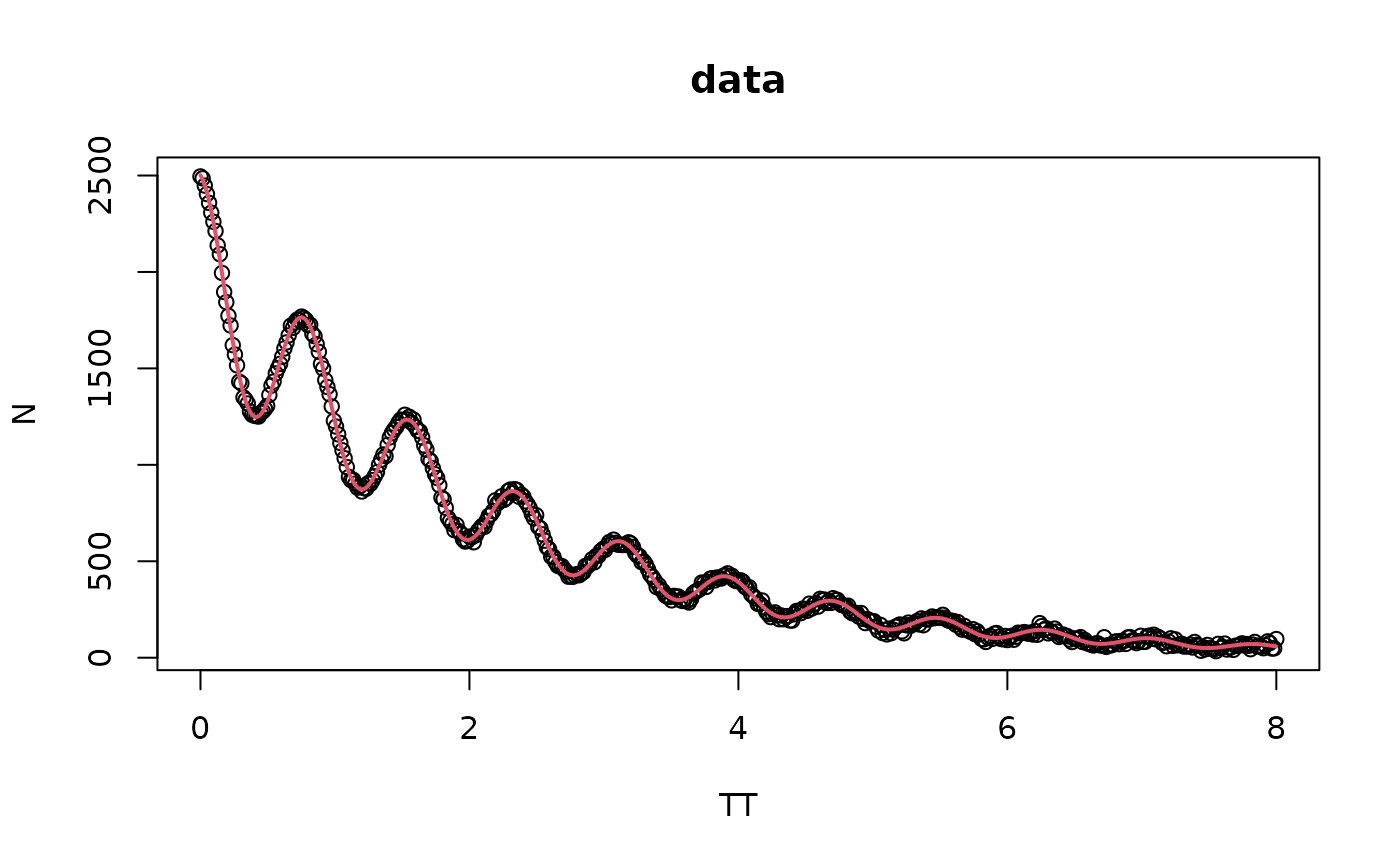
## plot data
plot(TT, N, main = "data")
## plot fitted values
lines(TT, fitted(mod), col = 2, lwd = 2)
## create declining cosine
## with noise
TT <- seq(0, 8, length = 501)
tau <- 2.2
N0 <- 1000
a <- 0.25
f0 <- 8
Ndet <- N0 * exp(-TT/tau) * (1 + a * cos(f0 * TT))
N <- Ndet + rnorm(length(Ndet), mean = Ndet, sd = .01 * max(Ndet))
## make model
mod <- nlsLM(N ~ N0 * exp(-TT/tau) * (1 + a * cos(f0 * TT)),
start = c(tau = 2.2, N0 = 1500, a = 0.25, f0 = 10),
trace = TRUE)
#> It. 0, RSS = 2.89784e+07, Par. = 2.2 1500 0.25 10
#> It. 1, RSS = 9.34522e+06, Par. = 2.10369 2040.69 -0.0250233 9.91534
#> It. 2, RSS = 8.80244e+06, Par. = 2.17048 2020.88 0.0505663 10.6983
#> It. 3, RSS = 8.71747e+06, Par. = 2.15925 2027.7 0.0284318 10.5726
#> It. 4, RSS = 8.66794e+06, Par. = 2.16147 2026.61 0.030588 10.3028
#> It. 5, RSS = 8.54227e+06, Par. = 2.16152 2026.39 0.0362254 9.93555
#> It. 6, RSS = 8.1643e+06, Par. = 2.16102 2026.16 0.0480964 9.44405
#> It. 7, RSS = 6.58453e+06, Par. = 2.16039 2025.43 0.0745547 8.7869
#> It. 8, RSS = 1.77669e+06, Par. = 2.16171 2021.76 0.145252 7.88535
#> It. 9, RSS = 212297, Par. = 2.19607 2001.41 0.246896 8.07934
#> It. 10, RSS = 78567.8, Par. = 2.19635 2001.55 0.248848 7.9976
#> It. 11, RSS = 77960.2, Par. = 2.19886 2000.36 0.250807 7.99806
#> It. 12, RSS = 77960.2, Par. = 2.19886 2000.36 0.250807 7.99805
#> It. 13, RSS = 77960.2, Par. = 2.19886 2000.36 0.250807 7.99805
## plot data
plot(TT, N, main = "data")
## plot fitted values
lines(TT, fitted(mod), col = 2, lwd = 2)