Estimate and display direct and indirect effects of mediators and moderator in path models
mediate.RdFind the direct and indirect effects of a predictor in path models of mediation and moderation. Bootstrap confidence intervals for the indirect effects. Mediation models are just extended regression models making explicit the effect of particular covariates in the model. Moderation is done by multiplication of the predictor variables. This function supplies basic mediation/moderation analyses for some of the classic problem types.
mediate(y, x, m=NULL, data, mod = NULL, z = NULL, n.obs = NULL, use = "pairwise",
n.iter = 5000, alpha = 0.05, std = FALSE,plot=TRUE,zero=TRUE,part=FALSE,
main="Mediation")
mediate.diagram(medi,digits=2,ylim=c(3,7),xlim=c(-1,10),show.c=TRUE,
main="Mediation model",cex=1,l.cex=1,...)
moderate.diagram(medi,digits=2,ylim=c(2,8),main="Moderation model", cex=1,l.cex=1,...)Arguments
- y
The dependent variable (or a formula suitable for a linear model), If a formula, then this is of the form y ~ x +(m) -z (see details)
- x
One or more predictor variables
- m
One (or more) mediating variables
- data
A data frame holding the data or a correlation or covariance matrix.
- mod
A moderating variable, if desired
- z
Variables to partial out, if desired
- n.obs
If the data are from a correlation or covariance matrix, how many observations were used. This will lead to simulated data for the bootstrap.
- use
use="pairwise" is the default when finding correlations or covariances
- n.iter
Number of bootstrap resamplings to conduct
- alpha
Set the width of the confidence interval to be 1 - alpha
- std
standardize the covariances to find the standardized betas
- part
if part=TRUE, find part correlations otherwise find partial correlations when partialling
- plot
Plot the resulting paths
- zero
By default, will zero center the data before doing moderation
- digits
The number of digits to report in the mediate.diagram.
- medi
The output from mediate may be imported into mediate.diagram
- ylim
The limits for the y axis in the mediate and moderate diagram functions
- xlim
The limits for the x axis. Make the minimum more negative if the x by x correlations do not fit.
- show.c
If FALSE, do not draw the c lines, just the partialed (c') lines
- main
The title for the mediate and moderate functions
- cex
Adjust the text size (defaults to 1)
- l.cex
Adjust the text size in arrows, defaults to cex which in turn defaults to 1
- ...
Additional graphical parameters to pass to mediate.diagram
Details
When doing linear modeling, it is frequently convenient to estimate the direct effect of a predictor controlling for the indirect effect of a mediator. See Preacher and Hayes (2004) for a very thorough discussion of mediation. The mediate function will do some basic mediation and moderation models, with bootstrapped confidence intervals for the mediation/moderation effects.
Functionally, this is just regular linear regression and partial correlation with some different output.
In the case of two predictor variables, X and M, and a criterion variable Y, then the direct effect of X on Y, labeled with the path c, is said to be mediated by the effect of x on M (path a) and the effect of M on Y (path b). This partial effect (a b) is said to mediate the direct effect of X –c–> Y: X –a -> M –b–> Y with X –c'–> Y where c' = c - ab.
Testing the significance of the ab mediation effect is done through bootstrapping many random resamples (with replacement) of the data.
For moderation, the moderation effect of Z on the relationship between X -> Y is found by taking the (centered) product of X and Z and then adding this XZ term into the regression. By default, the data are zero centered before doing moderation (product terms). This is following the advice of Cohen, Cohen, West and Aiken (2003). However, to agree with the analyses reported in Hayes (2013) we can set the zero=FALSE option to not zero center the data.
To partial out variables, either define them in the z term, or express as negative entries in the formula mode:
y1 ~ x1 + x2 + (m1)+ (m2) -z will look for the effect of x1 and x2 on y, mediated through m1 and m2 after z is partialled out.
Moderated mediation is done by specifying a product term.
y1 ~ x1 + x2*x3 + (m1)+ (m2) -z will look for the effect of x1, x2, x3 and the product of x2 and x3 on y, mediated through m1 and m2 after z is partialled out.
In the case of being provided just a correlation matrix, the bootstrapped values are based upon bootstrapping from data matching the original covariance/correlation matrix with the addition of normal errors. This allows us to test the mediation/moderation effect even if not given raw data. Moderation can not be done with just correlation matrix.
The function has been tested against some of the basic cases and examples in Hayes (2013) and the associated data sets.
Unless there is a temporal component that allows one to directly distinguish causal paths (time does not reverse direction), interpreting mediation models is problematic. Some people find it useful to compare the differences between mediation models where the causal paths (arrows) are reversed. This is a mistake and should not be done (Thoemmes, 2015).
For fine tuning the size of the graphic output, xlim and ylim can be specified in the mediate.diagram function. Otherwise, the graphics produced by mediate and moderate use the default xlim and ylim values.
Interaction terms (moderation) or mediated moderation can be specified as product terms.
Value
- total
The total direct effect of x on y (c)
- direct
The beta effects of x (c') and m (b) on y
- indirect
The indirect effect of x through m on y (c-ab)
- mean.boot
mean bootstrapped value of indirect effect
- sd.boot
Standard deviation of bootstrapped values
- ci.quant
The upper and lower confidence intervals based upon the quantiles of the bootstrapped distribution.
- boot
The bootstrapped values themselves.
- a
The effect of x on m
- b
The effect of m on y
- b.int
The interaction of x and mod (if specified)
- data
The original data plus the product term (if specified)
References
J. Cohen, P. Cohen, S.G. West, and L.S. Aiken. (2003) Applied multiple regression/correlation analysis for the behavioral sciences. L. Erlbaum Associates, Mahwah, N.J., 3rd ed edition.
Hayes, Andrew F. (2013) Introduction to mediation, moderation, and conditional process analysis: A regression-based approach. Guilford Press.
Preacher, Kristopher J and Hayes, Andrew F (2004) SPSS and SAS procedures for estimating indirect effects in simple mediation models. Behavior Research Methods, Instruments, & Computers 36, (4) 717-731.
Thoemmes, Felix (2015) Reversing arrows in mediation models does not distinguish plausible models. Basic and applied social psychology, 27: 226-234.
Data from Hayes (2013), Preacher and Hayes (2004), and from Kerchoff (1974).
The Tal_Or data set is from Nurit Tal-Or and Jonathan Cohen and Yariv Tsfati and Albert C. Gunther, (2010) “Testing Causal Direction in the Influence of Presumed Media Influence", Communication Research, 37, 801-824 and is used with their kind permission. It is adapted from the webpage of A.F. Hayes. (www.afhayes.com/public/hayes2013data.zip).
The Garcia data set is from Garcia, Donna M. and Schmitt, Michael T. and Branscombe, Nyla R. and Ellemers, Naomi (2010). Women's reactions to ingroup members who protest discriminatory treatment: The importance of beliefs about inequality and response appropriateness. European Journal of Social Psychology, (40) 733-745 and is used with their kind permission. It was downloaded from the Hayes (2013) website.
For an example of how to display the sexism by protest interaction, see the examples in the GSBE (Garcia) data set.
See the “how to do mediation and moderation" at personality-project.org/r/psych/HowTo/mediation.pdf as well as the introductory vignette.
Note
There are a number of other packages that do mediation analysis (e.g., sem and lavaan) and they are probably preferred for more complicated models. This function is supplied for the more basic cases, with 1..k y variables, 1..n x variables, 1 ..j mediators and 1 ..z variables to partial. The number of moderated effects is not limited, but more than 3rd order interactions are not very meaningful. It will not do two step mediation.
The current version will not correctly handle more than one DV.
See also
lmCor and lmCor.diagram for regression and moderation, Garcia for further demonstrations of mediation and moderation.
Examples
# A simple mediation example is the Tal_Or data set (pmi for Hayes)
#The pmi data set from Hayes is available as the Tal_Or data set.
mod4 <- mediate(reaction ~ cond + (pmi), data =Tal_Or,n.iter=50)
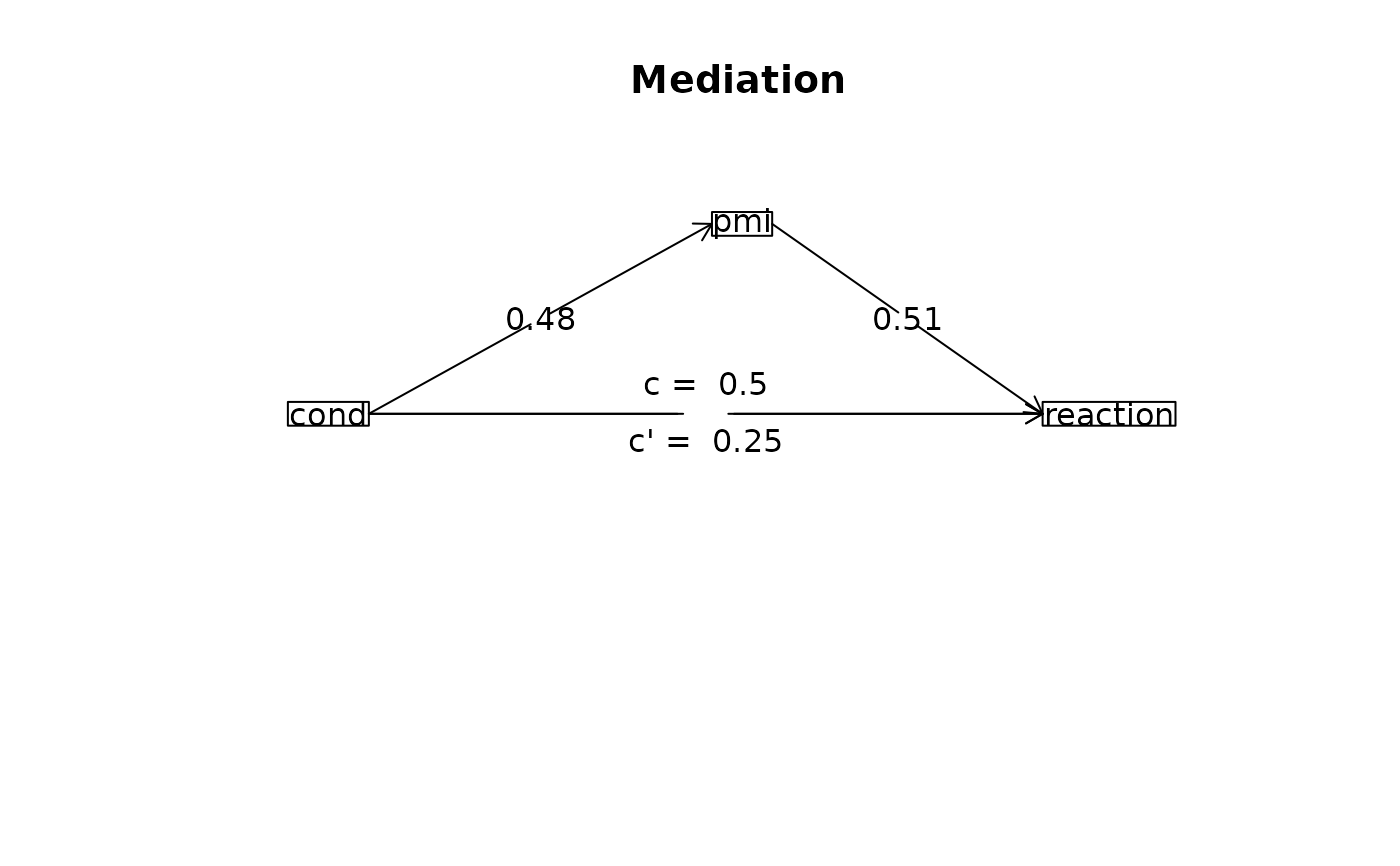 summary(mod4)
#> Call: mediate(y = reaction ~ cond + (pmi), data = Tal_Or, n.iter = 50)
#>
#> Direct effect estimates (traditional regression) (c') X + M on Y
#> reaction se t df Prob
#> Intercept 0.53 0.55 0.96 120 3.40e-01
#> cond 0.25 0.26 0.99 120 3.22e-01
#> pmi 0.51 0.10 5.22 120 7.66e-07
#>
#> R = 0.45 R2 = 0.21 F = 15.56 on 2 and 120 DF p-value: 9.83e-07
#>
#> Total effect estimates (c) (X on Y)
#> reaction se t df Prob
#> Intercept 3.25 0.19 17.05 121 5.68e-34
#> cond 0.50 0.28 1.79 121 7.66e-02
#>
#> 'a' effect estimates (X on M)
#> pmi se t df Prob
#> Intercept 5.38 0.16 33.22 121 1.16e-62
#> cond 0.48 0.24 2.02 121 4.54e-02
#>
#> 'b' effect estimates (M on Y controlling for X)
#> reaction se t df Prob
#> pmi 0.51 0.1 5.22 120 7.66e-07
#>
#> 'ab' effect estimates (through all mediators)
#> reaction boot sd lower upper
#> cond 0.24 0.24 0.13 0.02 0.51
#Two mediators (from Hayes model 6 (chapter 5))
mod6 <- mediate(reaction ~ cond + (pmi) + (import), data =Tal_Or,n.iter=50)
summary(mod4)
#> Call: mediate(y = reaction ~ cond + (pmi), data = Tal_Or, n.iter = 50)
#>
#> Direct effect estimates (traditional regression) (c') X + M on Y
#> reaction se t df Prob
#> Intercept 0.53 0.55 0.96 120 3.40e-01
#> cond 0.25 0.26 0.99 120 3.22e-01
#> pmi 0.51 0.10 5.22 120 7.66e-07
#>
#> R = 0.45 R2 = 0.21 F = 15.56 on 2 and 120 DF p-value: 9.83e-07
#>
#> Total effect estimates (c) (X on Y)
#> reaction se t df Prob
#> Intercept 3.25 0.19 17.05 121 5.68e-34
#> cond 0.50 0.28 1.79 121 7.66e-02
#>
#> 'a' effect estimates (X on M)
#> pmi se t df Prob
#> Intercept 5.38 0.16 33.22 121 1.16e-62
#> cond 0.48 0.24 2.02 121 4.54e-02
#>
#> 'b' effect estimates (M on Y controlling for X)
#> reaction se t df Prob
#> pmi 0.51 0.1 5.22 120 7.66e-07
#>
#> 'ab' effect estimates (through all mediators)
#> reaction boot sd lower upper
#> cond 0.24 0.24 0.13 0.02 0.51
#Two mediators (from Hayes model 6 (chapter 5))
mod6 <- mediate(reaction ~ cond + (pmi) + (import), data =Tal_Or,n.iter=50)
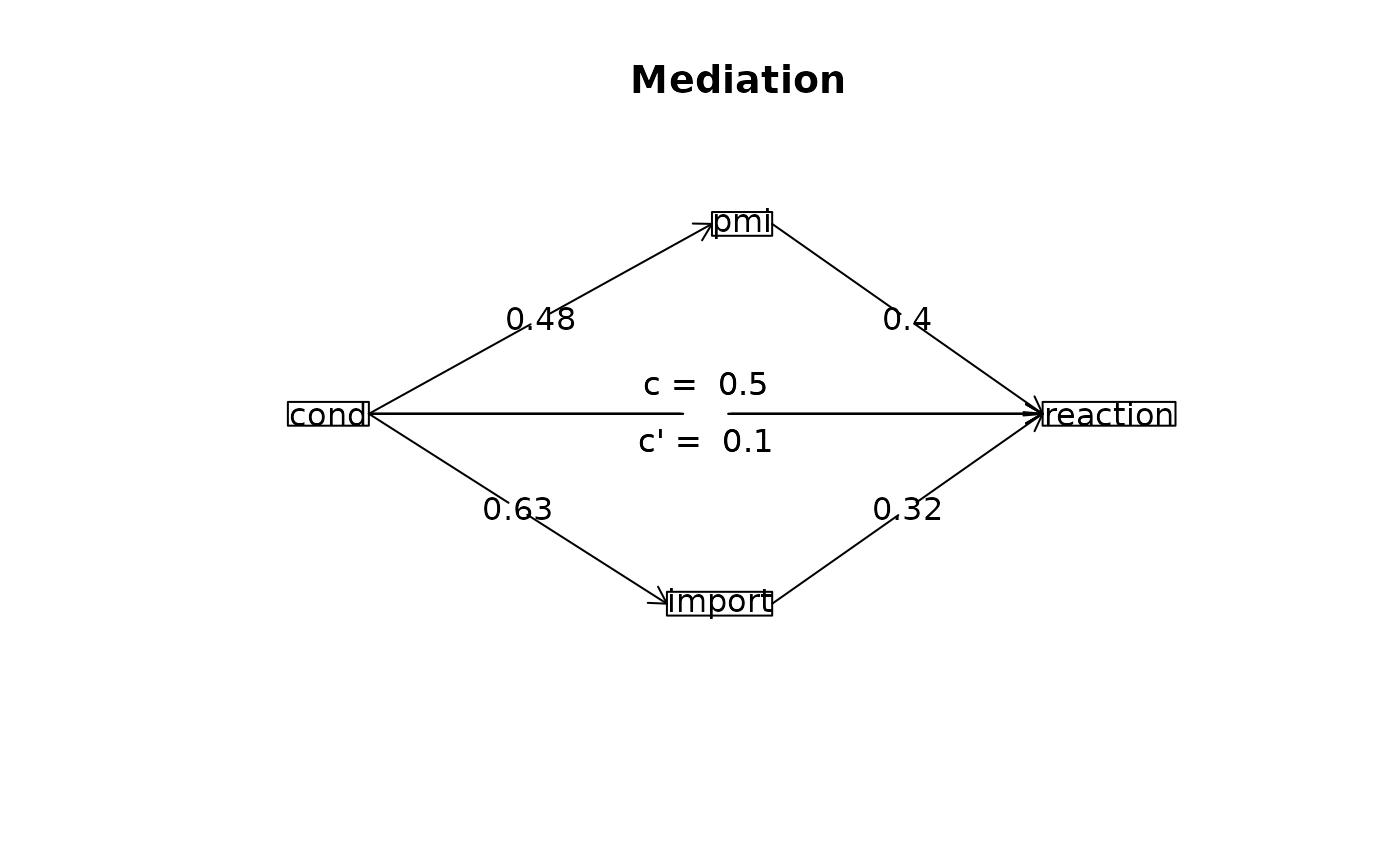 summary(mod6)
#> Call: mediate(y = reaction ~ cond + (pmi) + (import), data = Tal_Or,
#> n.iter = 50)
#>
#> Direct effect estimates (traditional regression) (c') X + M on Y
#> reaction se t df Prob
#> Intercept -0.15 0.53 -0.28 119 7.78e-01
#> cond 0.10 0.24 0.43 119 6.66e-01
#> pmi 0.40 0.09 4.26 119 4.04e-05
#> import 0.32 0.07 4.59 119 1.13e-05
#>
#> R = 0.57 R2 = 0.33 F = 19.11 on 3 and 119 DF p-value: 3.5e-10
#>
#> Total effect estimates (c) (X on Y)
#> reaction se t df Prob
#> Intercept 3.25 0.19 17.05 121 5.68e-34
#> cond 0.50 0.28 1.79 121 7.66e-02
#>
#> 'a' effect estimates (X on M)
#> pmi se t df Prob
#> Intercept 5.38 0.16 33.22 121 1.16e-62
#> cond 0.48 0.24 2.02 121 4.54e-02
#> import se t df Prob
#> Intercept 3.91 0.21 18.37 121 8.39e-37
#> cond 0.63 0.31 2.02 121 4.52e-02
#>
#> 'b' effect estimates (M on Y controlling for X)
#> reaction se t df Prob
#> pmi 0.40 0.09 4.26 119 4.04e-05
#> import 0.32 0.07 4.59 119 1.13e-05
#>
#> 'ab' effect estimates (through all mediators)
#> reaction boot sd lower upper
#> cond 0.39 0.35 0.15 0.1 0.62
#>
#> 'ab' effects estimates for each mediator for reaction
#> boot sd lower upper
#> cond 0.35 0.15 0.10 0.62
#> pmi*cond 0.18 0.09 0.04 0.34
#> import*cond 0.17 0.11 -0.03 0.39
#Moderated mediation is done for the Garcia (Garcia, 2010) data set.
# (see Hayes, 2013 for the protest data set
#n.iter set to 50 (instead of default of 5000) for speed of example
#no mediation, just an interaction
mod7 <- mediate(liking ~ sexism * prot2 , data=Garcia, n.iter = 50)
summary(mod6)
#> Call: mediate(y = reaction ~ cond + (pmi) + (import), data = Tal_Or,
#> n.iter = 50)
#>
#> Direct effect estimates (traditional regression) (c') X + M on Y
#> reaction se t df Prob
#> Intercept -0.15 0.53 -0.28 119 7.78e-01
#> cond 0.10 0.24 0.43 119 6.66e-01
#> pmi 0.40 0.09 4.26 119 4.04e-05
#> import 0.32 0.07 4.59 119 1.13e-05
#>
#> R = 0.57 R2 = 0.33 F = 19.11 on 3 and 119 DF p-value: 3.5e-10
#>
#> Total effect estimates (c) (X on Y)
#> reaction se t df Prob
#> Intercept 3.25 0.19 17.05 121 5.68e-34
#> cond 0.50 0.28 1.79 121 7.66e-02
#>
#> 'a' effect estimates (X on M)
#> pmi se t df Prob
#> Intercept 5.38 0.16 33.22 121 1.16e-62
#> cond 0.48 0.24 2.02 121 4.54e-02
#> import se t df Prob
#> Intercept 3.91 0.21 18.37 121 8.39e-37
#> cond 0.63 0.31 2.02 121 4.52e-02
#>
#> 'b' effect estimates (M on Y controlling for X)
#> reaction se t df Prob
#> pmi 0.40 0.09 4.26 119 4.04e-05
#> import 0.32 0.07 4.59 119 1.13e-05
#>
#> 'ab' effect estimates (through all mediators)
#> reaction boot sd lower upper
#> cond 0.39 0.35 0.15 0.1 0.62
#>
#> 'ab' effects estimates for each mediator for reaction
#> boot sd lower upper
#> cond 0.35 0.15 0.10 0.62
#> pmi*cond 0.18 0.09 0.04 0.34
#> import*cond 0.17 0.11 -0.03 0.39
#Moderated mediation is done for the Garcia (Garcia, 2010) data set.
# (see Hayes, 2013 for the protest data set
#n.iter set to 50 (instead of default of 5000) for speed of example
#no mediation, just an interaction
mod7 <- mediate(liking ~ sexism * prot2 , data=Garcia, n.iter = 50)
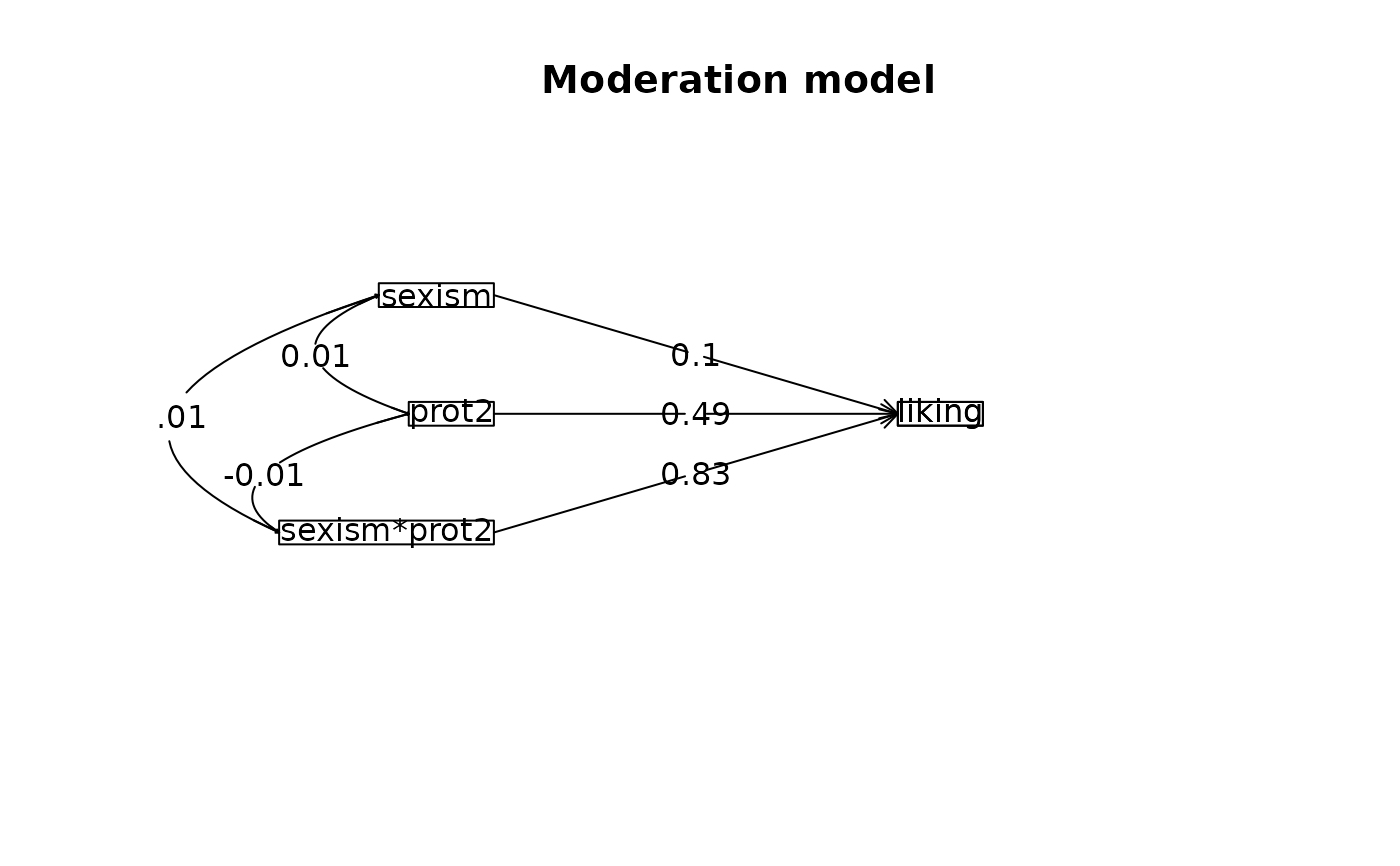 summary(mod7)
#> Call: mediate(y = liking ~ sexism * prot2, data = Garcia, n.iter = 50)
#>
#> No mediator specified leads to traditional regression
#> liking se t df Prob
#> Intercept -0.01 0.09 -0.14 125 0.88900
#> sexism 0.10 0.11 0.86 125 0.39100
#> prot2 0.49 0.19 2.63 125 0.00958
#> sexism*prot2 0.83 0.24 3.42 125 0.00084
#>
#> R = 0.37 R2 = 0.13 F = 6.42 on 3 and 125 DF p-value: 0.000444
data(GSBE) #The Garcia et al data set (aka GSBE)
mod11.4 <- mediate(liking ~ sexism * prot2 + (respappr), data=Garcia,
n.iter = 50,zero=FALSE) #to match Hayes
summary(mod7)
#> Call: mediate(y = liking ~ sexism * prot2, data = Garcia, n.iter = 50)
#>
#> No mediator specified leads to traditional regression
#> liking se t df Prob
#> Intercept -0.01 0.09 -0.14 125 0.88900
#> sexism 0.10 0.11 0.86 125 0.39100
#> prot2 0.49 0.19 2.63 125 0.00958
#> sexism*prot2 0.83 0.24 3.42 125 0.00084
#>
#> R = 0.37 R2 = 0.13 F = 6.42 on 3 and 125 DF p-value: 0.000444
data(GSBE) #The Garcia et al data set (aka GSBE)
mod11.4 <- mediate(liking ~ sexism * prot2 + (respappr), data=Garcia,
n.iter = 50,zero=FALSE) #to match Hayes
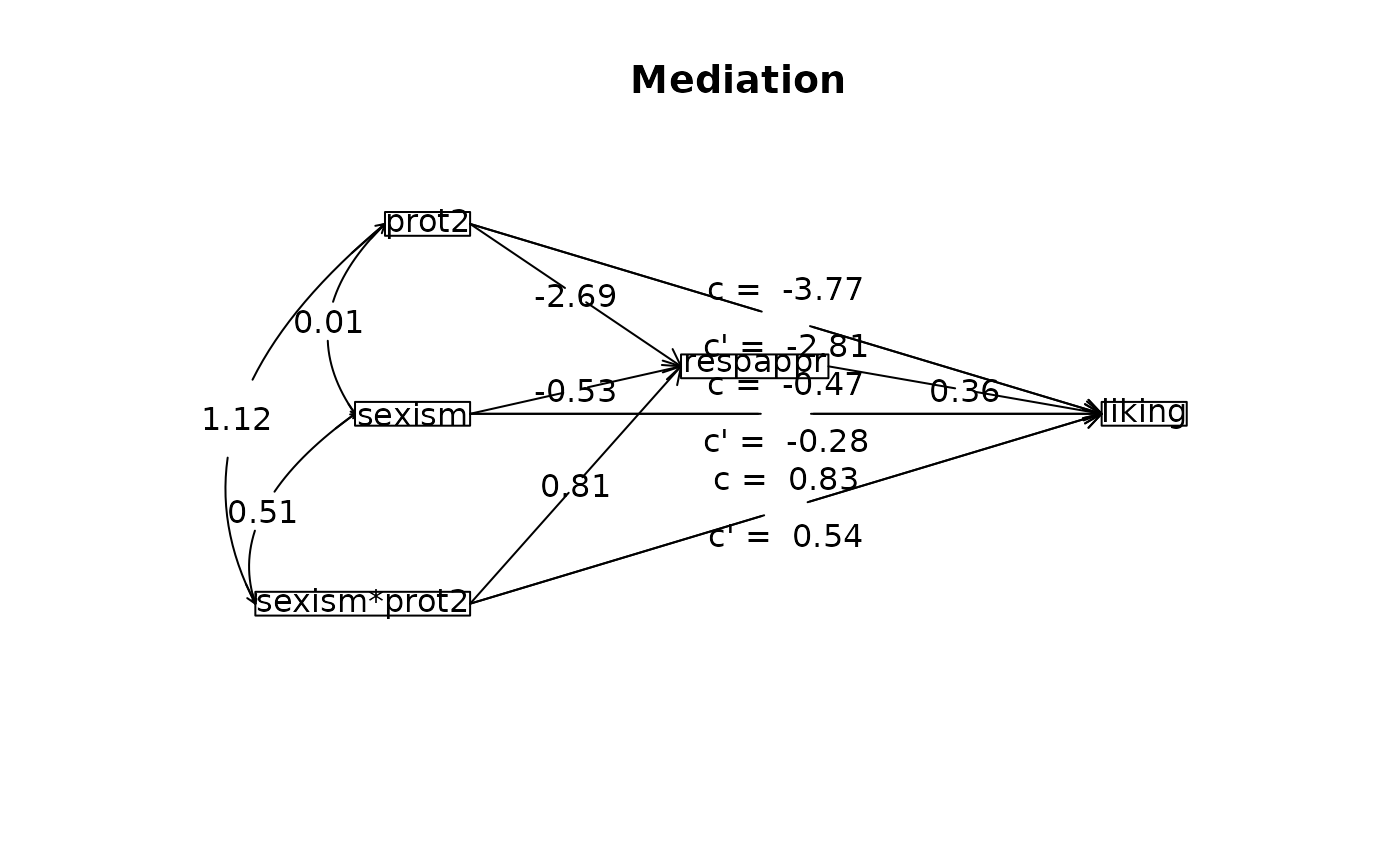 summary(mod11.4)
#> Call: mediate(y = liking ~ sexism * prot2 + (respappr), data = Garcia,
#> n.iter = 50, zero = FALSE)
#>
#> Direct effect estimates (traditional regression) (c') X + M on Y
#> liking se t df Prob
#> Intercept 5.35 1.06 5.04 124 1.60e-06
#> sexism -0.28 0.19 -1.49 124 1.39e-01
#> prot2 -2.81 1.16 -2.42 124 1.70e-02
#> sexism*prot2 0.54 0.23 2.36 124 1.97e-02
#> respappr 0.36 0.07 5.09 124 1.28e-06
#>
#> R = 0.53 R2 = 0.28 F = 12.26 on 4 and 124 DF p-value: 1.99e-08
#>
#> Total effect estimates (c) (X on Y)
#> liking se t df Prob
#> Intercept 7.71 1.04 7.37 125 1.99e-11
#> sexism -0.47 0.20 -2.32 125 2.20e-02
#> prot2 -3.77 1.25 -3.01 125 3.18e-03
#> sexism*prot2 0.83 0.24 3.42 125 8.40e-04
#>
#> 'a' effect estimates (X on M)
#> respappr se t df Prob
#> Intercept 6.57 1.21 5.43 125 2.83e-07
#> sexism -0.53 0.24 -2.24 125 2.67e-02
#> prot2 -2.69 1.45 -1.85 125 6.65e-02
#> sexism*prot2 0.81 0.28 2.87 125 4.78e-03
#>
#> 'b' effect estimates (M on Y controlling for X)
#> liking se t df Prob
#> respappr 0.36 0.07 5.09 124 1.28e-06
#>
#> 'ab' effect estimates (through all mediators)
#> liking boot sd lower upper
#> sexism -0.19 -0.19 0.12 -0.41 0
#> prot2 -0.97 -1.02 0.69 -0.41 0
#> sexism*prot2 0.29 0.30 0.14 -0.41 0
#to see this interaction graphically, run the examples in ?Garcia
#Simulated data from Preacher and Hayes (2004)
sobel <- structure(list(SATIS = c(-0.59, 1.3, 0.02, 0.01, 0.79, -0.35,
-0.03, 1.75, -0.8, -1.2, -1.27, 0.7, -1.59, 0.68, -0.39, 1.33,
-1.59, 1.34, 0.1, 0.05, 0.66, 0.56, 0.85, 0.88, 0.14, -0.72,
0.84, -1.13, -0.13, 0.2), THERAPY = structure(c(0, 1, 1, 0, 1,
1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1,
1, 1, 1, 0), value.labels = structure(c(1, 0), .Names = c("cognitive",
"standard"))), ATTRIB = c(-1.17, 0.04, 0.58, -0.23, 0.62, -0.26,
-0.28, 0.52, 0.34, -0.09, -1.09, 1.05, -1.84, -0.95, 0.15, 0.07,
-0.1, 2.35, 0.75, 0.49, 0.67, 1.21, 0.31, 1.97, -0.94, 0.11,
-0.54, -0.23, 0.05, -1.07)), .Names = c("SATIS", "THERAPY", "ATTRIB"
), row.names = c(NA, -30L), class = "data.frame", variable.labels = structure(c("Satisfaction",
"Therapy", "Attributional Positivity"), .Names = c("SATIS", "THERAPY",
"ATTRIB")))
#n.iter set to 50 (instead of default of 5000) for speed of example
#There are several forms of input. The original specified y, x , and the mediator
#mediate(1,2,3,sobel,n.iter=50) #The example in Preacher and Hayes
#As of October, 2017 we can specify this in a formula mode
mediate (SATIS ~ THERAPY + (ATTRIB),data=sobel, n.iter=50) #specify the mediator by
summary(mod11.4)
#> Call: mediate(y = liking ~ sexism * prot2 + (respappr), data = Garcia,
#> n.iter = 50, zero = FALSE)
#>
#> Direct effect estimates (traditional regression) (c') X + M on Y
#> liking se t df Prob
#> Intercept 5.35 1.06 5.04 124 1.60e-06
#> sexism -0.28 0.19 -1.49 124 1.39e-01
#> prot2 -2.81 1.16 -2.42 124 1.70e-02
#> sexism*prot2 0.54 0.23 2.36 124 1.97e-02
#> respappr 0.36 0.07 5.09 124 1.28e-06
#>
#> R = 0.53 R2 = 0.28 F = 12.26 on 4 and 124 DF p-value: 1.99e-08
#>
#> Total effect estimates (c) (X on Y)
#> liking se t df Prob
#> Intercept 7.71 1.04 7.37 125 1.99e-11
#> sexism -0.47 0.20 -2.32 125 2.20e-02
#> prot2 -3.77 1.25 -3.01 125 3.18e-03
#> sexism*prot2 0.83 0.24 3.42 125 8.40e-04
#>
#> 'a' effect estimates (X on M)
#> respappr se t df Prob
#> Intercept 6.57 1.21 5.43 125 2.83e-07
#> sexism -0.53 0.24 -2.24 125 2.67e-02
#> prot2 -2.69 1.45 -1.85 125 6.65e-02
#> sexism*prot2 0.81 0.28 2.87 125 4.78e-03
#>
#> 'b' effect estimates (M on Y controlling for X)
#> liking se t df Prob
#> respappr 0.36 0.07 5.09 124 1.28e-06
#>
#> 'ab' effect estimates (through all mediators)
#> liking boot sd lower upper
#> sexism -0.19 -0.19 0.12 -0.41 0
#> prot2 -0.97 -1.02 0.69 -0.41 0
#> sexism*prot2 0.29 0.30 0.14 -0.41 0
#to see this interaction graphically, run the examples in ?Garcia
#Simulated data from Preacher and Hayes (2004)
sobel <- structure(list(SATIS = c(-0.59, 1.3, 0.02, 0.01, 0.79, -0.35,
-0.03, 1.75, -0.8, -1.2, -1.27, 0.7, -1.59, 0.68, -0.39, 1.33,
-1.59, 1.34, 0.1, 0.05, 0.66, 0.56, 0.85, 0.88, 0.14, -0.72,
0.84, -1.13, -0.13, 0.2), THERAPY = structure(c(0, 1, 1, 0, 1,
1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1,
1, 1, 1, 0), value.labels = structure(c(1, 0), .Names = c("cognitive",
"standard"))), ATTRIB = c(-1.17, 0.04, 0.58, -0.23, 0.62, -0.26,
-0.28, 0.52, 0.34, -0.09, -1.09, 1.05, -1.84, -0.95, 0.15, 0.07,
-0.1, 2.35, 0.75, 0.49, 0.67, 1.21, 0.31, 1.97, -0.94, 0.11,
-0.54, -0.23, 0.05, -1.07)), .Names = c("SATIS", "THERAPY", "ATTRIB"
), row.names = c(NA, -30L), class = "data.frame", variable.labels = structure(c("Satisfaction",
"Therapy", "Attributional Positivity"), .Names = c("SATIS", "THERAPY",
"ATTRIB")))
#n.iter set to 50 (instead of default of 5000) for speed of example
#There are several forms of input. The original specified y, x , and the mediator
#mediate(1,2,3,sobel,n.iter=50) #The example in Preacher and Hayes
#As of October, 2017 we can specify this in a formula mode
mediate (SATIS ~ THERAPY + (ATTRIB),data=sobel, n.iter=50) #specify the mediator by
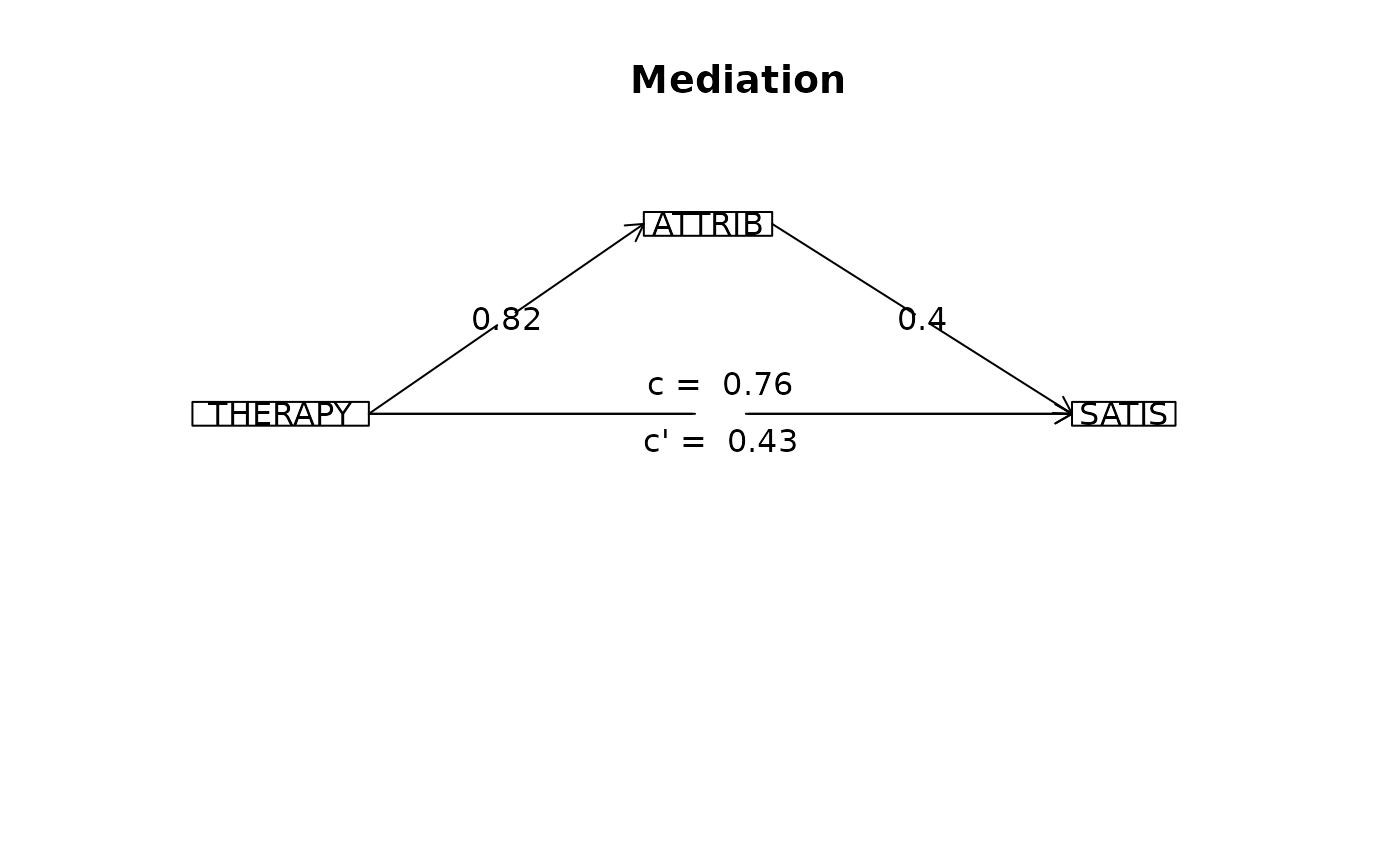 #>
#> Mediation/Moderation Analysis
#> Call: mediate(y = SATIS ~ THERAPY + (ATTRIB), data = sobel, n.iter = 50)
#>
#> The DV (Y) was SATIS . The IV (X) was THERAPY . The mediating variable(s) = ATTRIB .
#>
#> Total effect(c) of THERAPY on SATIS = 0.76 S.E. = 0.31 t = 2.5 df= 28 with p = 0.019
#> Direct effect (c') of THERAPY on SATIS removing ATTRIB = 0.43 S.E. = 0.32 t = 1.35 df= 27 with p = 0.19
#> Indirect effect (ab) of THERAPY on SATIS through ATTRIB = 0.33
#> Mean bootstrapped indirect effect = 0.29 with standard error = 0.14 Lower CI = 0.03 Upper CI = 0.51
#> R = 0.56 R2 = 0.31 F = 6.06 on 2 and 27 DF p-value: 0.00272
#>
#> To see the longer output, specify short = FALSE in the print statement or ask for the summary
# adding parentheses
#A.C. Kerchoff, (1974) Ambition and Attainment: A Study of Four Samples of American Boys.
#Data from sem package taken from Kerckhoff (and in turn, from Lisrel manual)
R.kerch <- structure(list(Intelligence = c(1, -0.1, 0.277, 0.25, 0.572,
0.489, 0.335), Siblings = c(-0.1, 1, -0.152, -0.108, -0.105,
-0.213, -0.153), FatherEd = c(0.277, -0.152, 1, 0.611, 0.294,
0.446, 0.303), FatherOcc = c(0.25, -0.108, 0.611, 1, 0.248, 0.41,
0.331), Grades = c(0.572, -0.105, 0.294, 0.248, 1, 0.597, 0.478
), EducExp = c(0.489, -0.213, 0.446, 0.41, 0.597, 1, 0.651),
OccupAsp = c(0.335, -0.153, 0.303, 0.331, 0.478, 0.651, 1
)), .Names = c("Intelligence", "Siblings", "FatherEd", "FatherOcc",
"Grades", "EducExp", "OccupAsp"), class = "data.frame", row.names = c("Intelligence",
"Siblings", "FatherEd", "FatherOcc", "Grades", "EducExp", "OccupAsp"
))
#n.iter set to 50 (instead of default of 5000) for speed of demo
#mod.k <- mediate("OccupAsp","Intelligence",m= c(2:5),data=R.kerch,n.obs=767,n.iter=50)
#new style
mod.k <- mediate(OccupAsp ~ Intelligence + (Siblings) + (FatherEd) + (FatherOcc) +
(Grades), data = R.kerch, n.obs=767, n.iter=50)
#> The replication data matrices were simulated based upon the specified number of subjects and the observed correlation matrix.
#>
#> Mediation/Moderation Analysis
#> Call: mediate(y = SATIS ~ THERAPY + (ATTRIB), data = sobel, n.iter = 50)
#>
#> The DV (Y) was SATIS . The IV (X) was THERAPY . The mediating variable(s) = ATTRIB .
#>
#> Total effect(c) of THERAPY on SATIS = 0.76 S.E. = 0.31 t = 2.5 df= 28 with p = 0.019
#> Direct effect (c') of THERAPY on SATIS removing ATTRIB = 0.43 S.E. = 0.32 t = 1.35 df= 27 with p = 0.19
#> Indirect effect (ab) of THERAPY on SATIS through ATTRIB = 0.33
#> Mean bootstrapped indirect effect = 0.29 with standard error = 0.14 Lower CI = 0.03 Upper CI = 0.51
#> R = 0.56 R2 = 0.31 F = 6.06 on 2 and 27 DF p-value: 0.00272
#>
#> To see the longer output, specify short = FALSE in the print statement or ask for the summary
# adding parentheses
#A.C. Kerchoff, (1974) Ambition and Attainment: A Study of Four Samples of American Boys.
#Data from sem package taken from Kerckhoff (and in turn, from Lisrel manual)
R.kerch <- structure(list(Intelligence = c(1, -0.1, 0.277, 0.25, 0.572,
0.489, 0.335), Siblings = c(-0.1, 1, -0.152, -0.108, -0.105,
-0.213, -0.153), FatherEd = c(0.277, -0.152, 1, 0.611, 0.294,
0.446, 0.303), FatherOcc = c(0.25, -0.108, 0.611, 1, 0.248, 0.41,
0.331), Grades = c(0.572, -0.105, 0.294, 0.248, 1, 0.597, 0.478
), EducExp = c(0.489, -0.213, 0.446, 0.41, 0.597, 1, 0.651),
OccupAsp = c(0.335, -0.153, 0.303, 0.331, 0.478, 0.651, 1
)), .Names = c("Intelligence", "Siblings", "FatherEd", "FatherOcc",
"Grades", "EducExp", "OccupAsp"), class = "data.frame", row.names = c("Intelligence",
"Siblings", "FatherEd", "FatherOcc", "Grades", "EducExp", "OccupAsp"
))
#n.iter set to 50 (instead of default of 5000) for speed of demo
#mod.k <- mediate("OccupAsp","Intelligence",m= c(2:5),data=R.kerch,n.obs=767,n.iter=50)
#new style
mod.k <- mediate(OccupAsp ~ Intelligence + (Siblings) + (FatherEd) + (FatherOcc) +
(Grades), data = R.kerch, n.obs=767, n.iter=50)
#> The replication data matrices were simulated based upon the specified number of subjects and the observed correlation matrix.
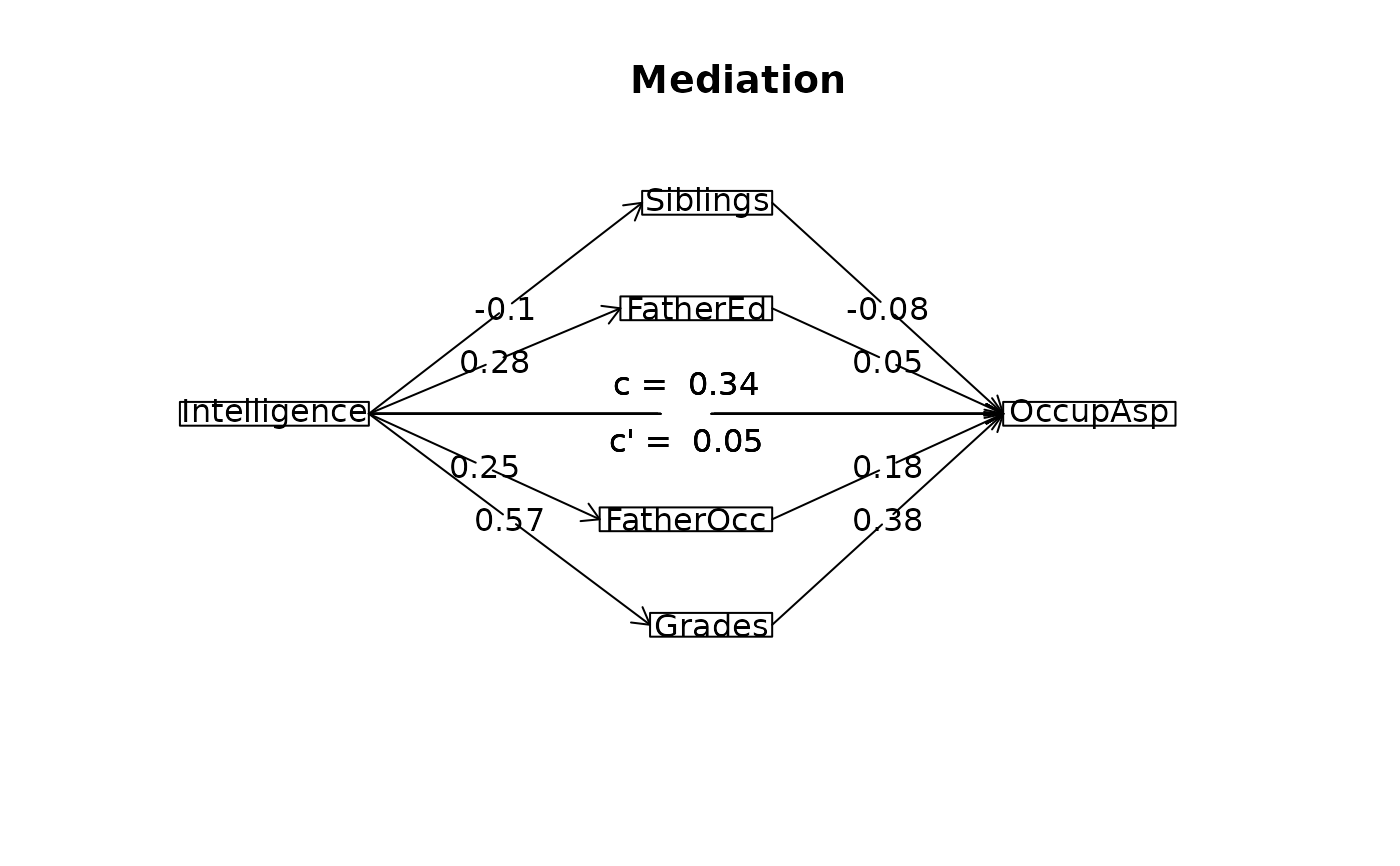 mediate.diagram(mod.k)
mediate.diagram(mod.k)
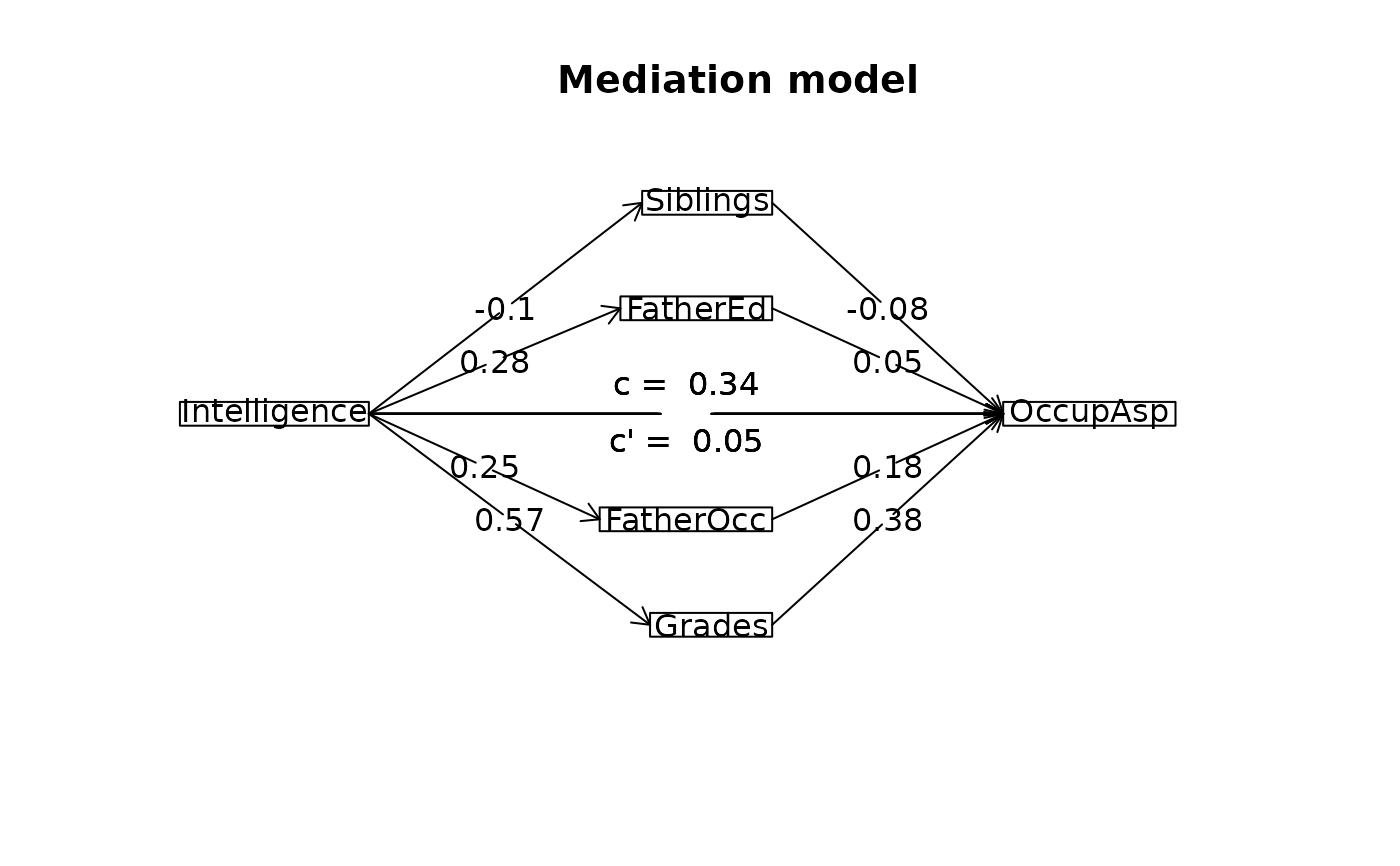 #print the path values
mod.k
#>
#> Mediation/Moderation Analysis
#> Call: mediate(y = OccupAsp ~ Intelligence + (Siblings) + (FatherEd) +
#> (FatherOcc) + (Grades), data = R.kerch, n.obs = 767, n.iter = 50)
#>
#> The DV (Y) was OccupAsp . The IV (X) was Intelligence . The mediating variable(s) = Siblings FatherEd FatherOcc Grades .
#>
#> Total effect(c) of Intelligence on OccupAsp = 0.34 S.E. = 0.03 t = 9.83 df= 765 with p = 1.4e-21
#> Direct effect (c') of Intelligence on OccupAsp removing Siblings FatherEd FatherOcc Grades = 0.05 S.E. = 0.04 t = 1.29 df= 761 with p = 0.2
#> Indirect effect (ab) of Intelligence on OccupAsp through Siblings FatherEd FatherOcc Grades = 0.29
#> Mean bootstrapped indirect effect = 0.32 with standard error = 0.02 Lower CI = 0.27 Upper CI = 0.36
#> R = 0.54 R2 = 0.29 F = 61.36 on 5 and 761 DF p-value: 4.85e-62
#>
#> To see the longer output, specify short = FALSE in the print statement or ask for the summary
#Compare the following solution to the path coefficients found by the sem package
#mod.k2 <- mediate(y="OccupAsp",x=c("Intelligence","Siblings","FatherEd","FatherOcc"),
# m= c(5:6),data=R.kerch,n.obs=767,n.iter=50)
#new format
mod.k2 <- mediate(OccupAsp ~ Intelligence + Siblings + FatherEd + FatherOcc + (Grades) +
(EducExp),data=R.kerch, n.obs=767, n.iter=50)
#> The replication data matrices were simulated based upon the specified number of subjects and the observed correlation matrix.
#print the path values
mod.k
#>
#> Mediation/Moderation Analysis
#> Call: mediate(y = OccupAsp ~ Intelligence + (Siblings) + (FatherEd) +
#> (FatherOcc) + (Grades), data = R.kerch, n.obs = 767, n.iter = 50)
#>
#> The DV (Y) was OccupAsp . The IV (X) was Intelligence . The mediating variable(s) = Siblings FatherEd FatherOcc Grades .
#>
#> Total effect(c) of Intelligence on OccupAsp = 0.34 S.E. = 0.03 t = 9.83 df= 765 with p = 1.4e-21
#> Direct effect (c') of Intelligence on OccupAsp removing Siblings FatherEd FatherOcc Grades = 0.05 S.E. = 0.04 t = 1.29 df= 761 with p = 0.2
#> Indirect effect (ab) of Intelligence on OccupAsp through Siblings FatherEd FatherOcc Grades = 0.29
#> Mean bootstrapped indirect effect = 0.32 with standard error = 0.02 Lower CI = 0.27 Upper CI = 0.36
#> R = 0.54 R2 = 0.29 F = 61.36 on 5 and 761 DF p-value: 4.85e-62
#>
#> To see the longer output, specify short = FALSE in the print statement or ask for the summary
#Compare the following solution to the path coefficients found by the sem package
#mod.k2 <- mediate(y="OccupAsp",x=c("Intelligence","Siblings","FatherEd","FatherOcc"),
# m= c(5:6),data=R.kerch,n.obs=767,n.iter=50)
#new format
mod.k2 <- mediate(OccupAsp ~ Intelligence + Siblings + FatherEd + FatherOcc + (Grades) +
(EducExp),data=R.kerch, n.obs=767, n.iter=50)
#> The replication data matrices were simulated based upon the specified number of subjects and the observed correlation matrix.
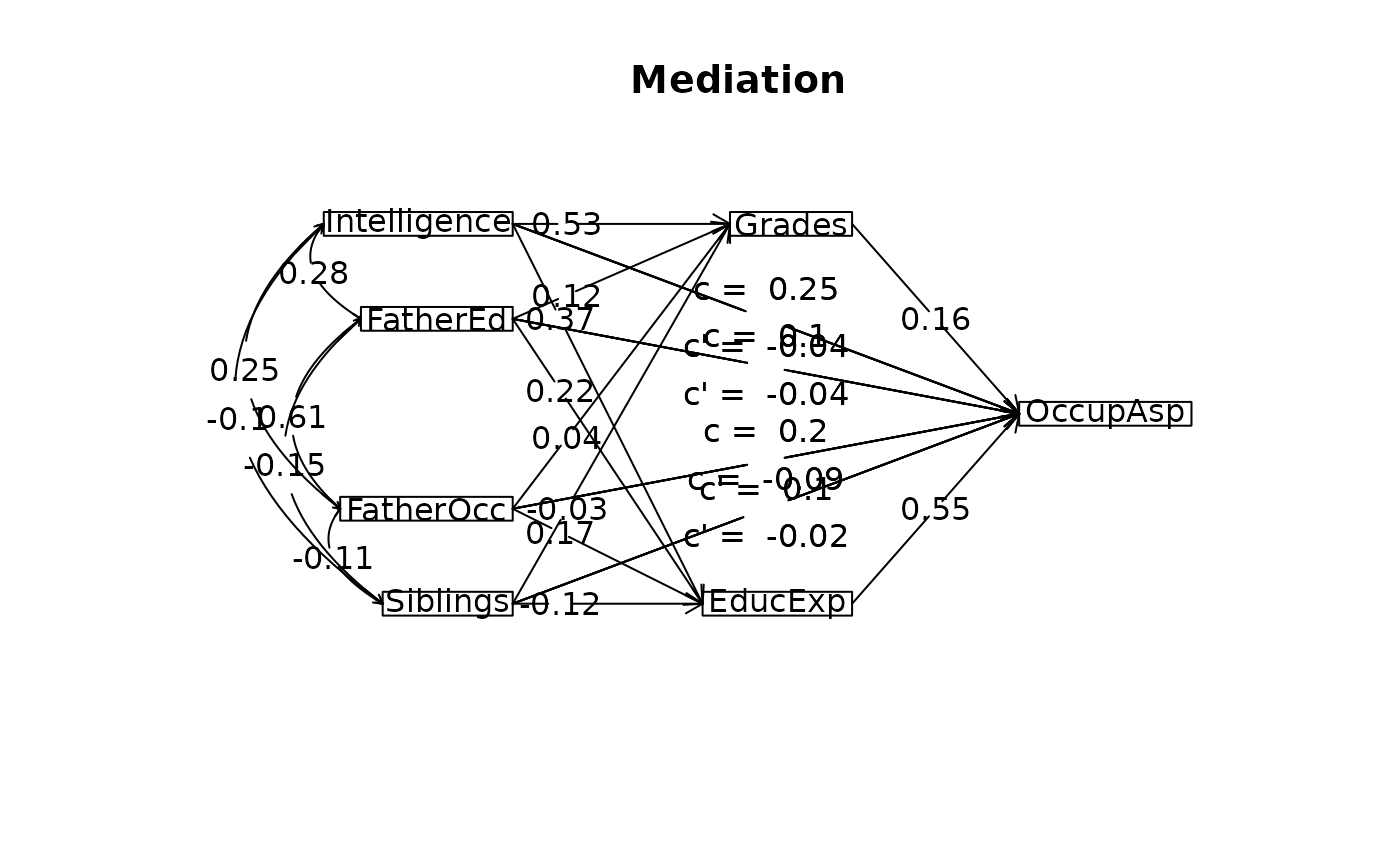 mediate.diagram(mod.k2,show.c=FALSE) #simpler output
mediate.diagram(mod.k2,show.c=FALSE) #simpler output
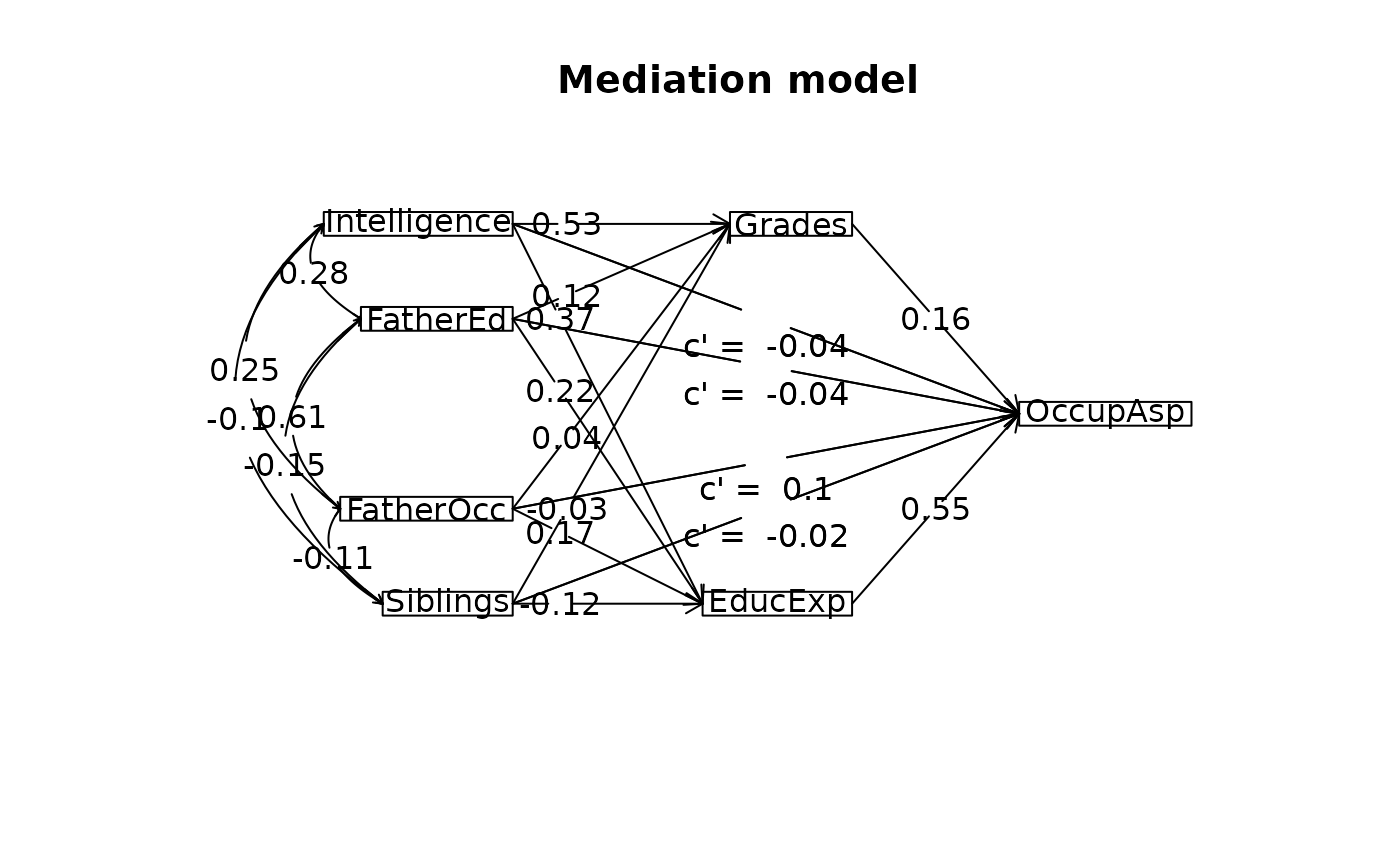 #print the path values
mod.k2
#>
#> Mediation/Moderation Analysis
#> Call: mediate(y = OccupAsp ~ Intelligence + Siblings + FatherEd + FatherOcc +
#> (Grades) + (EducExp), data = R.kerch, n.obs = 767, n.iter = 50)
#>
#> The DV (Y) was OccupAsp . The IV (X) was Intelligence Siblings FatherEd FatherOcc . The mediating variable(s) = Grades EducExp .
#>
#> Total effect(c) of Intelligence on OccupAsp = 0.25 S.E. = 0.03 t = 7.29 df= 762 with p = 7.6e-13
#> Direct effect (c') of Intelligence on OccupAsp removing Grades EducExp = -0.04 S.E. = 0.03 t = -1.16 df= 760 with p = 0.25
#> Indirect effect (ab) of Intelligence on OccupAsp through Grades EducExp = 0.29
#> Mean bootstrapped indirect effect = 0.32 with standard error = 0.03 Lower CI = 0.27 Upper CI = 0.37
#>
#> Total effect(c) of Siblings on OccupAsp = -0.09 S.E. = 0.03 t = -2.78 df= 762 with p = 0.0056
#> Direct effect (c') of Siblings on OccupAsp removing Grades EducExp = -0.02 S.E. = 0.03 t = -0.68 df= 760 with p = 0.5
#> Indirect effect (ab) of Siblings on OccupAsp through Grades EducExp = -0.07
#> Mean bootstrapped indirect effect = -0.07 with standard error = 0.02 Lower CI = -0.1 Upper CI = -0.04
#>
#> Total effect(c) of FatherEd on OccupAsp = 0.1 S.E. = 0.04 t = 2.36 df= 762 with p = 0.018
#> Direct effect (c') of FatherEd on OccupAsp removing Grades EducExp = -0.04 S.E. = 0.04 t = -1.16 df= 760 with p = 0.25
#> Indirect effect (ab) of FatherEd on OccupAsp through Grades EducExp = 0.14
#> Mean bootstrapped indirect effect = 0.13 with standard error = 0.02 Lower CI = 0.09 Upper CI = 0.19
#>
#> Total effect(c) of FatherOcc on OccupAsp = 0.2 S.E. = 0.04 t = 4.8 df= 762 with p = 1.9e-06
#> Direct effect (c') of FatherOcc on OccupAsp removing Grades EducExp = 0.1 S.E. = 0.03 t = 2.85 df= 760 with p = 0.0044
#> Indirect effect (ab) of FatherOcc on OccupAsp through Grades EducExp = 0.1
#> Mean bootstrapped indirect effect = 0.11 with standard error = 0.03 Lower CI = 0.06 Upper CI = 0.15
#> R = 0.67 R2 = 0.44 F = 100.9 on 6 and 760 DF p-value: 4.88e-104
#>
#> To see the longer output, specify short = FALSE in the print statement or ask for the summary
#Several interesting test cases are taken from analyses of the Spengler data set
#This is temporarily added to psych from psychTools to help build for CRAN
#Although the sample sizes are actually very large in the first wave, I use the
#sample sizes from the last wave
#We set the n.iter to be 50 instead of the default value of 5,000
if(require("psychTools")) {
mod1 <- mediate(Income.50 ~ IQ + Parental+ (Ed.11) ,data=Spengler,
n.obs = 1952, n.iter=50)
mod2 <- mediate(Income.50 ~ IQ + Parental+ (Ed.11) + (Income.11)
,data=Spengler,n.obs = 1952, n.iter=50)
#Now, compare these models
anova(mod1,mod2)
#Current version does not support two DVs
#mod22 <- mediate(Income.50 + Educ.50 ~ IQ + Parental+ (Ed.11) + (Income.11)
# ,data=Spengler,n.obs = 1952, n.iter=50)
}
#> Loading required package: psychTools
#> Warning: there is no package called ‘psychTools’
#print the path values
mod.k2
#>
#> Mediation/Moderation Analysis
#> Call: mediate(y = OccupAsp ~ Intelligence + Siblings + FatherEd + FatherOcc +
#> (Grades) + (EducExp), data = R.kerch, n.obs = 767, n.iter = 50)
#>
#> The DV (Y) was OccupAsp . The IV (X) was Intelligence Siblings FatherEd FatherOcc . The mediating variable(s) = Grades EducExp .
#>
#> Total effect(c) of Intelligence on OccupAsp = 0.25 S.E. = 0.03 t = 7.29 df= 762 with p = 7.6e-13
#> Direct effect (c') of Intelligence on OccupAsp removing Grades EducExp = -0.04 S.E. = 0.03 t = -1.16 df= 760 with p = 0.25
#> Indirect effect (ab) of Intelligence on OccupAsp through Grades EducExp = 0.29
#> Mean bootstrapped indirect effect = 0.32 with standard error = 0.03 Lower CI = 0.27 Upper CI = 0.37
#>
#> Total effect(c) of Siblings on OccupAsp = -0.09 S.E. = 0.03 t = -2.78 df= 762 with p = 0.0056
#> Direct effect (c') of Siblings on OccupAsp removing Grades EducExp = -0.02 S.E. = 0.03 t = -0.68 df= 760 with p = 0.5
#> Indirect effect (ab) of Siblings on OccupAsp through Grades EducExp = -0.07
#> Mean bootstrapped indirect effect = -0.07 with standard error = 0.02 Lower CI = -0.1 Upper CI = -0.04
#>
#> Total effect(c) of FatherEd on OccupAsp = 0.1 S.E. = 0.04 t = 2.36 df= 762 with p = 0.018
#> Direct effect (c') of FatherEd on OccupAsp removing Grades EducExp = -0.04 S.E. = 0.04 t = -1.16 df= 760 with p = 0.25
#> Indirect effect (ab) of FatherEd on OccupAsp through Grades EducExp = 0.14
#> Mean bootstrapped indirect effect = 0.13 with standard error = 0.02 Lower CI = 0.09 Upper CI = 0.19
#>
#> Total effect(c) of FatherOcc on OccupAsp = 0.2 S.E. = 0.04 t = 4.8 df= 762 with p = 1.9e-06
#> Direct effect (c') of FatherOcc on OccupAsp removing Grades EducExp = 0.1 S.E. = 0.03 t = 2.85 df= 760 with p = 0.0044
#> Indirect effect (ab) of FatherOcc on OccupAsp through Grades EducExp = 0.1
#> Mean bootstrapped indirect effect = 0.11 with standard error = 0.03 Lower CI = 0.06 Upper CI = 0.15
#> R = 0.67 R2 = 0.44 F = 100.9 on 6 and 760 DF p-value: 4.88e-104
#>
#> To see the longer output, specify short = FALSE in the print statement or ask for the summary
#Several interesting test cases are taken from analyses of the Spengler data set
#This is temporarily added to psych from psychTools to help build for CRAN
#Although the sample sizes are actually very large in the first wave, I use the
#sample sizes from the last wave
#We set the n.iter to be 50 instead of the default value of 5,000
if(require("psychTools")) {
mod1 <- mediate(Income.50 ~ IQ + Parental+ (Ed.11) ,data=Spengler,
n.obs = 1952, n.iter=50)
mod2 <- mediate(Income.50 ~ IQ + Parental+ (Ed.11) + (Income.11)
,data=Spengler,n.obs = 1952, n.iter=50)
#Now, compare these models
anova(mod1,mod2)
#Current version does not support two DVs
#mod22 <- mediate(Income.50 + Educ.50 ~ IQ + Parental+ (Ed.11) + (Income.11)
# ,data=Spengler,n.obs = 1952, n.iter=50)
}
#> Loading required package: psychTools
#> Warning: there is no package called ‘psychTools’