Score items using regression or correlation based weights

Item weights from bestScales or lmCor are used to find weighted scale scores. In contrast to the unit weights used in scoreItems, scoreWtd will multiply the data by a set of weights to find scale scores. These weight may come from a regression (e.g., lm or lmCor) or may be the zero order correlation weights from bestScales.

scoreWtd(weights, items, std = TRUE, sums = FALSE, impute = "none")

Arguments

weights

This is just a matrix of weights to use for each item for each scale.

items

Matrix or dataframe of raw item scores

std

if TRUE, then find weighted standard scores else just use raw data

sums

By default, find the average item score. If sums = TRUE, then find the sum scores. This is useful for regression with an intercept term

impute

impute="median" replaces missing values with the item medians, impute = "mean" replaces values with the mean response. impute="none" the subject's scores are based upon the average of the keyed, but non missing scores. impute = "none" is probably more appropriate for a large number of missing cases (e.g., SAPA data).

Details

Although meant for finding correlation weighted scores using the weights from bestScales, it also possible to use alternative weight matrices, such as those returned by the coefficients in lm.

Value

A data frame of scores.

Author

William Revelle

See also

bestScales and lmCor

Examples

  
#find the weights from a regression model and then apply them to a new set
#derivation of weights from the first 20 cases 
model.lm <- lm(rating ~ complaints + privileges + learning,data=attitude[1:20,])
#or use lmCor to find the coefficents
model <- lmCor(rating ~ complaints + privileges +learning,data=attitude[1:20,],std=FALSE)

 
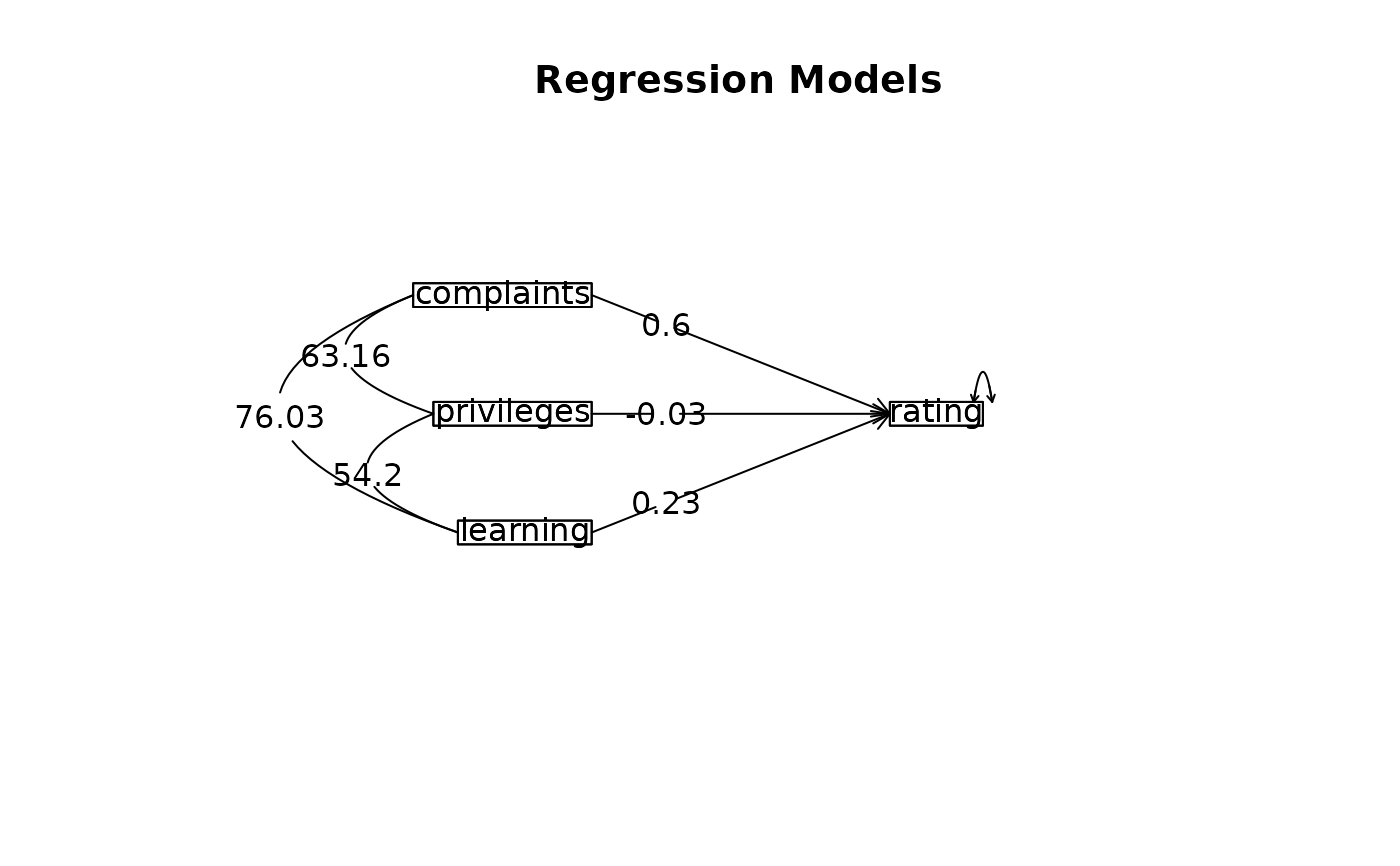 #Apply these to a different set of data (the last 10 cases)
  #note that the regression coefficients need to be a matrix
  scores.lm <- scoreWtd(as.matrix(model.lm$coefficients),attitude[21:30,],sums=TRUE,std=FALSE)
scores <- scoreWtd(model$coefficients,attitude[21:30,],sums=TRUE,std=FALSE)
describe(scores)  
#>    vars  n  mean    sd median trimmed   mad   min   max range  skew kurtosis
#> X1    1 10 62.79 11.84  62.68   63.16 14.86 44.19 78.39  34.2 -0.18    -1.58
#>      se
#> X1 3.74