Remove Columns (or Rows) From a Matrix to Make It Full Rank

From the QR decomposition with pivoting, (qr(x, tol) if \(n \ge p\)), if the matrix is not of full rank, the corresponding columns (\(n \ge p\)) or rows (\(n < p\)) are omitted to form a full rank matrix.

<!-- % -&gt; ../R/adjoutlyingness.R -->
fullRank(x, tol = 1e-7, qrx = qr(x, tol=tol))

Arguments

x

a numeric matrix of dimension \(n \times p\), or a similar object for which qr() works.

tol

tolerance for determining rank (deficiency). Currently is simply passed to qr.

qrx

optionally may be used to pass a qr(x, ..); only used when p <= n.

Value

a version of the matrix x, with less columns or rows if x's rank was smaller than min(n,p).

If x is of full rank, it is returned unchanged.

Author

Martin Maechler

Note

This is useful for robustness algorithms that rely on \(X\) matrices of full rank, e.g., adjOutlyingness.

This also works for numeric data frames and whenever qr() works correctly.

See also

qr; for more sophisticated rank determination, rankMatrix from package Matrix.

Examples

stopifnot(identical(fullRank(wood), wood))

## More sophisticated and delicate
dim(T <- tcrossprod(data.matrix(toxicity))) # 38 x 38
#> [1] 38 38
dim(T. <- fullRank(T)) # 38 x 10
#> [1] 38 10
if(requireNamespace("Matrix")) {
  rMmeths <- eval(formals(Matrix::rankMatrix)$method)
  rT. <- sapply(rMmeths, function(.m.) Matrix::rankMatrix(T., method = .m.))
  print(rT.) # "qr" (= "qrLinpack"): 13,  others rather 10
}
#> Loading required namespace: Matrix
#>  tolNorm2      qr.R qrLINPACK        qr   useGrad maybeGrad 
#>        10        10        10        10         9        10 
dim(T.2 <- fullRank(T, tol = 1e-15))# 38 x 18
#> [1] 38 16
dim(T.3 <- fullRank(T, tol = 1e-12))# 38 x 13
#> [1] 38 10
dim(T.3 <- fullRank(T, tol = 1e-10))# 38 x 13
#> [1] 38 10
dim(T.3 <- fullRank(T, tol = 1e-8 ))# 38 x 12
#> [1] 38 10
dim(T.) # default from above          38 x 10
#> [1] 38 10
dim(T.3 <- fullRank(T, tol = 1e-5 ))# 38 x 10 -- still
#> [1] 38 10

plot(svd(T, 0,0)$d, log="y", main = "singular values of T", yaxt="n")
axis(2, at=10^(-14:5), las=1)

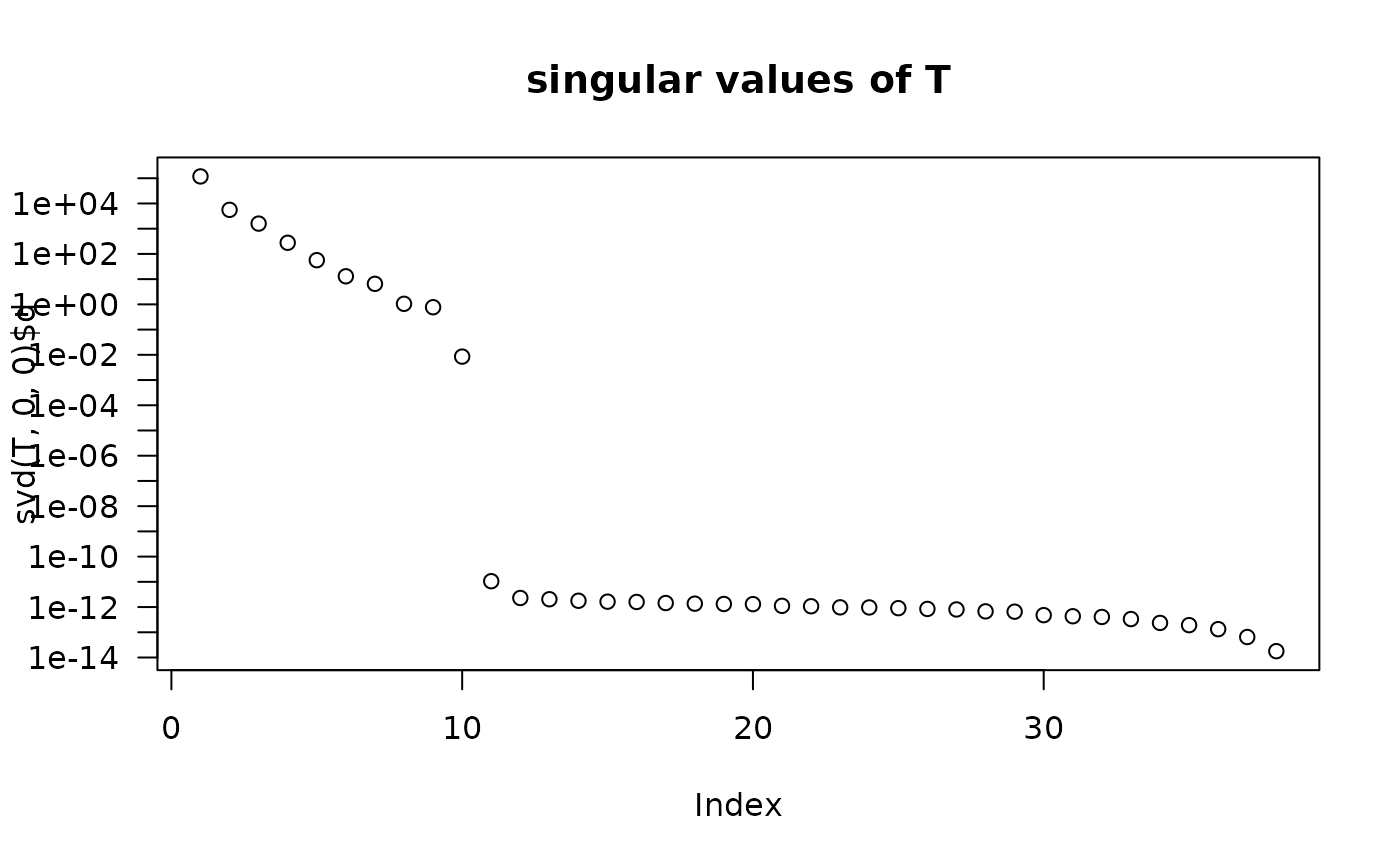## pretty clearly indicates that  rank 10  is "correct" here.