Compute (Skewness-adjusted) Multivariate Outlyingness

For an \(n \times p\) data matrix (or data frame) x, compute the “outlyingness” of all \(n\) observations. Outlyingness here is a generalization of the Donoho-Stahel outlyingness measure, where skewness is taken into account via the medcouple, mc().

adjOutlyingness(x, ndir = 250, p.samp = p, clower = 4, cupper = 3,
                IQRtype = 7,
                alpha.cutoff = 0.75, coef = 1.5,
                qr.tol = 1e-12, keep.tol = 1e-12,
                only.outlyingness = FALSE, maxit.mult = max(100, p),
                trace.lev = 0,
                mcReflect = n <= 100, mcScale = TRUE, mcMaxit = 2*maxit.mult,
                mcEps1 = 1e-12, mcEps2 = 1e-15,
                mcTrace = max(0, trace.lev-1))

Arguments

x: a numeric \(n \times p\) matrix or data.frame, which must be of full rank \(p\).
ndir: positive integer specifying the number of directions that should be searched.
p.samp: the sample size to use for finding good random directions, must be at least p. The default, p had been hard coded previously.
clower, cupper: the constant to be used for the lower and upper tails, in order to transform the data towards symmetry. You can set clower = 0, cupper = 0 to get the non-adjusted, i.e., classical (“central” or “symmetric”) outlyingness. In that case, mc() is not used.
IQRtype: a number from 1:9, denoting type of empirical quantile computation for the IQR(). The default 7 corresponds to quantile's and IQR's default. MM has evidence that type=6 would be a bit more stable for small sample size.
alpha.cutoff: number in (0,1) specifying the quantiles \((\alpha, 1-\alpha)\) which determine the “outlier” cutoff. The default, using quartiles, corresponds to the definition of the medcouple (mc), but there is no stringent reason for using the same alpha for the outlier cutoff.
coef: positive number specifying the factor with which the interquartile range (IQR) is multiplied to determine ‘boxplot hinges’-like upper and lower bounds.
qr.tol: positive tolerance to be used for qr and solve.qr for determining the ndir directions, each determined by a random sample of \(p\) (out of \(n\)) observations. Note that the default \(10^{-12}\) is rather small, and qr's default = 1e-7 may be more appropriate.
keep.tol: positive tolerance to determine which of the sample direction should be kept, namely only those for which \(\|x\| \cdot \|B\|\) is larger than keep.tol.
only.outlyingness: logical indicating if the final outlier determination should be skipped. In that case, a vector is returned, see ‘Value:’ below.
maxit.mult: integer factor; maxit <- maxit.mult * ndir will determine the maximal number of direction searching iterations. May need to be increased for higher dimensional data, though increasing ndir may be more important.
trace.lev: an integer, if positive allows to monitor the direction search.

mcReflect: passed as doReflect to mc().
mcScale: passed as doScale to mc().
mcMaxit: passed as maxit to mc().
mcEps1: passed as eps1 to mc(); the default is slightly looser (100 larger) than the default for mc().
mcEps2: passed as eps2 to mc().
mcTrace: passed as trace.lev to mc().

Note

If there are too many degrees of freedom for the projections, i.e., when \(n \le 4p\), the current definition of adjusted outlyingness is ill-posed, as one of the projections may lead to a denominator (quartile difference) of zero, and hence formally an adjusted outlyingness of infinity. The current implementation avoids Inf results, but will return seemingly random adjout values of around \(10^{14} -- 10^{15}\) which may be completely misleading, see, e.g., the longley data example.

The result is random as it depends on the sample of ndir directions chosen; specifically, to get sub samples the algorithm uses sample.int(n, p.samp) which from R version 3.6.0 depends on RNGkind(*, sample.kind). Exact reproducibility of results from R versions 3.5.3 and earlier, requires setting RNGversion("3.5.0"). In any case, do use set.seed() yourself for reproducibility!

Till Aug/Oct. 2014, the default values for clower and cupper were accidentally reversed, and the signs inside exp(.) where swapped in the (now corrected) two expressions


 tup <- Q3 + coef * IQR * exp(.... + clower * tmc * (tmc < 0))
 tlo <- Q1 - coef * IQR * exp(.... - cupper * tmc * (tmc < 0))

already in the code from Antwerpen (mcrsoft/adjoutlingness.R), contrary to the published reference.

Further, the original algorithm had not been scale-equivariant in the direction construction, which has been amended in 2014-10 as well.

The results, including diagnosed outliers, therefore have changed, typically slightly, since robustbase version 0.92-0.

Details

FIXME: Details in the comment of the Matlab code; also in the reference(s).

The method as described can be useful as preprocessing in FASTICA (http://research.ics.aalto.fi/ica/fastica/ see also the R package fastICA.

Value

If only.outlyingness is true, a vector adjout, otherwise, as by default, a list with components

adjout: numeric of length(n) giving the adjusted outlyingness of each observation.
cutoff: cutoff for “outlier” with respect to the adjusted outlyingnesses, and depending on alpha.cutoff.
nonOut: logical of length(n), TRUE when the corresponding observation is non-outlying with respect to the cutoff and the adjusted outlyingnesses.

References

Brys, G., Hubert, M., and Rousseeuw, P.J. (2005) A Robustification of Independent Component Analysis; Journal of Chemometrics, 19, 1–12.

Hubert, M., Van der Veeken, S. (2008) Outlier detection for skewed data; Journal of Chemometrics 22, 235–246; doi:10.1002/cem.1123 .

For the up-to-date reference, please consult https://wis.kuleuven.be/statdatascience/robust

Author

Guy Brys; help page and improvements by Martin Maechler

Examples

## An Example with bad condition number and "border case" outliers

dim(longley) # 16 x 7  // set seed, as result is random :
#> [1] 16  7
set.seed(31)
ao1 <- adjOutlyingness(longley, mcScale=FALSE)
## which are outlying ?
which(!ao1$nonOut) ## for this seed, two: "1956", "1957"; (often: none)
#> named integer(0)
## For seeds 1:100, we observe (Linux 64b)
if(FALSE) {
  adjO <- sapply(1:100, function(iSeed) {
            set.seed(iSeed); adjOutlyingness(longley)$nonOut })
  table(nrow(longley) - colSums(adjO))
}
## #{outl.}:  0  1  2  3
## #{cases}: 74 17  6  3


## An Example with outliers :

dim(hbk)
#> [1] 75  4
set.seed(1)
ao.hbk <- adjOutlyingness(hbk)
str(ao.hbk)
#> List of 7
#>  $ adjout      : num [1:75] 34.3 35.3 37.3 37.9 37.5 ...
#>  $ iter        : int 250
#>  $ ndir.final  : int 250
#>  $ MCadjout    : num 0.257
#>  $ Qalph.adjout: Named num [1:2] 1.42 2.63
#>   ..- attr(*, "names")= chr [1:2] "25%" "75%"
#>  $ cutoff      : Named num 6.55
#>   ..- attr(*, "names")= chr "75%"
#>  $ nonOut      : logi [1:75] FALSE FALSE FALSE FALSE FALSE FALSE ...
hist(ao.hbk $adjout)## really two groups

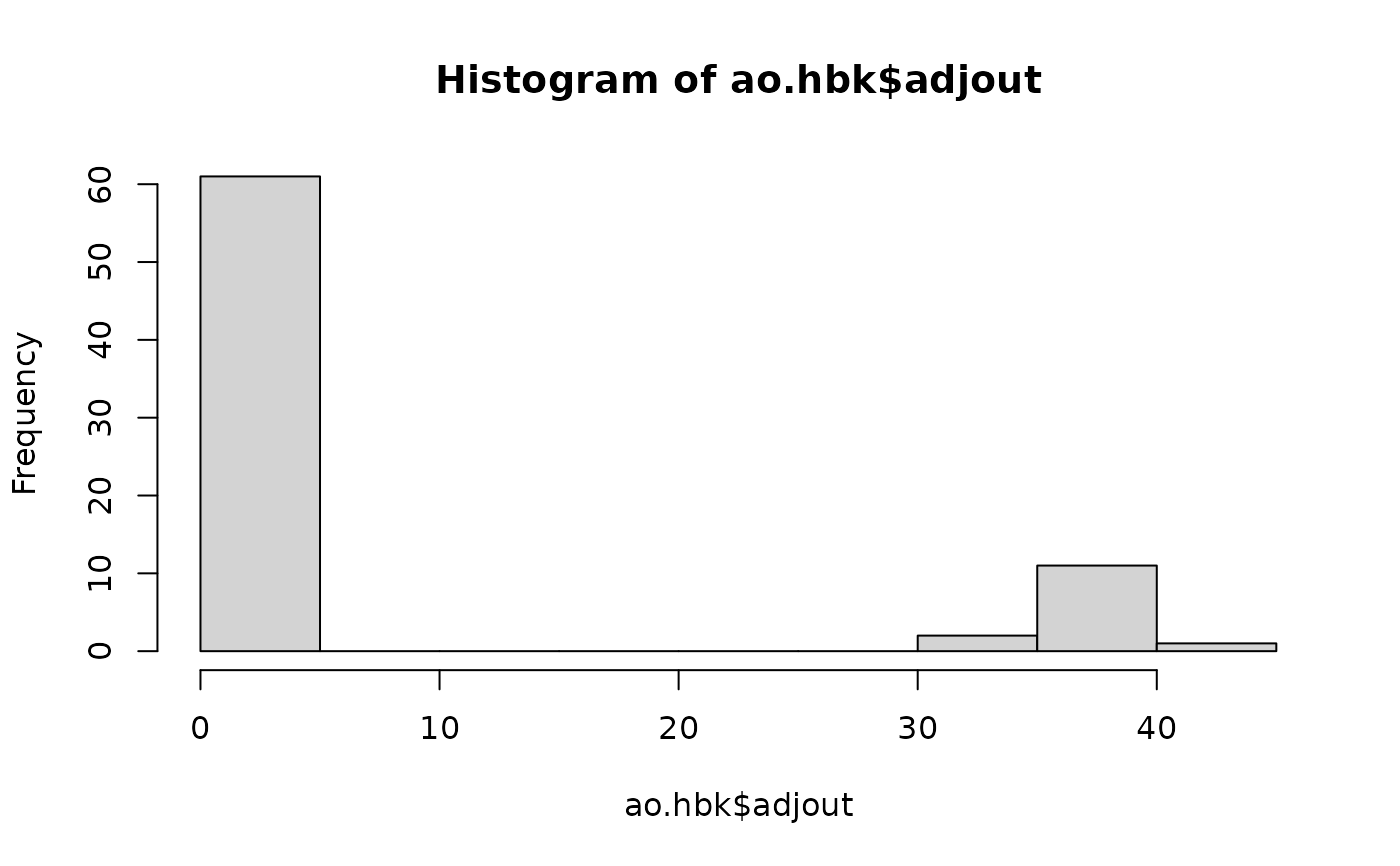table(ao.hbk$nonOut)## 14 outliers, 61 non-outliers:
#> 
#> FALSE  TRUE 
#>    14    61 
## outliers are :
which(! ao.hbk$nonOut) # 1 .. 14   --- but not for all random seeds!
#>  [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14

## here, they are(*) the same as found by (much faster) MCD:
## *) only "almost", since the 2023-05 change to covMcd() 
cc <- covMcd(hbk)
table(cc = cc$mcd.wt, ao = ao.hbk$nonOut)# one differ..:
#>    ao
#> cc  FALSE TRUE
#>   0    14    1
#>   1     0   60
stopifnot(sum(cc$mcd.wt != ao.hbk$nonOut) <= 1)

## This is revealing: About 1--2 cases, where outliers are *not* == 1:14
## (2023: ~ 1/8 [sec] per call)
if(interactive()) {
  for(i in 1:30) {
    print(system.time(ao.hbk <- adjOutlyingness(hbk)))
    if(!identical(iout <- which(!ao.hbk$nonOut), 1:14)) {
   cat("Outliers:\n"); print(iout)
    }
  }
}

## "Central" outlyingness: *not* calling mc()  anymore, since 2014-12-11:
trace(mc)
out <- capture.output(
  oo <- adjOutlyingness(hbk, clower=0, cupper=0)
)
untrace(mc)
stopifnot(length(out) == 0)

## A rank-deficient case
T <- tcrossprod(data.matrix(toxicity))
try(adjOutlyingness(T, maxit. = 20, trace.lev = 2)) # fails and recommends:
#>  it=1000: rank(qr(P ..)) = 10 < p = 38
#>  it=2000: rank(qr(P ..)) = 10 < p = 38
#>  it=3000: rank(qr(P ..)) = 10 < p = 38
#>  it=4000: rank(qr(P ..)) = 10 < p = 38
#> Error in adjOutlyingness(T, maxit. = 20, trace.lev = 2) : 
#>   Matrix 'x' is not of full rank: rankM(x) = 10 < p = 38
#>  Use fullRank(x) instead
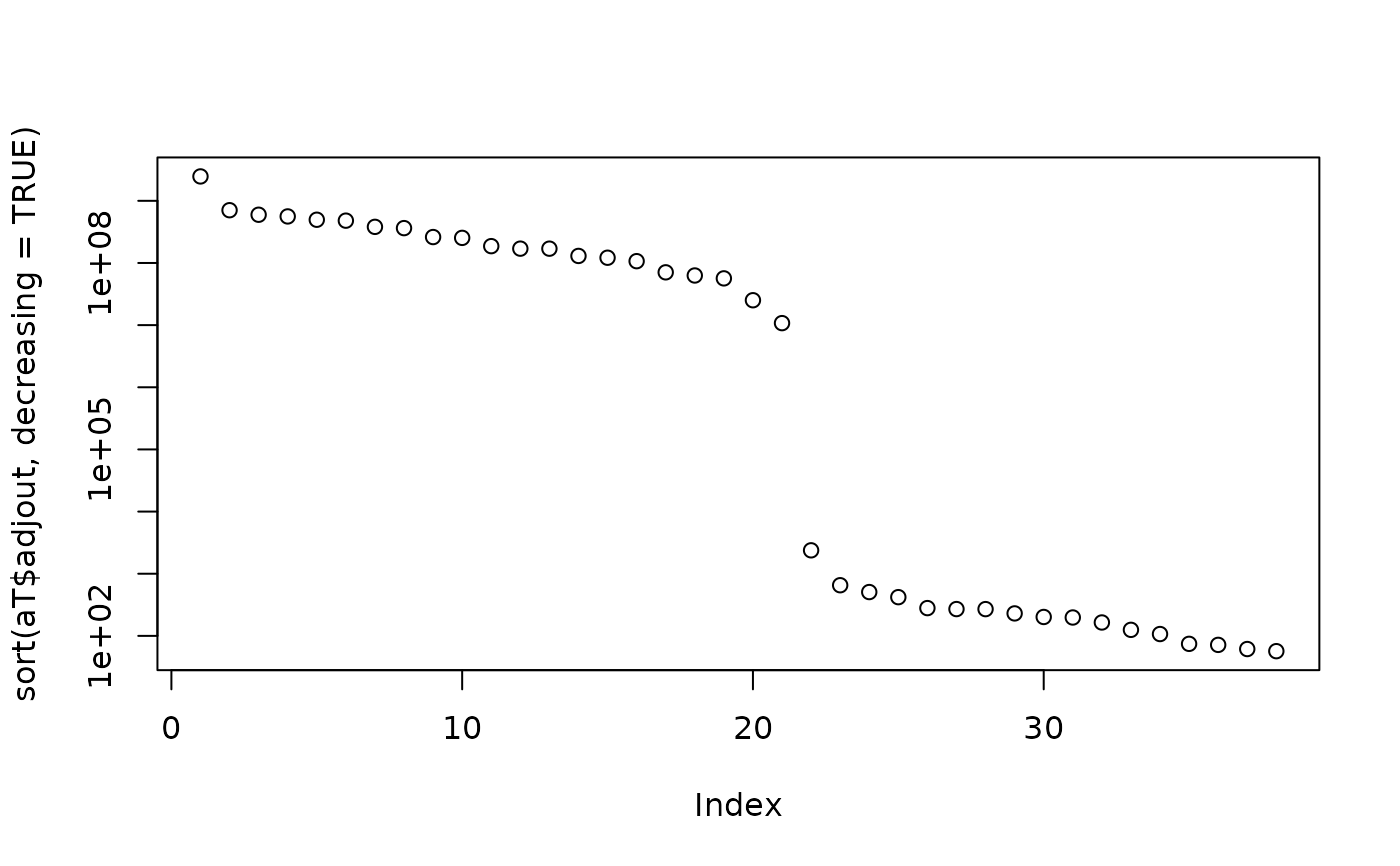
T. <- fullRank(T)
aT <- adjOutlyingness(T.)
plot(sort(aT$adjout, decreasing=TRUE), log="y")

plot(T.[,9:10], col = (1:2)[1 + (aT$adjout > 10000)])

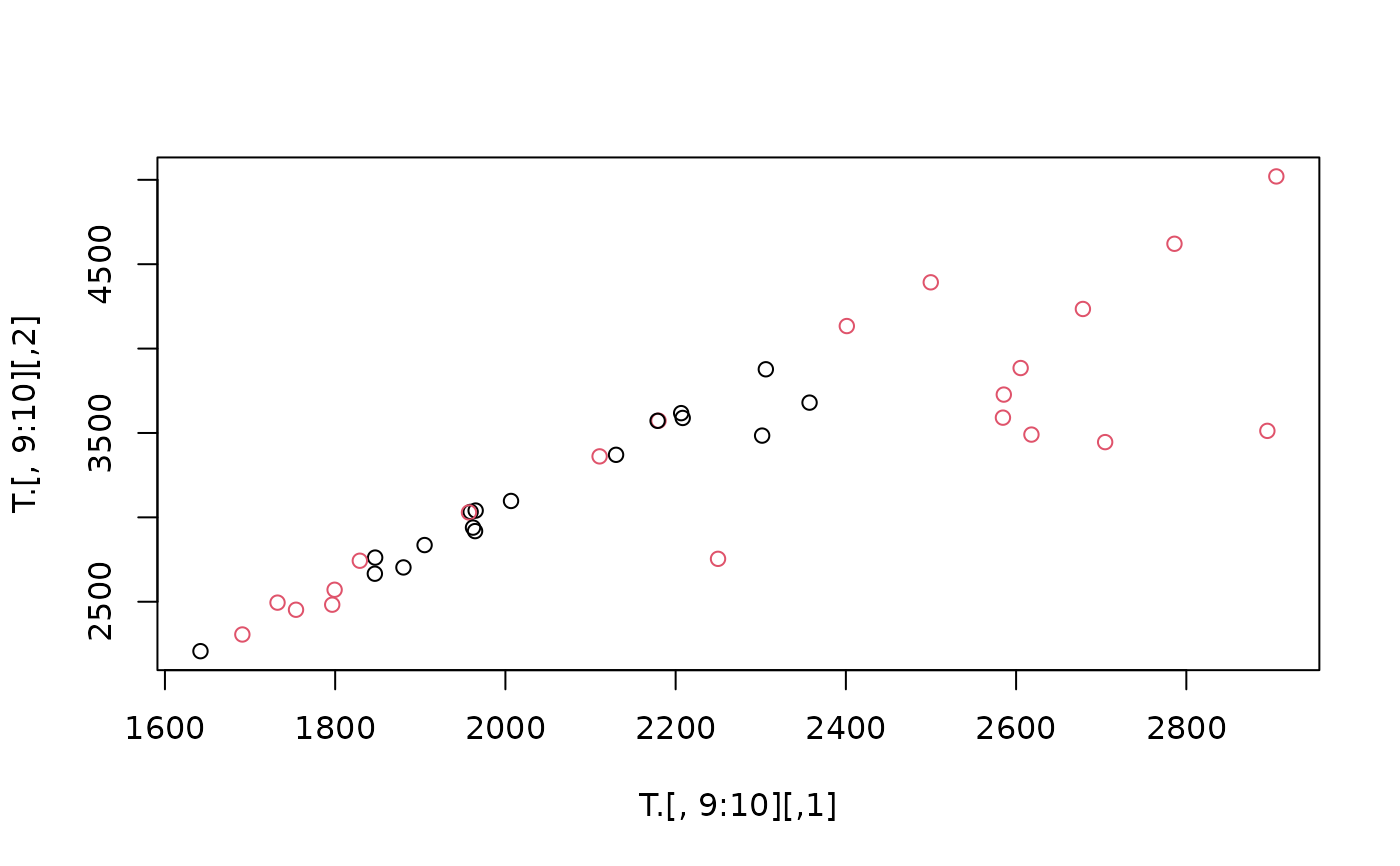## .. (not conclusive; directions are random, more 'ndir' makes a difference!)