Robust Fitting of Nonlinear Regression Models
nlrob.Rdnlrob fits a nonlinear regression model by robust methods.
Per default, by an M-estimator, using iterated reweighted least
squares (called “IRLS” or also “IWLS”).
nlrob(formula, data, start, lower, upper,
weights = NULL, na.action = na.fail,
method = c("M", "MM", "tau", "CM", "mtl"),
psi = .Mwgt.psi1("huber", cc=1.345), scale = NULL,
test.vec = c("resid", "coef", "w"), maxit = 20,
tol = 1e-06, acc, algorithm = "default", doCov = FALSE, model = FALSE,
control = if(method == "M") nls.control() else
nlrob.control(method, optArgs = list(trace=trace), ...),
trace = FALSE, ...)
# S3 method for class 'nlrob'
fitted(object, ...)
# S3 method for class 'nlrob'
residuals(object, type = , ...)<!-- % FIXME: more 'type's + DOCU -->
# S3 method for class 'nlrob'
predict(object, newdata, ...)Arguments
- formula
a nonlinear
formulaincluding variables and parameters of the model, such asy ~ f(x, theta)(cf.nls). (For some checks: if \(f(.)\) is linear, then we need parentheses, e.g.,y ~ (a + b * x); (note that._nlrob.wis not allowed as variable or parameter name))- data
an optional data frame containing the variables in the model. If not found in
data, the variables are taken fromenvironment(formula), typically the environment from whichnlrobis called.- start
a named numeric vector of starting parameters estimates, only for
method = "M".- lower, upper
numeric vectors of lower and upper bounds; if needed, will be replicated to be as long as the longest of
start,lowerorupper. For (the default)method = "M", if the bounds are unspecified all parameters are assumed to be unconstrained; also, for method"M", bounds can only be used with the"port"algorithm. They are ignored, with a warning, in cases they have no effect.For all other methods, currently these bounds must be specified as finite values, and one of them must have
namesmatching the parameter names informula.For methods
"CM"and"mtl", the bounds must additionally have an entry named"sigma"as that is determined simultaneously in the same optimization, and hence itslowerbound must not be negative.- weights
an optional vector of weights to be used in the fitting process (for intrinsic weights, not the weights
wused in the iterative (robust) fit). I.e.,sum(w * e^2)is minimized withe= residuals, \(e_i = y_i - f(xreg_i, \theta)\), where \(f(x,\theta)\) is the nonlinear function, andware the robust weights fromresid * weights.- na.action
a function which indicates what should happen when the data contain
NAs. The default action is for the procedure to fail. If NAs are present, usena.excludeto have residuals withlength == nrow(data) == length(w), whereware the weights used in the iterative robust loop. This is better if the explanatory variables informulaare time series (and so the NA location is important). For this reason,na.omit, which leads to omission of cases with missing values on any required variable, is not suitable here since the residuals length is different fromnrow(data) == length(w).- method
a character string specifying which method to use. The default is
"M", for historical and back-compatibility reasons. For the other methods, primarily seenlrob.algorithms.- "M"
Computes an M-estimator, using
nls(*, weights=*)iteratively (hence, IRLS) with weights equal to \(\psi(r_i) / r_i\), where \(r_i\) is the i-the residual from the previous fit.- "MM"
Computes an MM-estimator, starting from
init, either "S" or "lts".
% more: FIXME
- "tau"
Computes a Tau-estimator.
- "CM"
Computes a “Constrained M” (=: CM) estimator.
- "mtl"
Compute as “Maximum Trimmed Likelihood” (=: MTL) estimator.
Note that all methods but
"M"are “random”, hence typically to be preceded byset.seed()in usage, see alsonlrob.algorithms.- psi
a function (possibly by name) of the form
g(x, 'tuning constant(s)', deriv)that forderiv=0returns \(\psi(x)/x\) and forderiv=1returns \(\psi'(x)\). Note that tuning constants can not be passed separately, but directly via the specification ofpsi, typically via a simple.Mwgt.psi1()call as per default.Note that this has been a deliberately non-backcompatible change for robustbase version 0.90-0 (summer 2013 – early 2014).
- scale
when not
NULL(default), a positive number specifying a scale kept fixed during the iterations (and returned asScalecomponent).- test.vec
character string specifying the convergence criterion. The relative change is tested for residuals with a value of
"resid"(the default), for coefficients with"coef", and for weights with"w".- maxit
maximum number of iterations in the robust loop.
- tol
non-negative convergence tolerance for the robust fit.
- acc
previous name for
tol, now deprecated.- algorithm
character string specifying the algorithm to use for
nls, see there, only whenmethod = "M". The default algorithm is a Gauss-Newton algorithm.- doCov
a logical specifying if
nlrob()should compute the asymptotic variance-covariance matrix (seevcov) already. This used to be hard-wired toTRUE; however, the default has been set toFALSE, asvcov(obj)andsummary(obj)can easily compute it when needed.- model
a
logicalindicating if themodel.frameshould be returned as well.- control
an optional list of control settings.
- for
method = "M": settings for
nls(). Seenls.controlfor the names of the settable control values and their effect.- for all
methods but"M": a list, typically resulting from
nlrob.control(method, *).
- for
- trace
logical value indicating if a “trace” of the
nlsiteration progress should be printed. Default isFALSE.
IfTRUE, in each robust iteration, the residual sum-of-squares and the parameter values are printed at the conclusion of eachnlsiteration. When the"plinear"algorithm is used, the conditional estimates of the linear parameters are printed after the nonlinear parameters.- object
an R object of class
"nlrob", typically resulting fromnlrob(..).- ...
for
nlrob: only whenmethodis not"M", optional arguments fornlrob.control;
for other functions: potentially optional arguments passed to the extractor methods.- type
a string specifying the type of residuals desired. Currently,
"response"and"working"are supported.- newdata
a data frame (or list) with the same names as the original
data, see e.g.,predict.nls.
Details
For method = "M", iterated reweighted least squares
(“IRLS” or “IWLS”) is used, calling nls(*,
weights= .) where weights \(w_i\) are proportional to
\(\psi(r_i/ \hat{\sigma})\).
All other methods minimize differently, and work without
nls. See nlrob.algorithms
for details.
Value
nlrob() returns an object of S3 class "nlrob",
for method = "M" also inheriting from class "nls", (see
nls).
It is a list with several components; they are not documented yet,
as some of them will probably change.
Instead, rather use “accessor” methods, where possible:
There are methods (at least) for the generic accessor functions
summary(), coefficients() (aka coef())
fitted.values(), residuals(), sigma() and
vcov(), the latter for the variance-covariance matrix of
the estimated parameters, as returned by coef(), i.e., not
including the variance of the errors.
For nlrob() results, estimethod() returns the
“estimation method”, which coincides with the method
argument used.
residuals(.), by default type = "response", returns
the residuals \(e_i\), defined above as
\(e_i = Y_i - f_(x_i, \hat\theta)\).
These differ from the standardized or weighted residuals which, e.g.,
are assumed to be normally distributed, and a version of which is
returned in working.residuals component.
Note
This function (with the only method "M") used to be named
rnls and has been in package sfsmisc in the past, but
been dropped there.
Examples
DNase1 <- DNase[ DNase$Run == 1, ]
## note that selfstarting models don't work yet % <<< FIXME !!!
##--- without conditional linearity ---
## classical
fmNase1 <- nls( density ~ Asym/(1 + exp(( xmid - log(conc) )/scal ) ),
data = DNase1,
start = list( Asym = 3, xmid = 0, scal = 1 ),
trace = TRUE )
#> 14.32279 (3.02e+01): par = (3 0 1)
#> 0.4542698 (9.73e+00): par = (2.115246 0.8410193 1.200064)
#> 0.05869603 (3.34e+00): par = (2.446376 1.747516 1.189515)
#> 0.005663524 (4.26e-01): par = (2.294087 1.412198 1.020463)
#> 0.004791528 (2.02e-02): par = (2.341429 1.479688 1.040758)
#> 0.004789569 (1.65e-04): par = (2.345135 1.483047 1.041439)
#> 0.004789569 (1.96e-06): par = (2.345179 1.483089 1.041454)
summary( fmNase1 )
#>
#> Formula: density ~ Asym/(1 + exp((xmid - log(conc))/scal))
#>
#> Parameters:
#> Estimate Std. Error t value Pr(>|t|)
#> Asym 2.34518 0.07815 30.01 2.17e-13 ***
#> xmid 1.48309 0.08135 18.23 1.22e-10 ***
#> scal 1.04145 0.03227 32.27 8.51e-14 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> Residual standard error: 0.01919 on 13 degrees of freedom
#>
#> Number of iterations to convergence: 6
#> Achieved convergence tolerance: 1.957e-06
#>
## robust
RmN1 <- nlrob( density ~ Asym/(1 + exp(( xmid - log(conc) )/scal ) ),
data = DNase1, trace = TRUE,
start = list( Asym = 3, xmid = 0, scal = 1 ))
#> robust iteration 1
#> 14.32279 (3.02e+01): par = (3 0 1)
#> 0.4542698 (9.73e+00): par = (2.115246 0.8410193 1.200064)
#> 0.05869603 (3.34e+00): par = (2.446376 1.747516 1.189515)
#> 0.005663524 (4.26e-01): par = (2.294087 1.412198 1.020463)
#> 0.004791528 (2.02e-02): par = (2.341429 1.479688 1.040758)
#> 0.004789569 (1.65e-04): par = (2.345135 1.483047 1.041439)
#> 0.004789569 (1.96e-06): par = (2.345179 1.483089 1.041454)
#> --> irls.delta(previous, resid) = 0.999803 -- *not* converged
#> robust iteration 2
#> 0.003971483 (6.54e-02): par = (2.345179 1.483089 1.041454)
#> 0.003954569 (1.07e-03): par = (2.356445 1.495544 1.043788)
#> 0.003954565 (2.77e-06): par = (2.356586 1.49565 1.043815)
#> --> irls.delta(previous, resid) = 0.0614628 -- *not* converged
#> robust iteration 3
#> 0.003934724 (1.25e-02): par = (2.356586 1.49565 1.043815)
#> 0.003934110 (8.81e-05): par = (2.358633 1.498205 1.044647)
#> 0.003934110 (7.21e-07): par = (2.358657 1.498229 1.044655)
#> --> irls.delta(previous, resid) = 0.0121516 -- *not* converged
#> robust iteration 4
#> 0.003930685 (4.06e-03): par = (2.358657 1.498229 1.044655)
#> 0.003930620 (2.54e-05): par = (2.359307 1.499046 1.044928)
#> 0.003930620 (2.46e-07): par = (2.359314 1.499053 1.044931)
#> --> irls.delta(previous, resid) = 0.00395056 -- *not* converged
#> robust iteration 5
#> 0.003929580 (1.33e-03): par = (2.359314 1.499053 1.044931)
#> 0.003929573 (8.00e-06): par = (2.359525 1.49932 1.04502)
#> --> irls.delta(previous, resid) = 0.00128457 -- *not* converged
#> robust iteration 6
#> 0.003929244 (4.36e-04): par = (2.359525 1.49932 1.04502)
#> 0.003929244 (2.70e-06): par = (2.359596 1.499409 1.04505)
#> --> irls.delta(previous, resid) = 0.000422963 -- *not* converged
#> robust iteration 7
#> 0.003929132 (1.44e-04): par = (2.359596 1.499409 1.04505)
#> 0.003929132 (8.42e-07): par = (2.35962 1.499438 1.04506)
#> --> irls.delta(previous, resid) = 0.000139343 -- *not* converged
#> robust iteration 8
#> 0.003929095 (4.73e-05): par = (2.35962 1.499438 1.04506)
#> 0.003929095 (3.57e-07): par = (2.359628 1.499448 1.045063)
#> --> irls.delta(previous, resid) = 4.58756e-05 -- *not* converged
#> robust iteration 9
#> 0.003929083 (1.56e-05): par = (2.359628 1.499448 1.045063)
#> 0.003929083 (4.07e-08): par = (2.35963 1.499451 1.045064)
#> --> irls.delta(previous, resid) = 1.5156e-05 -- *not* converged
#> robust iteration 10
#> 0.003929079 (5.11e-06): par = (2.35963 1.499451 1.045064)
summary( RmN1 )
#>
#> Call:
#> nlrob(formula = density ~ Asym/(1 + exp((xmid - log(conc))/scal)),
#> data = DNase1, start = list(Asym = 3, xmid = 0, scal = 1),
#> trace = TRUE, algorithm = "default")
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.0322811 -0.0130976 -0.0008932 0.0095784 0.0404174
#>
#> Parameters:
#> Estimate Std. Error t value Pr(>|t|)
#> Asym 2.35963 0.08627 27.35 7.10e-13 ***
#> xmid 1.49945 0.09022 16.62 3.87e-10 ***
#> scal 1.04506 0.03504 29.83 2.34e-13 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> Robust residual standard error: 0.01829
#> Convergence in 10 IRWLS iterations
#>
#> Robustness weights:
#> 14 weights are ~= 1. The remaining 2 ones are
#> 11 13
#> 0.6087 0.7621
##--- using conditional linearity ---
## classical
fm2DNase1 <- nls( density ~ 1/(1 + exp(( xmid - log(conc) )/scal ) ),
data = DNase1,
start = c( xmid = 0, scal = 1 ),
alg = "plinear", trace = TRUE )
#> 0.7139315 (5.02e+00): par = (0 1 1.453853)
#> 0.1445295 (4.63e+00): par = (1.640243 1.390186 2.461754)
#> 0.008302151 (1.76e+00): par = (1.620899 1.054228 2.478388)
#> 0.004794192 (5.08e-02): par = (1.485226 1.043709 2.347334)
#> 0.004789569 (1.58e-04): par = (1.48313 1.041468 2.345218)
#> 0.004789569 (1.10e-06): par = (1.48309 1.041455 2.34518)
summary( fm2DNase1 )
#>
#> Formula: density ~ 1/(1 + exp((xmid - log(conc))/scal))
#>
#> Parameters:
#> Estimate Std. Error t value Pr(>|t|)
#> xmid 1.48309 0.08135 18.23 1.22e-10 ***
#> scal 1.04145 0.03227 32.27 8.51e-14 ***
#> .lin 2.34518 0.07815 30.01 2.17e-13 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> Residual standard error: 0.01919 on 13 degrees of freedom
#>
#> Number of iterations to convergence: 5
#> Achieved convergence tolerance: 1.102e-06
#>
## robust
frm2DNase1 <- nlrob(density ~ 1/(1 + exp(( xmid - log(conc) )/scal ) ),
data = DNase1, start = c( xmid = 0, scal = 1 ),
alg = "plinear", trace = TRUE )
#> robust iteration 1
#> 0.3048110 (4.49e+00): par = (0 1 1.211703)
#> 0.07453107 (4.07e+00): par = (1.79994 1.389332 2.444108)
#> 0.005090972 (1.88e+00): par = (1.608012 1.036879 2.499053)
#> 0.002808544 (4.53e-03): par = (1.497344 1.042272 2.358425)
#> 0.002808302 (2.07e-04): par = (1.494768 1.041249 2.355939)
#> 0.002808302 (6.97e-07): par = (1.494782 1.041248 2.355956)
#> --> irls.delta(previous, resid) = 1.00066 -- *not* converged
#> robust iteration 2
#> 0.003921933 (8.09e-02): par = (1.494782 1.041248 2.355292)
#> 0.003912465 (1.20e-04): par = (1.497919 1.044494 2.358442)
#> 0.003912465 (7.23e-07): par = (1.497985 1.044519 2.358504)
#> --> irls.delta(previous, resid) = 0.0468789 -- *not* converged
#> robust iteration 3
#> 0.003930940 (1.41e-03): par = (1.497985 1.044519 2.358321)
#> 0.003930894 (1.70e-05): par = (1.498919 1.044885 2.359206)
#> 0.003930894 (1.14e-07): par = (1.498928 1.044888 2.359214)
#> --> irls.delta(previous, resid) = 0.00529692 -- *not* converged
#> robust iteration 4
#> 0.003929736 (1.34e-03): par = (1.498928 1.044888 2.359162)
#> 0.003929730 (4.31e-06): par = (1.499278 1.045006 2.359492)
#> --> irls.delta(previous, resid) = 0.00169286 -- *not* converged
#> robust iteration 5
#> 0.003929297 (4.48e-04): par = (1.499278 1.045006 2.359475)
#> 0.003929297 (1.28e-06): par = (1.499395 1.045045 2.359585)
#> --> irls.delta(previous, resid) = 0.000557837 -- *not* converged
#> robust iteration 6
#> 0.003929149 (1.48e-04): par = (1.499395 1.045045 2.35958)
#> 0.003929149 (3.88e-07): par = (1.499433 1.045058 2.359616)
#> --> irls.delta(previous, resid) = 0.000183778 -- *not* converged
#> robust iteration 7
#> 0.003929101 (4.87e-05): par = (1.499433 1.045058 2.359614)
#> 0.003929101 (1.39e-07): par = (1.499446 1.045062 2.359626)
#> --> irls.delta(previous, resid) = 6.05132e-05 -- *not* converged
#> robust iteration 8
#> 0.003929085 (1.60e-05): par = (1.499446 1.045062 2.359626)
#> 0.003929085 (5.26e-08): par = (1.49945 1.045064 2.35963)
#> --> irls.delta(previous, resid) = 1.99453e-05 -- *not* converged
#> robust iteration 9
#> 0.003929080 (5.29e-06): par = (1.49945 1.045064 2.359629)
#> --> irls.delta(previous, resid) = 4.31028e-06 -- *not* converged
#> robust iteration 10
#> 0.003929081 (5.86e-06): par = (1.49945 1.045064 2.359629)
summary( frm2DNase1 )
#>
#> Call:
#> nlrob(formula = density ~ 1/(1 + exp((xmid - log(conc))/scal)),
#> data = DNase1, start = c(xmid = 0, scal = 1), algorithm = "plinear",
#> trace = TRUE)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> 0.003927 0.107372 0.280145 0.641955 1.002490
#>
#> Parameters:
#> Estimate Std. Error t value Pr(>|t|)
#> xmid 1.49945 0.24983 6.002 4.43e-05 ***
#> scal 1.04506 0.09702 10.771 7.55e-08 ***
#> .lin 2.35963 0.23889 9.878 2.08e-07 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> Robust residual standard error: 0.01829
#> Convergence in 10 IRWLS iterations
#>
#> Robustness weights:
#> 14 weights are ~= 1. The remaining 2 ones are
#> 11 13
#> 0.6087 0.7621
## Confidence for linear parameter is quite smaller than "Asym" above
c1 <- coef(summary(RmN1))
c2 <- coef(summary(frm2DNase1))
rownames(c2)[rownames(c2) == ".lin"] <- "Asym"
stopifnot(all.equal(c1[,1:2], c2[rownames(c1), 1:2], tol = 0.09)) # 0.07315
### -- new examples -- "moderate outlier":
DN2 <- DNase1
DN2[10,"density"] <- 2*DN2[10,"density"]
fm3DN2 <- nls(density ~ Asym/(1 + exp(( xmid - log(conc) )/scal ) ),
data = DN2, trace = TRUE,
start = list( Asym = 3, xmid = 0, scal = 1 ))
#> 13.20738 (6.67e+00): par = (3 0 1)
#> 0.4904635 (8.47e-01): par = (1.933442 0.576412 1.054796)
#> 0.2894794 (9.48e-02): par = (2.005496 1.008705 0.9968011)
#> 0.2868991 (2.38e-03): par = (2.043945 1.024726 0.9979448)
#> 0.2868974 (3.46e-04): par = (2.047015 1.028304 0.9997719)
#> 0.2868973 (5.46e-05): par = (2.047365 1.028775 0.9998902)
#> 0.2868973 (8.83e-06): par = (2.047436 1.028867 0.999929)
## robust
Rm3DN2 <- nlrob(density ~ Asym/(1 + exp(( xmid - log(conc) )/scal ) ),
data = DN2, trace = TRUE,
start = list( Asym = 3, xmid = 0, scal = 1 ))
#> robust iteration 1
#> 13.20738 (6.67e+00): par = (3 0 1)
#> 0.4904635 (8.47e-01): par = (1.933442 0.576412 1.054796)
#> 0.2894794 (9.48e-02): par = (2.005496 1.008705 0.9968011)
#> 0.2868991 (2.38e-03): par = (2.043945 1.024726 0.9979448)
#> 0.2868974 (3.46e-04): par = (2.047015 1.028304 0.9997719)
#> 0.2868973 (5.46e-05): par = (2.047365 1.028775 0.9998902)
#> 0.2868973 (8.83e-06): par = (2.047436 1.028867 0.999929)
#> --> irls.delta(previous, resid) = 0.989031 -- *not* converged
#> robust iteration 2
#> 0.1026235 (5.91e-01): par = (2.047436 1.028867 0.999929)
#> 0.07680281 (1.33e-01): par = (2.222549 1.341555 1.042084)
#> 0.07547493 (3.83e-03): par = (2.267845 1.372212 1.042454)
#> 0.07547382 (1.07e-04): par = (2.27053 1.374585 1.043476)
#> 0.07547382 (4.99e-06): par = (2.270591 1.374656 1.043484)
#> --> irls.delta(previous, resid) = 0.335864 -- *not* converged
#> robust iteration 3
#> 0.02400260 (2.23e-01): par = (2.270591 1.374656 1.043484)
#> 0.02286633 (8.28e-03): par = (2.303234 1.423823 1.037888)
#> 0.02286476 (3.87e-05): par = (2.304999 1.424856 1.038261)
#> 0.02286476 (9.14e-07): par = (2.305018 1.424877 1.038266)
#> --> irls.delta(previous, resid) = 0.0669037 -- *not* converged
#> robust iteration 4
#> 0.01583561 (4.08e-02): par = (2.305018 1.424877 1.038266)
#> 0.01580947 (4.45e-04): par = (2.307501 1.428119 1.035495)
#> 0.01580947 (5.55e-06): par = (2.307668 1.42829 1.035585)
#> --> irls.delta(previous, resid) = 0.00966066 -- *not* converged
#> robust iteration 5
#> 0.01595473 (8.06e-03): par = (2.307668 1.42829 1.035585)
#> 0.01595369 (1.15e-04): par = (2.309546 1.430846 1.036013)
#> 0.01595369 (1.99e-06): par = (2.309603 1.430907 1.036034)
#> --> irls.delta(previous, resid) = 0.0020366 -- *not* converged
#> robust iteration 6
#> 0.01574504 (4.05e-03): par = (2.309603 1.430907 1.036034)
#> 0.01574478 (6.15e-05): par = (2.310779 1.432422 1.036364)
#> 0.01574478 (1.05e-06): par = (2.310809 1.432455 1.036375)
#> --> irls.delta(previous, resid) = 0.00101819 -- *not* converged
#> robust iteration 7
#> 0.01561744 (2.08e-03): par = (2.310809 1.432455 1.036375)
#> 0.01561737 (3.13e-05): par = (2.311424 1.43324 1.036545)
#> 0.01561737 (5.46e-07): par = (2.311439 1.433257 1.036551)
#> --> irls.delta(previous, resid) = 0.000522667 -- *not* converged
#> robust iteration 8
#> 0.01555337 (1.06e-03): par = (2.311439 1.433257 1.036551)
#> 0.01555335 (1.57e-05): par = (2.31175 1.433654 1.036636)
#> 0.01555335 (2.56e-07): par = (2.311757 1.433662 1.036639)
#> --> irls.delta(previous, resid) = 0.000264673 -- *not* converged
#> robust iteration 9
#> 0.01552105 (5.32e-04): par = (2.311757 1.433662 1.036639)
#> 0.01552105 (7.89e-06): par = (2.311914 1.433862 1.036682)
#> --> irls.delta(previous, resid) = 0.000132033 -- *not* converged
#> robust iteration 10
#> 0.01550511 (2.70e-04): par = (2.311914 1.433862 1.036682)
#> 0.01550511 (4.04e-06): par = (2.311995 1.433966 1.036705)
#> --> irls.delta(previous, resid) = 6.69939e-05 -- *not* converged
#> robust iteration 11
#> 0.01549687 (1.37e-04): par = (2.311995 1.433966 1.036705)
#> 0.01549687 (2.03e-06): par = (2.312037 1.434019 1.036717)
#> --> irls.delta(previous, resid) = 3.40671e-05 -- *not* converged
#> robust iteration 12
#> 0.01549269 (6.98e-05): par = (2.312037 1.434019 1.036717)
#> 0.01549269 (1.04e-06): par = (2.312058 1.434045 1.036722)
#> --> irls.delta(previous, resid) = 1.72988e-05 -- *not* converged
#> robust iteration 13
#> 0.01549057 (3.55e-05): par = (2.312058 1.434045 1.036722)
#> 0.01549057 (5.21e-07): par = (2.312069 1.434059 1.036725)
#> --> irls.delta(previous, resid) = 8.78386e-06 -- *not* converged
#> robust iteration 14
#> 0.01548949 (1.80e-05): par = (2.312069 1.434059 1.036725)
#> 0.01548949 (3.14e-07): par = (2.312074 1.434066 1.036727)
#> --> irls.delta(previous, resid) = 4.45786e-06 -- *not* converged
#> robust iteration 15
#> 0.01548895 (9.17e-06): par = (2.312074 1.434066 1.036727)
Rm3DN2
#> Robustly fitted nonlinear regression model
#> model: density ~ Asym/(1 + exp((xmid - log(conc))/scal))
#> data: DN2
#> Asym xmid scal
#> 2.312074 1.434066 1.036727
#> status: converged
summary(Rm3DN2) # -> robustness weight of obs. 10 ~= 0.037
#>
#> Call:
#> nlrob(formula = density ~ Asym/(1 + exp((xmid - log(conc))/scal)),
#> data = DN2, start = list(Asym = 3, xmid = 0, scal = 1), trace = TRUE,
#> algorithm = "default")
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.041530 -0.011918 -0.004290 0.008586 0.574492
#>
#> Parameters:
#> Estimate Std. Error t value Pr(>|t|)
#> Asym 2.31207 0.07715 29.97 2.20e-13 ***
#> xmid 1.43407 0.08344 17.19 2.55e-10 ***
#> scal 1.03673 0.03321 31.21 1.31e-13 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> Robust residual standard error: 0.01591
#> Convergence in 15 IRWLS iterations
#>
#> Robustness weights:
#> 12 weights are ~= 1. The remaining 4 ones are
#> 9 10 11 13
#> 0.72536 0.03726 0.81895 0.51538
confint(Rm3DN2, method = "Wald")
#> 0.025 0.975
#> Asym 2.1608716 2.463277
#> xmid 1.2705179 1.597614
#> scal 0.9716313 1.101823
stopifnot(identical(Rm3DN2$dataClasses,
c(density = "numeric", conc = "numeric")))
## utility function sfsmisc::lseq() :
lseq <- function (from, to, length)
2^seq(log2(from), log2(to), length.out = length)
## predict() {and plot}:
h.x <- lseq(min(DN2$conc), max(DN2$conc), length = 100)
nDat <- data.frame(conc = h.x)
h.p <- predict(fm3DN2, newdata = nDat)# classical
h.rp <- predict(Rm3DN2, newdata = nDat)# robust
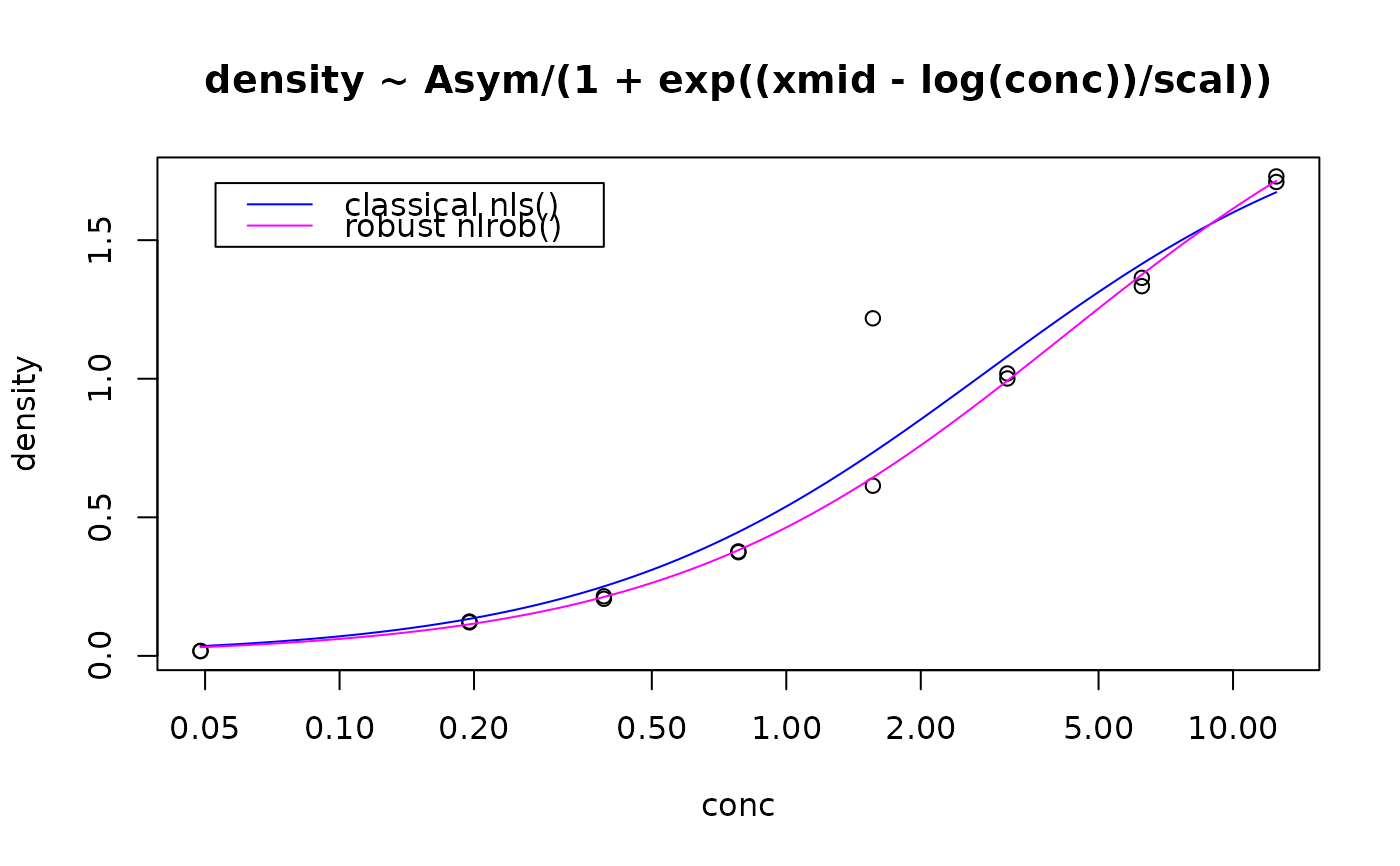
plot(density ~ conc, data=DN2, log="x",
main = format(formula(Rm3DN2)))
lines(h.x, h.p, col="blue")
lines(h.x, h.rp, col="magenta")
legend("topleft", c("classical nls()", "robust nlrob()"),
lwd = 1, col= c("blue", "magenta"), inset = 0.05)
## See ?nlrob.algorithms for examples
# \donttest{
DNase1 <- DNase[DNase$Run == 1,]
form <- density ~ Asym/(1 + exp(( xmid -log(conc) )/scal ))
gMM <- nlrob(form, data = DNase1, method = "MM",
lower = c(Asym = 0, xmid = 0, scal = 0),
upper = 3, trace = TRUE)
#> 1 : < 0.03938195 > ( 0.06412062 ) 1.718003 1.264267 1.218292
#> 2 : < 0.03958695 > ( 0.03402262 ) 2.733063 1.921906 1.119462
#> 3 : < 0.0367546 > ( 0.03402262 ) 2.733063 1.921906 1.119462
#> 4 : < 0.02731668 > ( 0.03402262 ) 2.733063 1.921906 1.119462
#> 5 : < 0.02263389 > ( 0.03402262 ) 2.733063 1.921906 1.119462
#> 6 : < 0.02263389 > ( 0.03402262 ) 2.733063 1.921906 1.119462
#> 7 : < 0.0218549 > ( 0.03402262 ) 2.733063 1.921906 1.119462
#> 8 : < 0.02275302 > ( 0.02916204 ) 2.799944 1.921906 1.119462
#> 9 : < 0.0217358 > ( 0.02916204 ) 2.799944 1.921906 1.119462
#> 10 : < 0.0209807 > ( 0.02916204 ) 2.799944 1.921906 1.119462
#> 11 : < 0.02008903 > ( 0.02916204 ) 2.799944 1.921906 1.119462
#> 12 : < 0.01975389 > ( 0.02486533 ) 2.538736 1.630907 1.081976
#> 13 : < 0.01827828 > ( 0.02486533 ) 2.538736 1.630907 1.081976
#> 14 : < 0.01465184 > ( 0.02486533 ) 2.538736 1.630907 1.081976
#> 15 : < 0.01465184 > ( 0.02486533 ) 2.538736 1.630907 1.081976
#> 16 : < 0.01465184 > ( 0.02486533 ) 2.538736 1.630907 1.081976
#> 17 : < 0.01314939 > ( 0.02486533 ) 2.538736 1.630907 1.081976
#> 18 : < 0.01084913 > ( 0.02486533 ) 2.538736 1.630907 1.081976
#> 19 : < 0.008294563 > ( 0.02486533 ) 2.538736 1.630907 1.081976
#> 20 : < 0.007398615 > ( 0.02059234 ) 2.514683 1.650309 1.106993
#> 21 : < 0.007052105 > ( 0.02059234 ) 2.514683 1.650309 1.106993
#> 22 : < 0.007807116 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 23 : < 0.006530941 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 24 : < 0.005914701 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 25 : < 0.005914701 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 26 : < 0.005186415 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 27 : < 0.005186415 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 28 : < 0.005186415 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 29 : < 0.004746845 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 30 : < 0.004746845 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 31 : < 0.004577892 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 32 : < 0.004577892 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 33 : < 0.004539285 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 34 : < 0.004483952 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 35 : < 0.003637579 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 36 : < 0.003637579 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 37 : < 0.003381681 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 38 : < 0.002646597 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 39 : < 0.002646597 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 40 : < 0.002224195 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 41 : < 0.002224195 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 42 : < 0.002224195 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 43 : < 0.002055919 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 44 : < 0.001657413 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 45 : < 0.001657413 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 46 : < 0.001561297 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 47 : < 0.001561297 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 48 : < 0.001561297 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 49 : < 0.00148575 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 50 : < 0.001454688 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 51 : < 0.001429401 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 52 : < 0.001429401 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 53 : < 0.001231352 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 54 : < 0.001231352 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 55 : < 0.001160419 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 56 : < 0.001036362 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 57 : < 0.001036362 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 58 : < 0.001036362 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 59 : < 0.001036362 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 60 : < 0.001036362 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 61 : < 0.001036362 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 62 : < 0.0009533496 > ( 0.01400308 ) 2.452609 1.630907 1.081976
#> 63 : < 0.000902253 > ( 0.01395297 ) 2.518074 1.679075 1.09572
#> 64 : < 0.000902253 > ( 0.01395297 ) 2.518074 1.679075 1.09572
#> 65 : < 0.001099934 > ( 0.01288313 ) 2.491783 1.668896 1.09214
#> 66 : < 0.001099934 > ( 0.01288313 ) 2.491783 1.668896 1.09214
#> 67 : < 0.001029403 > ( 0.01288313 ) 2.491783 1.668896 1.09214
#> 68 : < 0.001022614 > ( 0.01288313 ) 2.491783 1.668896 1.09214
#> 69 : < 0.0009000824 > ( 0.01288313 ) 2.491783 1.668896 1.09214
#> 70 : < 0.0009000824 > ( 0.01288313 ) 2.491783 1.668896 1.09214
#> 71 : < 0.0008991009 > ( 0.01288313 ) 2.491783 1.668896 1.09214
#> 72 : < 0.0008946788 > ( 0.01288313 ) 2.491783 1.668896 1.09214
#> 73 : < 0.0007602403 > ( 0.01288313 ) 2.491783 1.668896 1.09214
#> 74 : < 0.0007602403 > ( 0.01288313 ) 2.491783 1.668896 1.09214
#> 75 : < 0.0009534746 > ( 0.01162499 ) 2.545471 1.718154 1.108038
#> 76 : < 0.0009534746 > ( 0.01162499 ) 2.545471 1.718154 1.108038
#> 77 : < 0.001084461 > ( 0.0100664 ) 2.535341 1.715352 1.108939
#> 78 : < 0.0009525835 > ( 0.0100664 ) 2.535341 1.715352 1.108939
#> 79 : < 0.0008041755 > ( 0.0100664 ) 2.535341 1.715352 1.108939
#> 80 : < 0.000757977 > ( 0.0100664 ) 2.535341 1.715352 1.108939
#> 81 : < 0.0007280013 > ( 0.0100664 ) 2.535341 1.715352 1.108939
#> 82 : < 0.0006779971 > ( 0.0100664 ) 2.535341 1.715352 1.108939
#> 83 : < 0.0006779971 > ( 0.0100664 ) 2.535341 1.715352 1.108939
#> 84 : < 0.0006779971 > ( 0.0100664 ) 2.535341 1.715352 1.108939
#> 85 : < 0.0006180103 > ( 0.0100664 ) 2.535341 1.715352 1.108939
#> 86 : < 0.0006720913 > ( 0.009773719 ) 2.514275 1.693209 1.106764
#> 87 : < 0.0006720913 > ( 0.009773719 ) 2.514275 1.693209 1.106764
#> 88 : < 0.0006720913 > ( 0.009773719 ) 2.514275 1.693209 1.106764
#> 89 : < 0.0006720913 > ( 0.009773719 ) 2.514275 1.693209 1.106764
#> 90 : < 0.0006720913 > ( 0.009773719 ) 2.514275 1.693209 1.106764
#> 91 : < 0.0005993806 > ( 0.009773719 ) 2.514275 1.693209 1.106764
#> 92 : < 0.0005993806 > ( 0.009773719 ) 2.514275 1.693209 1.106764
#> 93 : < 0.0005400012 > ( 0.009773719 ) 2.514275 1.693209 1.106764
#> 94 : < 0.0005015007 > ( 0.009773719 ) 2.514275 1.693209 1.106764
#> 95 : < 0.0004463291 > ( 0.009412367 ) 2.528438 1.706292 1.110087
#> 96 : < 0.0004463291 > ( 0.009412367 ) 2.528438 1.706292 1.110087
#> 97 : < 0.0003798279 > ( 0.009412367 ) 2.528438 1.706292 1.110087
#> 98 : < 0.0003798279 > ( 0.009412367 ) 2.528438 1.706292 1.110087
#> 99 : < 0.0003798279 > ( 0.009412367 ) 2.528438 1.706292 1.110087
#> 100 : < 0.0003322082 > ( 0.009412367 ) 2.528438 1.706292 1.110087
#> 101 : < 0.0003322082 > ( 0.009412367 ) 2.528438 1.706292 1.110087
#> 102 : < 0.0003077063 > ( 0.009412367 ) 2.528438 1.706292 1.110087
#> 103 : < 0.0003089747 > ( 0.009327055 ) 2.625236 1.789454 1.128951
#> 104 : < 0.000302191 > ( 0.009327055 ) 2.625236 1.789454 1.128951
#> 105 : < 0.0002885228 > ( 0.009298748 ) 2.530553 1.707525 1.112475
#> 106 : < 0.0003472923 > ( 0.00898069 ) 2.535341 1.715352 1.112583
#> 107 : < 0.0003472923 > ( 0.00898069 ) 2.535341 1.715352 1.112583
#> 108 : < 0.0003472923 > ( 0.00898069 ) 2.535341 1.715352 1.112583
#> 109 : < 0.000395383 > ( 0.008720425 ) 2.664996 1.821992 1.138428
#> 110 : < 0.000395383 > ( 0.008720425 ) 2.664996 1.821992 1.138428
#> 111 : < 0.0003101026 > ( 0.008720425 ) 2.664996 1.821992 1.138428
#> 112 : < 0.0002861457 > ( 0.008687433 ) 2.534876 1.715112 1.115454
#> 113 : < 0.0002861457 > ( 0.008687433 ) 2.534876 1.715112 1.115454
#> 114 : < 0.0002861457 > ( 0.008687433 ) 2.534876 1.715112 1.115454
#> 115 : < 0.0002733441 > ( 0.008287295 ) 2.561602 1.74345 1.125946
#> 116 : < 0.0002497225 > ( 0.008161406 ) 2.551418 1.73159 1.120185
#> 117 : < 0.0002391158 > ( 0.008161406 ) 2.551418 1.73159 1.120185
#> 118 : < 0.0002391158 > ( 0.008161406 ) 2.551418 1.73159 1.120185
#> 119 : < 0.0002233379 > ( 0.008161406 ) 2.551418 1.73159 1.120185
#> 120 : < 0.0002159581 > ( 0.008161406 ) 2.551418 1.73159 1.120185
#> 121 : < 0.0002127683 > ( 0.008161406 ) 2.551418 1.73159 1.120185
#> 122 : < 0.0002127683 > ( 0.008161406 ) 2.551418 1.73159 1.120185
#> 123 : < 0.0002127683 > ( 0.008161406 ) 2.551418 1.73159 1.120185
#> 124 : < 0.0001692963 > ( 0.008161406 ) 2.551418 1.73159 1.120185
#> 125 : < 0.0001692963 > ( 0.008161406 ) 2.551418 1.73159 1.120185
#> 126 : < 0.0001487708 > ( 0.008161406 ) 2.551418 1.73159 1.120185
#> 127 : < 0.0001448606 > ( 0.008161406 ) 2.551418 1.73159 1.120185
#> 128 : < 0.0001796217 > ( 0.00797328 ) 2.562922 1.743381 1.125009
#> 129 : < 0.0001783377 > ( 0.00797328 ) 2.562922 1.743381 1.125009
#> 130 : < 0.0001587623 > ( 0.00797328 ) 2.562922 1.743381 1.125009
#> 131 : < 0.0001387313 > ( 0.00797328 ) 2.562922 1.743381 1.125009
#> 132 : < 0.0001387313 > ( 0.00797328 ) 2.562922 1.743381 1.125009
#> 133 : < 0.0001387313 > ( 0.00797328 ) 2.562922 1.743381 1.125009
#> 134 : < 0.0001387313 > ( 0.00797328 ) 2.562922 1.743381 1.125009
#> 135 : < 0.0001263457 > ( 0.00797328 ) 2.562922 1.743381 1.125009
#> 136 : < 0.0001170539 > ( 0.00797328 ) 2.562922 1.743381 1.125009
#> 137 : < 0.0001170539 > ( 0.00797328 ) 2.562922 1.743381 1.125009
#> 138 : < 0.0001130693 > ( 0.00797328 ) 2.562922 1.743381 1.125009
#> 139 : < 9.125206e-05 > ( 0.00797328 ) 2.562922 1.743381 1.125009
#> 140 : < 8.769074e-05 > ( 0.00797328 ) 2.562922 1.743381 1.125009
#> 141 : < 8.769074e-05 > ( 0.00797328 ) 2.562922 1.743381 1.125009
#> 142 : < 8.263095e-05 > ( 0.00797328 ) 2.562922 1.743381 1.125009
#> 143 : < 5.551684e-05 > ( 0.00797328 ) 2.562922 1.743381 1.125009
#> 144 : < 5.611704e-05 > ( 0.007926224 ) 2.564339 1.74422 1.124818
#> 145 : < 3.653528e-05 > ( 0.007926224 ) 2.564339 1.74422 1.124818
#> 146 : < 3.653528e-05 > ( 0.007926224 ) 2.564339 1.74422 1.124818
#> 147 : < 2.582286e-05 > ( 0.007923793 ) 2.564728 1.745004 1.12516
#> 148 : < 2.190055e-05 > ( 0.007923793 ) 2.564728 1.745004 1.12516
#> 149 : < 1.903184e-05 > ( 0.007923793 ) 2.564728 1.745004 1.12516
#> 150 : < 1.885659e-05 > ( 0.007911835 ) 2.565946 1.745953 1.125434
#> 151 : < 1.733574e-05 > ( 0.007911835 ) 2.565946 1.745953 1.125434
#> 152 : < 1.544115e-05 > ( 0.007903055 ) 2.571844 1.75224 1.126482
#> 153 : < 1.149923e-05 > ( 0.007903055 ) 2.571844 1.75224 1.126482
#> 154 : < 1.149923e-05 > ( 0.007903055 ) 2.571844 1.75224 1.126482
#> 155 : < 9.086113e-06 > ( 0.007903055 ) 2.571844 1.75224 1.126482
#> 156 : < 1.106651e-05 > ( 0.007889055 ) 2.569668 1.749645 1.125833
#> 157 : < 9.776442e-06 > ( 0.007889055 ) 2.569668 1.749645 1.125833
#> 158 : < 8.203531e-06 > ( 0.007888029 ) 2.570796 1.750757 1.126876
#> 159 : < 8.203531e-06 > ( 0.007888029 ) 2.570796 1.750757 1.126876
#> 160 : < 9.039615e-06 > ( 0.007883505 ) 2.569799 1.749888 1.126026
#> 161 : < 6.719573e-06 > ( 0.007883505 ) 2.569799 1.749888 1.126026
#> 162 : < 5.215934e-06 > ( 0.007883505 ) 2.569799 1.749888 1.126026
#> 163 : < 4.20277e-06 > ( 0.007883505 ) 2.569799 1.749888 1.126026
#> 164 : < 3.766645e-06 > ( 0.007883505 ) 2.569799 1.749888 1.126026
#> 165 : < 3.602724e-06 > ( 0.007883505 ) 2.569799 1.749888 1.126026
#> 166 : < 3.398271e-06 > ( 0.007883505 ) 2.569799 1.749888 1.126026
#> 167 : < 2.825696e-06 > ( 0.007883505 ) 2.569799 1.749888 1.126026
#> 168 : < 2.825696e-06 > ( 0.007883505 ) 2.569799 1.749888 1.126026
#> 169 : < 2.372335e-06 > ( 0.007883505 ) 2.569799 1.749888 1.126026
#> 170 : < 2.248916e-06 > ( 0.007883505 ) 2.569799 1.749888 1.126026
#> 171 : < 1.961095e-06 > ( 0.007882063 ) 2.571564 1.7516 1.126749
#> 172 : < 1.581348e-06 > ( 0.007882063 ) 2.571564 1.7516 1.126749
#> 173 : < 1.351087e-06 > ( 0.007880429 ) 2.569868 1.749998 1.126216
#> 174 : < 1.242324e-06 > ( 0.007880429 ) 2.569868 1.749998 1.126216
#> 175 : < 1.242324e-06 > ( 0.007880429 ) 2.569868 1.749998 1.126216
#> 176 : < 1.144362e-06 > ( 0.007880429 ) 2.569868 1.749998 1.126216
#> 177 : < 1.144362e-06 > ( 0.007880429 ) 2.569868 1.749998 1.126216
#> 178 : < 1.144362e-06 > ( 0.007880429 ) 2.569868 1.749998 1.126216
#> 179 : < 1.144362e-06 > ( 0.007880429 ) 2.569868 1.749998 1.126216
#> 180 : < 1.144362e-06 > ( 0.007880429 ) 2.569868 1.749998 1.126216
#> 181 : < 9.158362e-07 > ( 0.007880429 ) 2.569868 1.749998 1.126216
## "CM" (and "mtl") additionally need bounds for "sigma" :
gCM <- nlrob(form, data = DNase1, method = "CM",
lower = c(Asym = 0, xmid = 0, scal = 0, sigma = 0),
upper = c(3,3,3, sigma = 0.8))
summary(gCM)# did fail; note it has NA NA NA (std.err, t val, P val)
#>
#> Call:
#> nlrob(formula = form, data = DNase1, lower = c(Asym = 0, xmid = 0,
#> scal = 0, sigma = 0), upper = c(3, 3, 3, sigma = 0.8), method = "CM")
#>
#> Method "CM", psi = "bisquare"
#> Residuals:
#> 1 2 3 4 5 6 7
#> -0.0140292 -0.0130292 0.0084722 0.0114722 -0.0028066 0.0061934 0.0032156
#> 8 9 10 11 12 13 14
#> 0.0002156 -0.0169468 -0.0219468 0.0409223 0.0229223 -0.0316757 -0.0016757
#> 15 16
#> 0.0134027 -0.0065973
#>
#> Parameters:
#> Estimate Std. Error t value Pr(>|t|)
#> Asym 2.36379 NA NA NA
#> xmid 1.50426 NA NA NA
#> scal 1.04718 NA NA NA
#> sigma 0.08045 NA NA NA
#>
#> Robust residual standard error: 0.08045
#> Convergence
#>
stopifnot(identical(Rm3DN2$dataClasses, gMM$dataClasses),
identical( gCM$dataClasses, gMM$dataClasses))
# }