Smooth Weighting Function - Generalized Biweight

“The Biweight on a Stick” — Compute a smooth (when \(h > 0\)) weight function typically for computing weights from large (robust) “distances” using a piecewise polynomial function which in fact is a 2-parameter generalization of Tukey's 1-parameter “biweight”.

smoothWgt(x, c, h)

Arguments

x

numeric vector of abscissa values

c

“cutoff”, a typically positive number.

h

“bandwidth”, a positive number.

Details

Let \(w(x;c,h) := \)smoothWgt(x, c, h). Then, $$% "FIXME": rather use amsmath package \cases{.} w(x; c,h) := 0 \ \ \ \ \ \mathrm{if}\ |x| \ge c + h/2,$$ $$ w(x; c,h) := 1 \ \ \ \ \ \mathrm{if}\ |x| \le c - h/2,$$ $$ w(x; c,h) := \bigl((1 - |x| - (c-h/2))^2\bigr)^2 \ \mathrm{if}\ c-h/2 < |x| < c+h/2,$$

smoothWgt() is scale invariant in the sense that $$w(\sigma x; \sigma c, \sigma h) = w(x; c, h),$$ when \(\sigma > 0\).

Value

a numeric vector of the same length as x with weights between zero and one. Currently all attributes including dim and names are dropped.

Author

Martin Maechler

See also

Mwgt(.., psi = "bisquare") of which smoothWgt() is a generalization, and Mwgt(.., psi = "optimal") which looks similar for larger c with its constant one part around zero, but also has only one parameter.

Examples

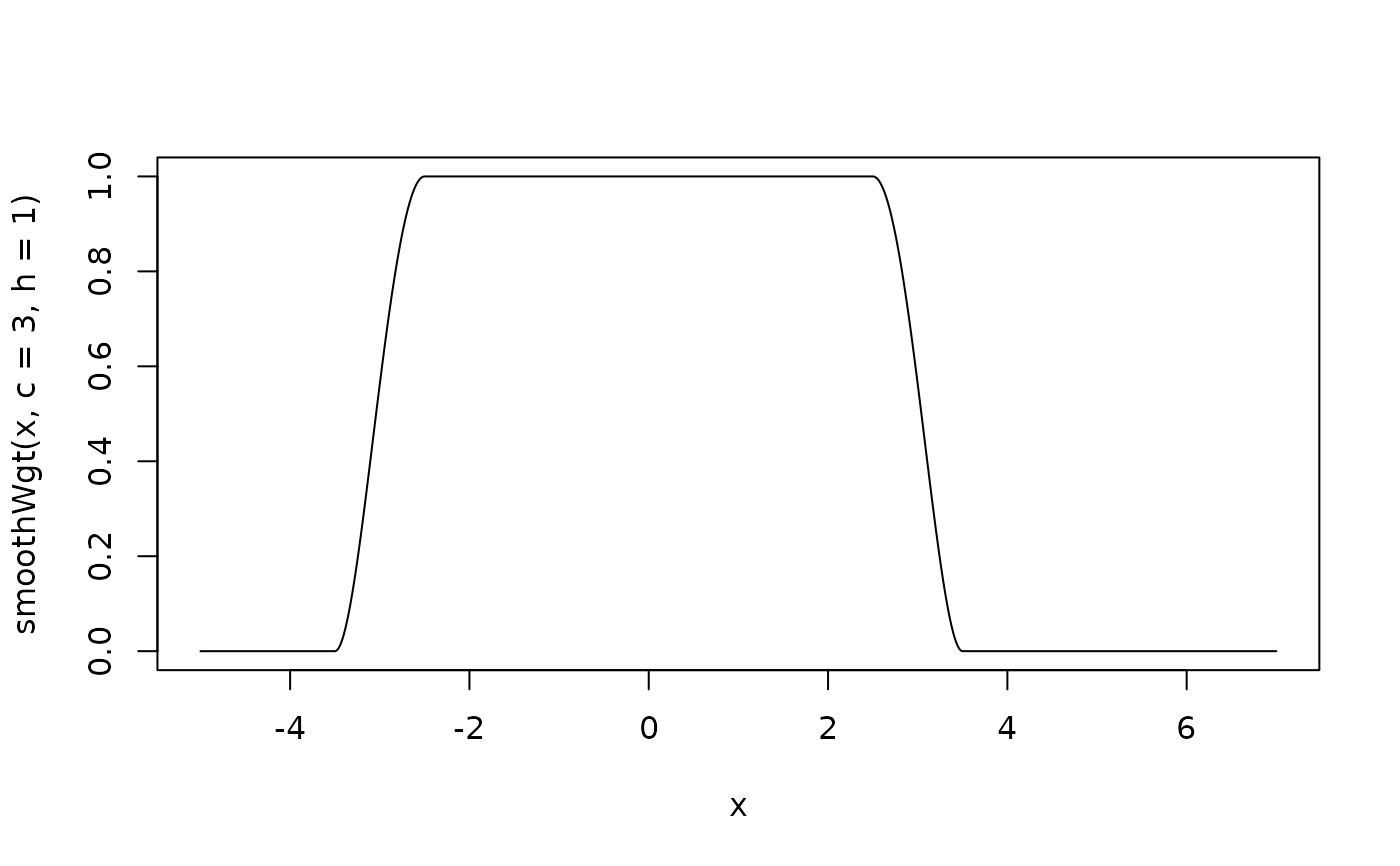
## a somewhat typical picture:
curve(smoothWgt(x, c=3, h=1), -5,7, n = 1000)


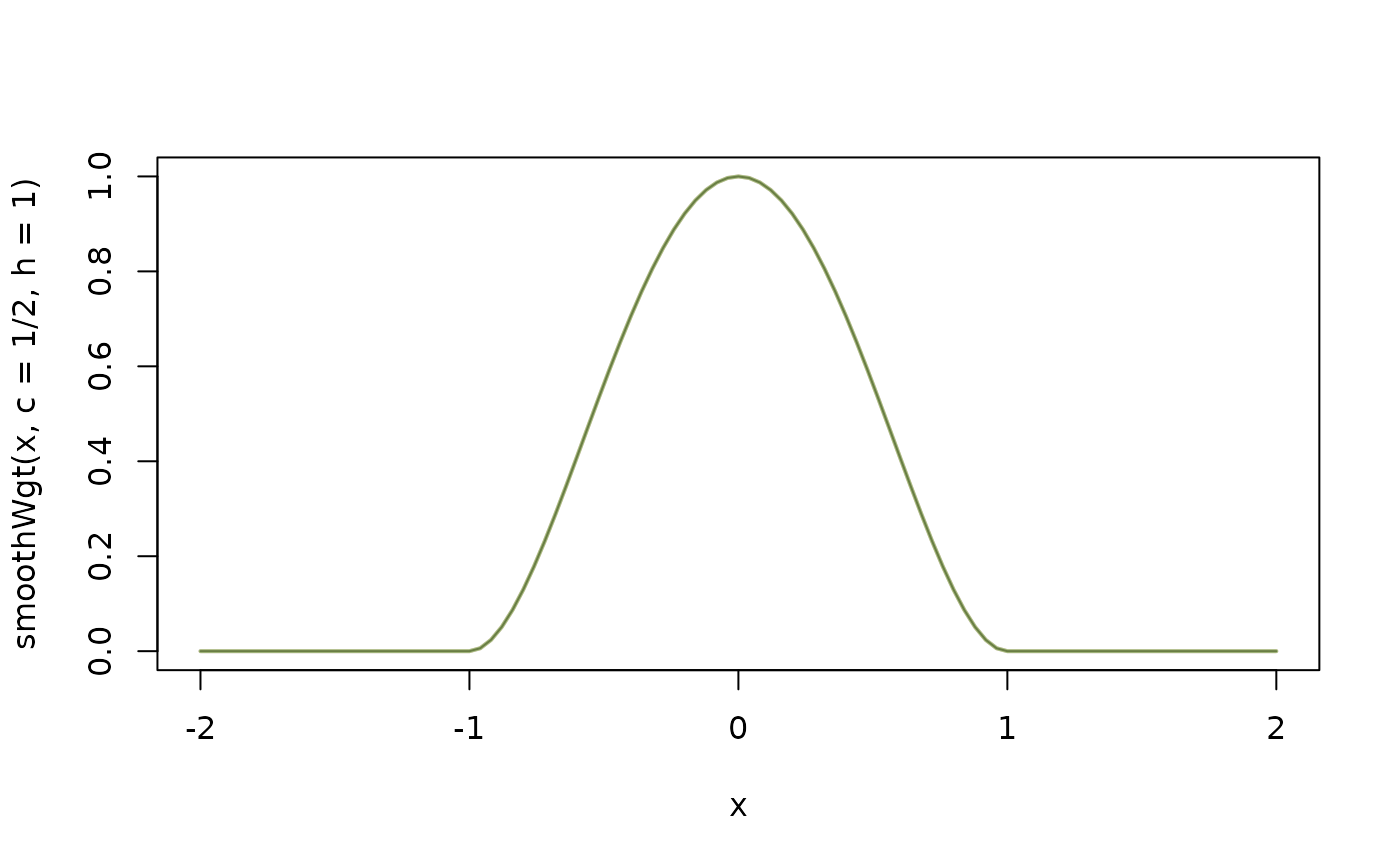
csW <- curve(smoothWgt(x, c=1/2, h=1), -2,2) # cutoff 1/2, bandwidth 1
## Show that the above is the same as
## Tukey's "biweight" or "bi-square" weight function:
bw <- function(x) pmax(0, (1 - x^2))^2
cbw <- curve(bw,                     col=adjustcolor(2, 1/2), lwd=2, add=TRUE)
cMw <- curve(Mwgt(x,c=1,"biweight"), col=adjustcolor(3, 1/2), lwd=2, add=TRUE)

stopifnot(## proving they are all the same:
   all.equal(csW, cbw, tol=1e-15),
   all.equal(csW, cMw, tol=1e-15))