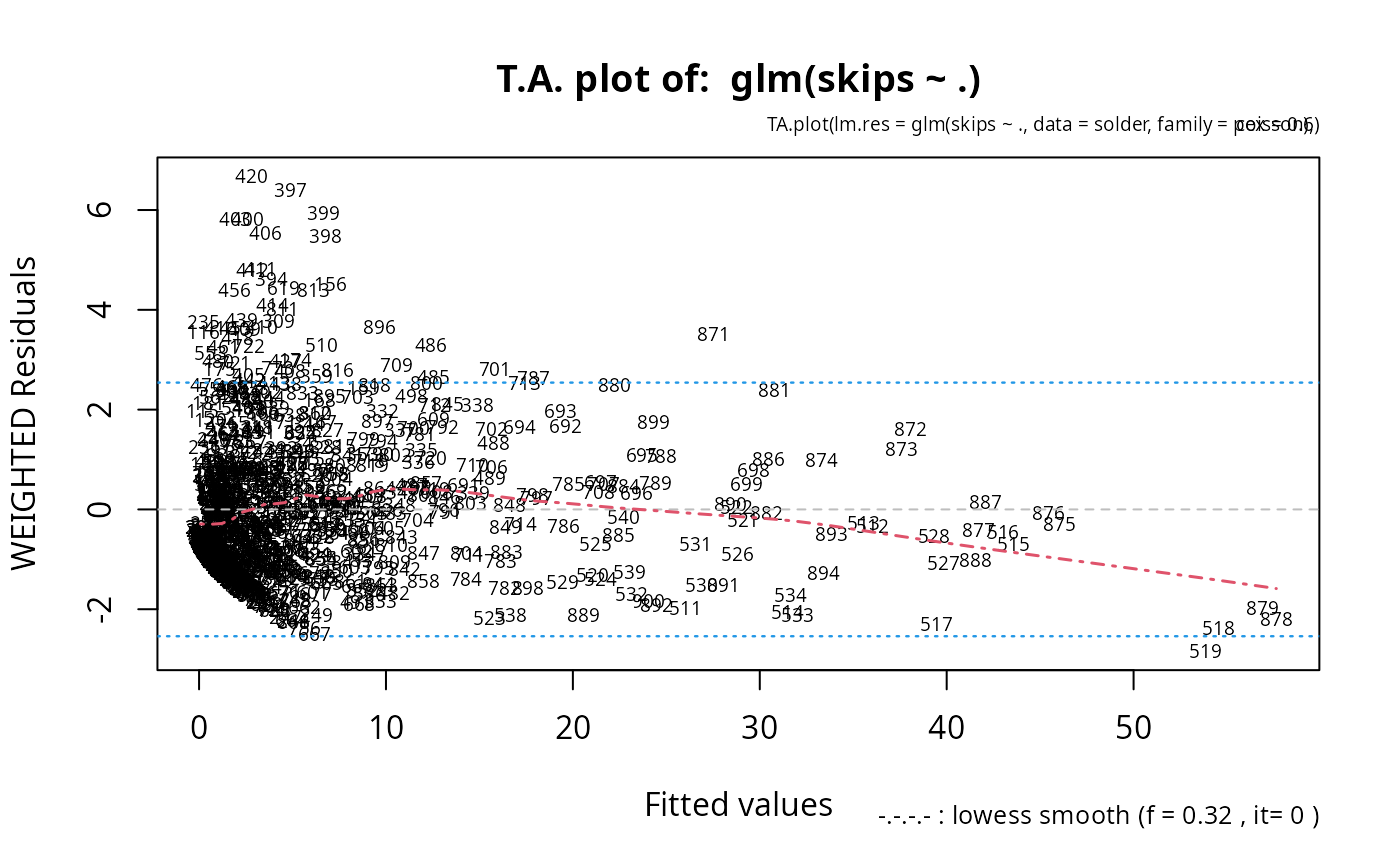
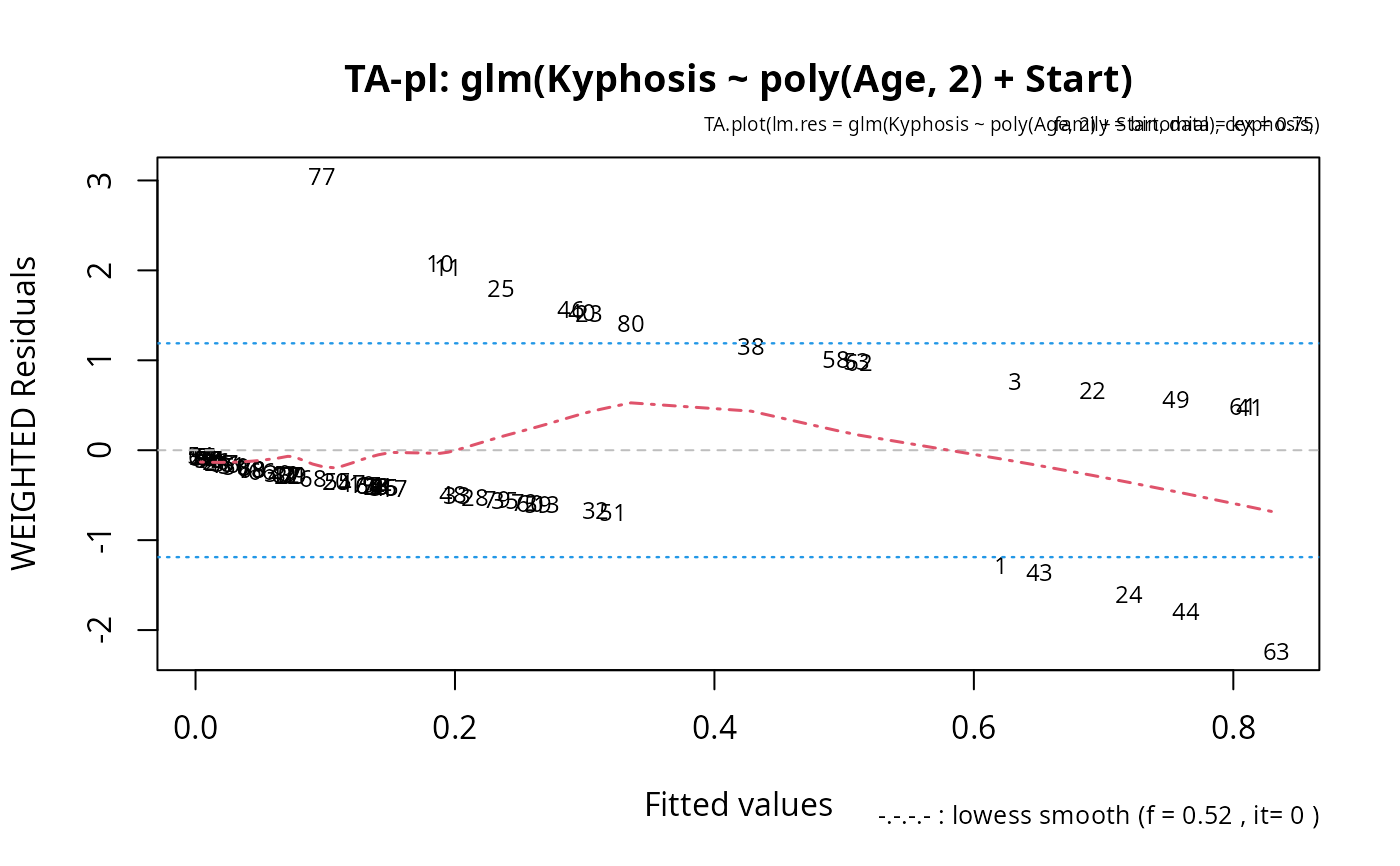
Tukey-Anscombe Plot (Residual vs. Fitted) of a Linear Model

From a linear (or glm) model fitted, produce the so-called Tukey-Anscombe plot. Useful (optional) additions include: 0-line, lowess smooth, 2sigma lines, and automatic labeling of observations.

Usage

TA.plot(lm.res,
        fit= fitted(lm.res), res= residuals(lm.res, type="pearson"),
        labels= NULL, main= mk.main(), xlab = "Fitted values",
        draw.smooth= n >= 10, show.call = TRUE, show.2sigma= TRUE,
        lo.iter = NULL, lo.cex= NULL,
        par0line  = list(lty = 2, col = "gray"),
        parSmooth = list(lwd = 1.5, lty = 4, col = 2),
        parSigma  = list(lwd = 1.2, lty = 3, col = 4),
        verbose = FALSE,
        ...)

Arguments

lm.res: Result of lm(..), aov(..), glm(..) or a similar object.
fit: fitted values; you probably want the default here.
res: residuals to use. Default: Weighted ("Pearson") residuals if weights have been used for the model fit.
labels: strings to use as plotting symbols for each point. Default(NULL): extract observations' names or use its sequence number. Use, e.g., "*" to get simple * symbols.
main: main title to plot. Default: sophisticated, resulting in something like "Tukey-Anscombe Plot of : y ~ x" constructed from lm.res $ call.
xlab: x-axis label for plot.
draw.smooth: logical; if TRUE, draw a lowess smoother (with automatic smoothing fraction).
show.call: logical; if TRUE, write the "call"ing syntax with which the fit was done.
show.2sigma: logical; if TRUE, draw horizontal lines at $\pm 2\sigma$ where $\sigma$ is mad(resid).
lo.iter: positive integer, giving the number of lowess robustness iterations. The default depends on the model and is 0 for non Gaussian glm's.
lo.cex: character expansion ("cex") for lowess and other marginal texts.
par0line: a list of arguments (with reasonable defaults) to be passed to abline(.) when drawing the x-axis, i.e., the $y = 0$ line.
parSmooth, parSigma: each a list of arguments (with reasonable default) for drawing the smooth curve (if draw.smooth is true), or the horizontal sigma boundaries (if show.2sigma is true) respectively.
verbose: logical indicating if some construction details should be reported (print()ed).
...: further graphical parameters are passed to n.plot(.).

Side Effects

The above mentioned plot is produced on the current graphic device.

Author

Martin Maechler, Seminar fuer Statistik, ETH Zurich, Switzerland; maechler@stat.math.ethz.ch

Examples

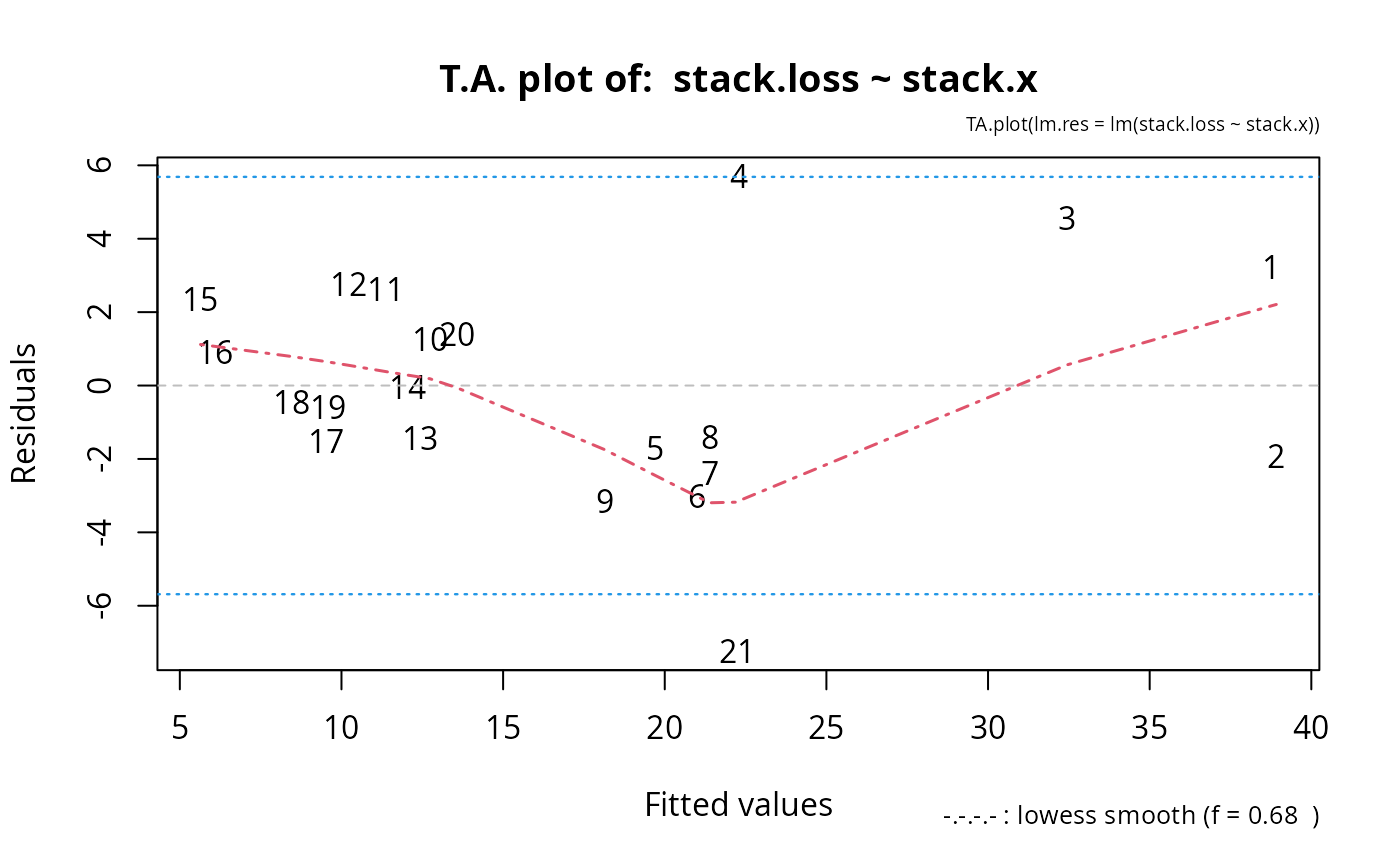
data(stackloss)
TA.plot(lm(stack.loss ~ stack.x))


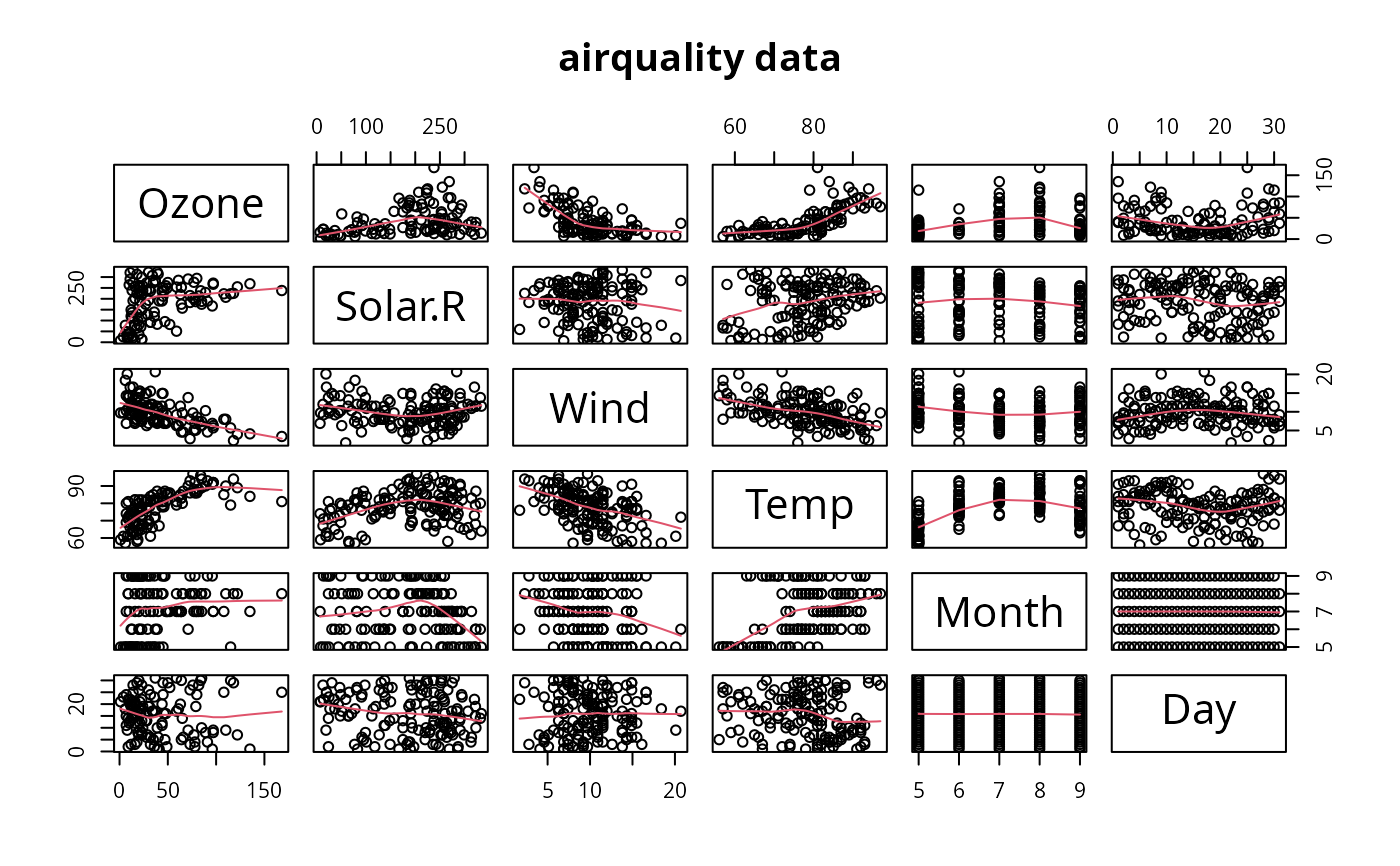
example(airquality)
#> 
#> arqlty> require(graphics)
#> 
#> arqlty> pairs(airquality, panel = panel.smooth, main = "airquality data")

summary(lmO <- lm(Ozone ~ ., data= airquality))
#> 
#> Call:
#> lm(formula = Ozone ~ ., data = airquality)
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -37.014 -12.284  -3.302   8.454  95.348 
#> 
#> Coefficients:
#>              Estimate Std. Error t value Pr(>|t|)    
#> (Intercept) -64.11632   23.48249  -2.730  0.00742 ** 
#> Solar.R       0.05027    0.02342   2.147  0.03411 *  
#> Wind         -3.31844    0.64451  -5.149 1.23e-06 ***
#> Temp          1.89579    0.27389   6.922 3.66e-10 ***
#> Month        -3.03996    1.51346  -2.009  0.04714 *  
#> Day           0.27388    0.22967   1.192  0.23576    
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> Residual standard error: 20.86 on 105 degrees of freedom
#>   (42 observations deleted due to missingness)
#> Multiple R-squared:  0.6249,	Adjusted R-squared:  0.6071 
#> F-statistic: 34.99 on 5 and 105 DF,  p-value: < 2.2e-16
#> 
TA.plot(lmO)

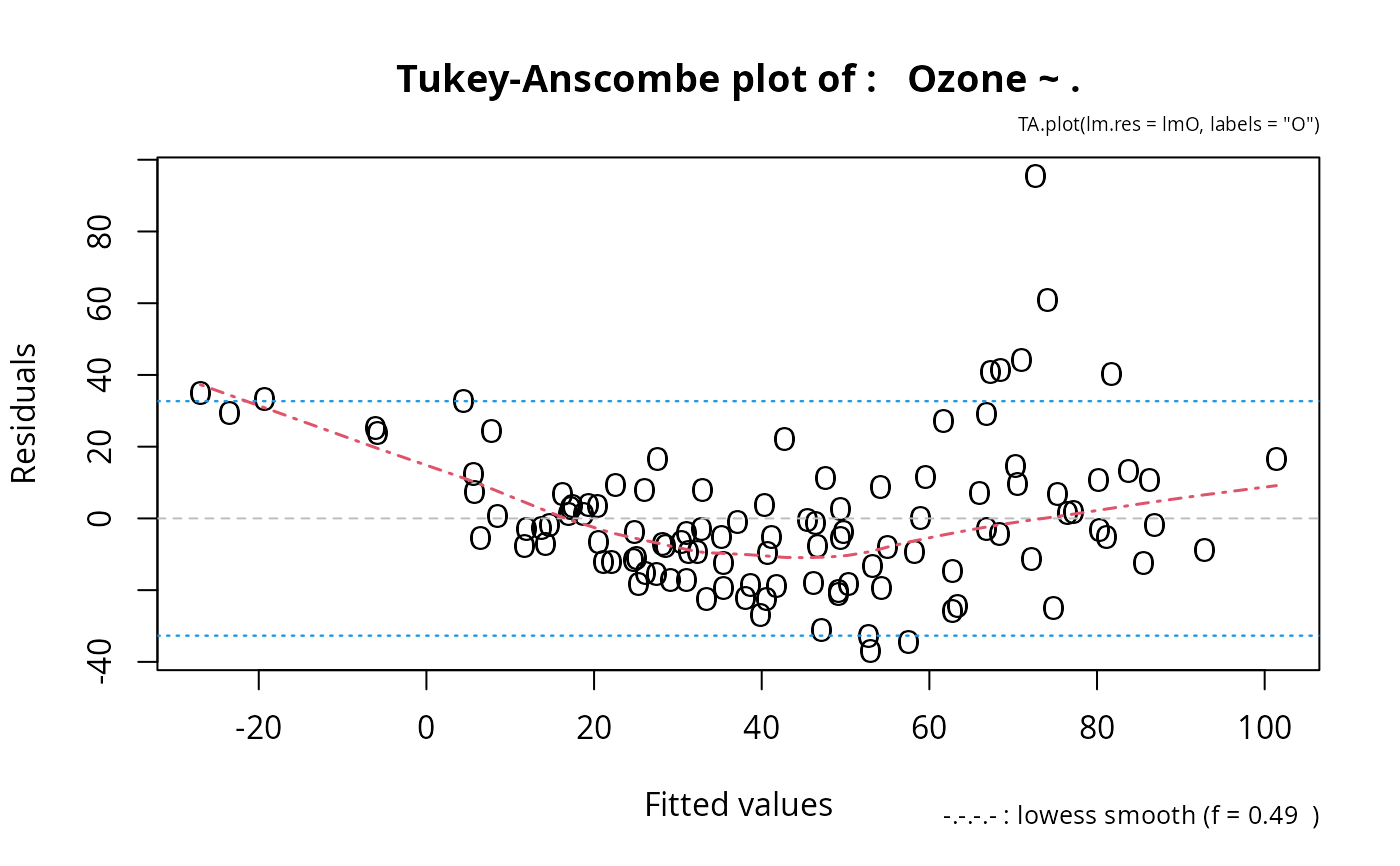
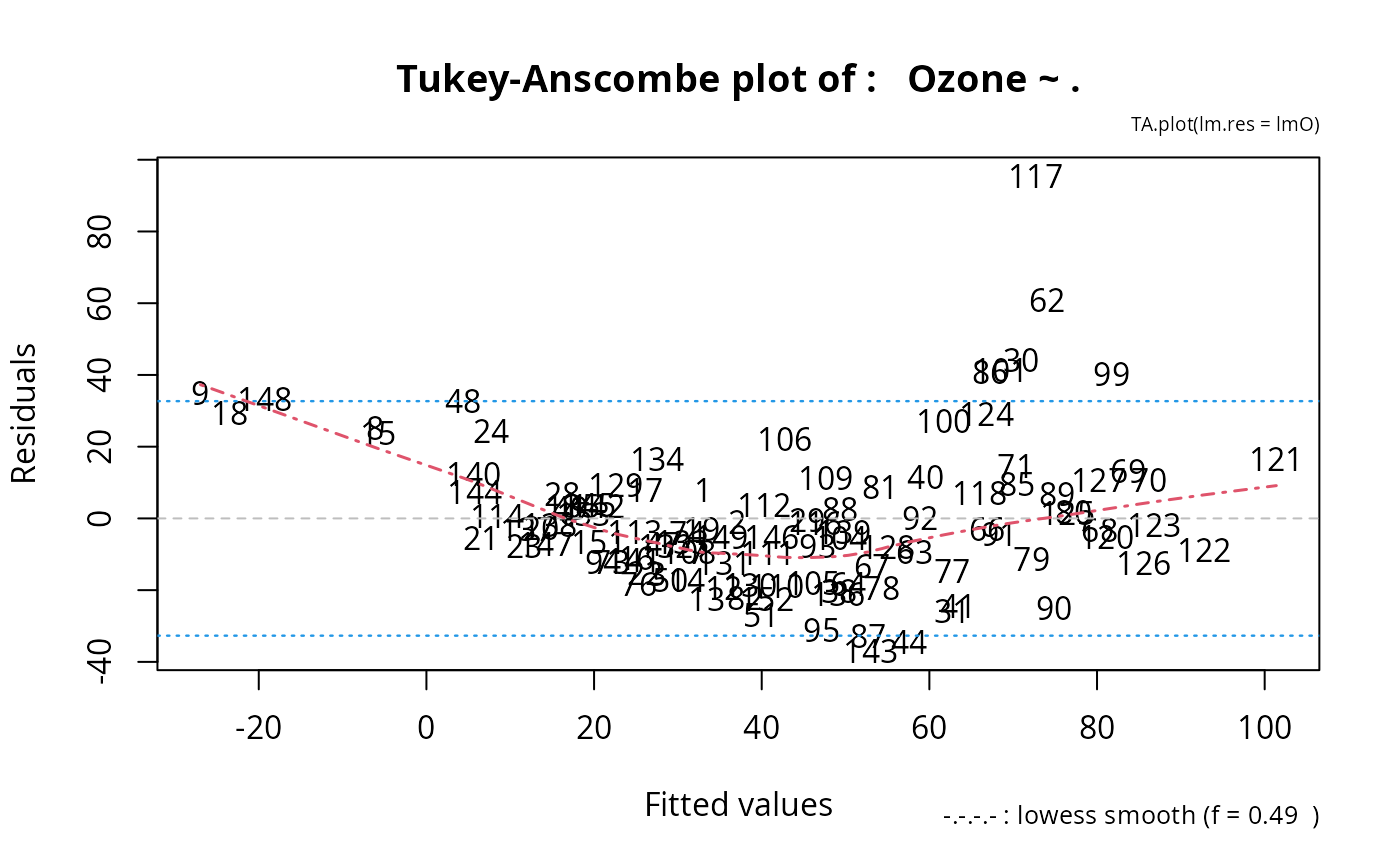TA.plot(lmO, label = "O") # instead of case numbers


if(FALSE) { 
 TA.plot(lm(cost ~ age+type+car.age, claims, weights=number, na.action=na.omit))
}

##--- for  aov(.) : -------------
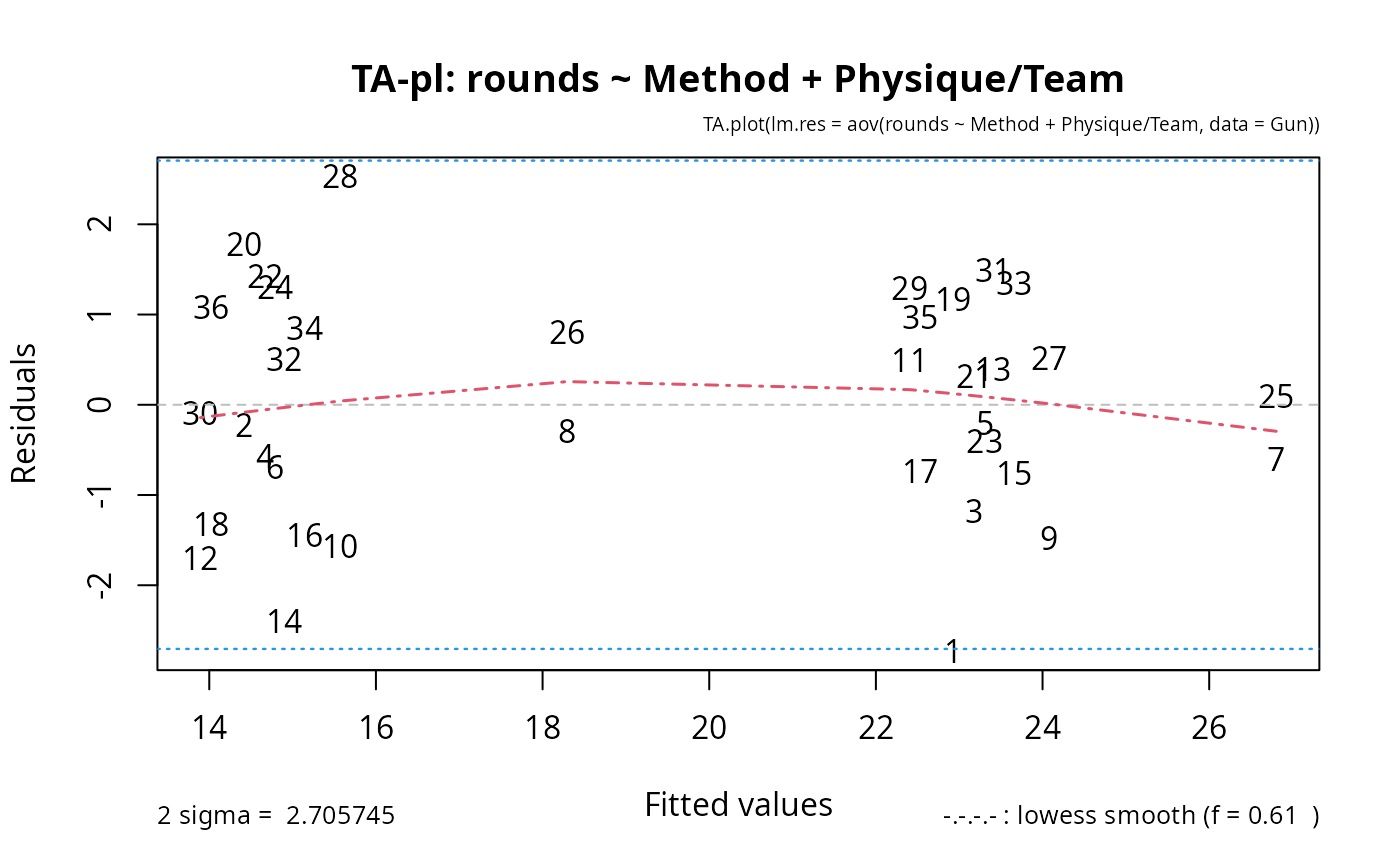
data(Gun, package = "nlme")
TA.plot( aov(rounds ~ Method + Physique/Team, data = Gun))


##--- Not so clear what it means for GLM, but: ------
if(require(rpart)) { # for the two datasets only
 data(solder, package = "rpart")
 TA.plot(glm(skips ~ ., data = solder, family = poisson), cex= .6)

 data(kyphosis, package = "rpart")
 TA.plot(glm(Kyphosis ~ poly(Age,2) + Start, data=kyphosis, family = binomial),
   cex=.75) # smaller title and plotting characters
}
#> Loading required package: rpart