Find all Primes Less Than n

Find all prime numbers aka ‘primes’ less than $n$.

Uses an obvious sieve method (and some care), working with logical and and integers to be quite fast.

Usage

primes(n, pSeq = NULL)

Arguments

n: a (typically positive integer) number.
pSeq: optionally a vector of primes (2,3,5,...) as if from a primes() call; must be correct. The goal is a speedup, but currently we have not found one single case, where using a non-NULL pSeq is faster.

Details

As the function only uses max(n), n can also be a vector of numbers.

The famous prime number theorem states that $\pi(n)$, the number of primes below $n$ is asymptotically $n / \log(n)$ in the sense that $\lim_{n \to \infty}{\pi(n) \cdot \log(n) / n \sim 1}$.

Equivalently, the inverse of $pi()$, the $n$-th prime number $p_n$ is around $n \log n$; recent results (Pierre Dusart, 1999), prove that $$\log n + \log\log n - 1 < \frac{p_n}{n} < \log n + \log \log n \quad\mathrm{for } n \ge 6.$$

Value

numeric vector of all prime numbers $\le n$.

Author

Bill Venables (<= 2001); Martin Maechler gained another 40% speed, carefully working with logicals and integers.

Examples

 (p1 <- primes(100))
#>  [1]  2  3  5  7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97
 system.time(p1k <- primes(1000)) # still lightning fast
#>    user  system elapsed 
#>   0.003   0.000   0.003 
 stopifnot(length(p1k) == 168)
# \donttest{
 system.time(p.e7 <- primes(1e7)) # still only 0.3 sec (2015 (i7))
#>    user  system elapsed 
#>   0.412   0.031   0.443 
 stopifnot(length(p.e7) == 664579)
 ## The famous  pi(n) :=  number of primes <= n:
 pi.n <- approxfun(p.e7, seq_along(p.e7), method = "constant")
 pi.n(c(10, 100, 1000)) # 4 25 168
#> [1]   4  25 168
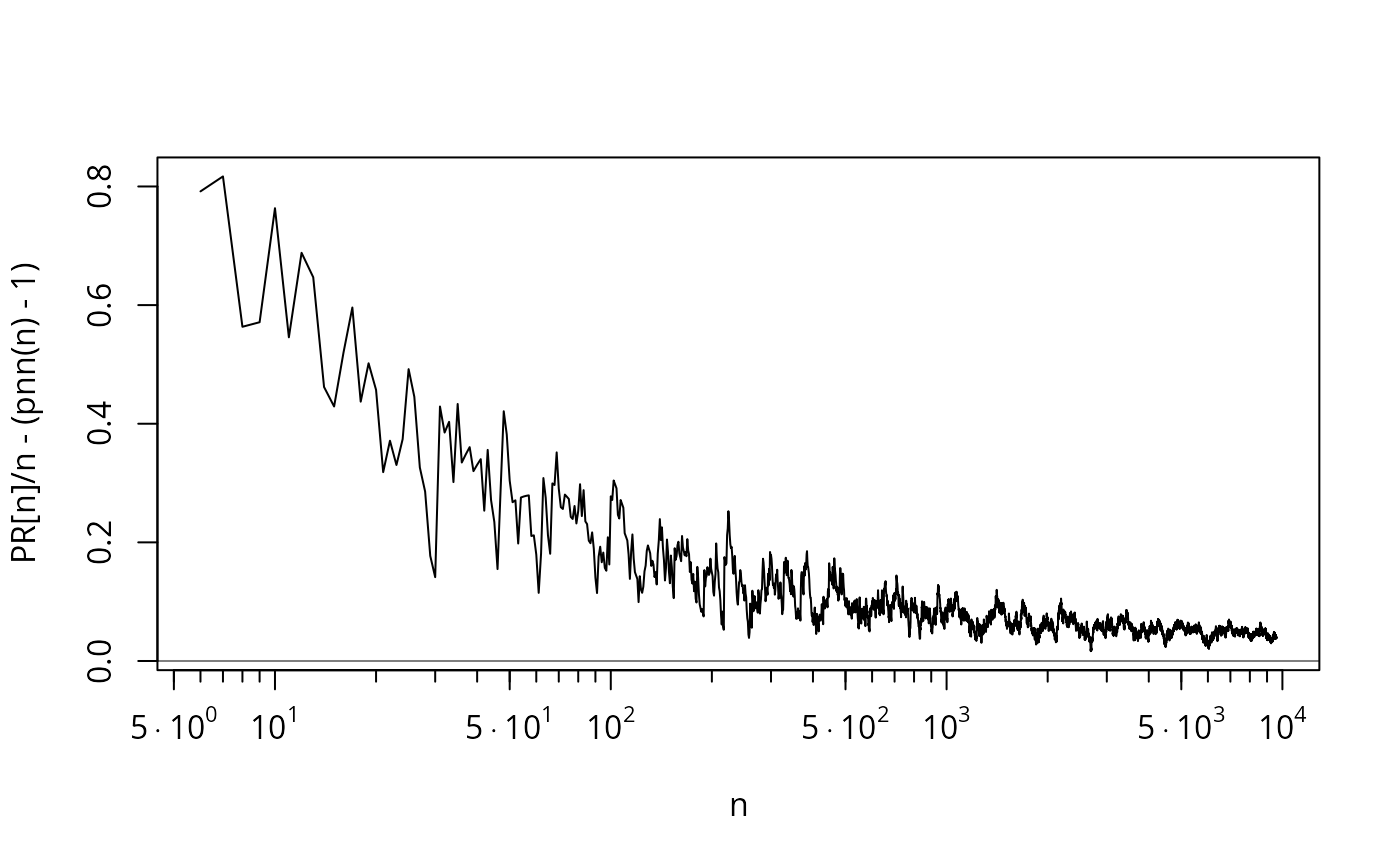
 plot(pi.n, 2, 1e7, n = 1024, log="xy", axes = FALSE,
      xlab = "n", ylab = quote(pi(n)),
      main = quote("The prime number function " ~ pi(n)))
 eaxis(1); eaxis(2)

# }

## Exploring  p(n) := the n-th prime number  ~=~ n * pnn(n), where
## pnn(n) := log n + log log n
pnn <- function(n) { L <- log(n); L + log(L) }
n <- 6:(N <- length(PR <- primes(1e5)))
m.pn <- cbind(l.pn = ceiling(n*(pnn(n)-1)), pn = PR[n], u.pn = floor(n*pnn(n)))
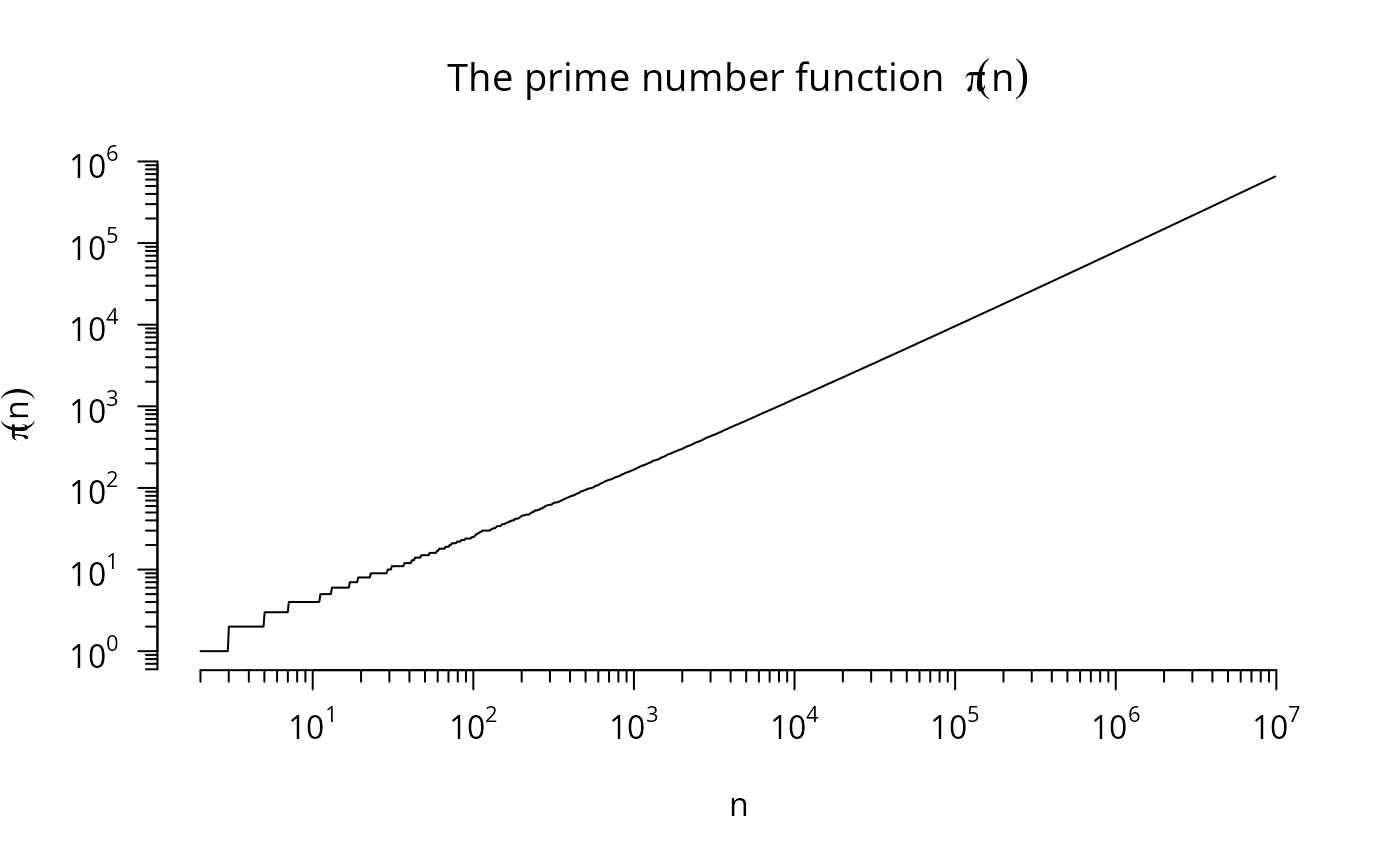
matplot(n, m.pn, type="l", ylab = quote(p[n]), main = quote(p[n] ~~
        "with lower/upper bounds" ~ n*(log(n) + log(log(n)) -(1~"or"~0))))

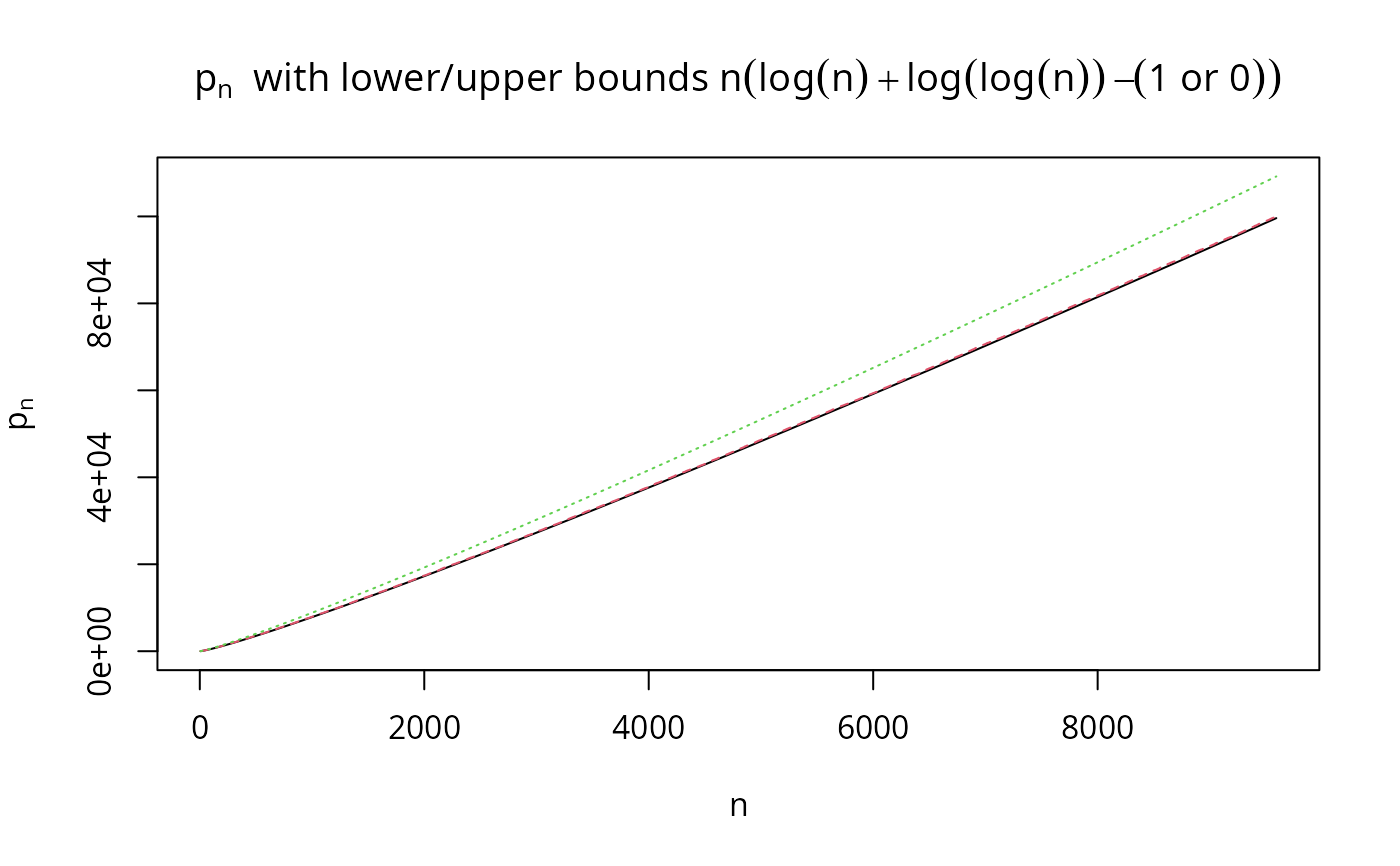## (difference to the lower approximation) / n   --> ~ 0.0426  (?) :
plot(n, PR[n]/n - (pnn(n)-1), type = 'l', cex = 1/8, log="x", xaxt="n")
eaxis(1); abline(h=0, col=adjustcolor(1, 0.5))