Methods in Package Matrix for Function solve
solve-methods.RdMethods for generic function solve for solving
linear systems of equations,
i.e., for \(X\) in \(A X = B\),
where \(A\) is a square matrix and \(X\) and \(B\) are matrices
with dimensions consistent with \(A\).
solve(a, b, ...)
# S4 method for class 'dgeMatrix,ANY'
solve(a, b, tol = .Machine$double.eps, ...)
# S4 method for class 'dgCMatrix,missing'
solve(a, b, sparse = TRUE, ...)
# S4 method for class 'dgCMatrix,matrix'
solve(a, b, sparse = FALSE, ...)
# S4 method for class 'dgCMatrix,denseMatrix'
solve(a, b, sparse = FALSE, ...)
# S4 method for class 'dgCMatrix,sparseMatrix'
solve(a, b, sparse = TRUE, ...)
# S4 method for class 'denseLU,dgeMatrix'
solve(a, b, ...)
# S4 method for class 'BunchKaufman,dgeMatrix'
solve(a, b, ...)
# S4 method for class 'Cholesky,dgeMatrix'
solve(a, b, ...)
# S4 method for class 'sparseLU,dgCMatrix'
solve(a, b, tol = .Machine$double.eps, ...)
# S4 method for class 'sparseQR,dgCMatrix'
solve(a, b, ...)
# S4 method for class 'CHMfactor,dgCMatrix'
solve(a, b, system = c("A", "LDLt", "LD", "DLt", "L", "Lt", "D", "P", "Pt"), ...)Arguments
- a
a finite square matrix or
Matrixcontaining the coefficients of the linear system, or otherwise aMatrixFactorization, in which case methods behave (by default) as if the factorized matrix were specified.- b
a vector,
sparseVector, matrix, orMatrixsatisfyingNROW(b) == nrow(a), giving the right-hand side(s) of the linear system. Vectorsbare treated aslength(b)-by-1 matrices. Ifbis missing, then methods takebto be an identity matrix.- tol
a non-negative number. For
ainheriting fromdenseMatrix, an error is signaled if the reciprocal one-norm condition number (seercond) ofais less thantol, indicating thatais near-singular. Foraof classsparseLU, an error is signaled if the ratiomin(d)/max(d)is less thantol, whered = abs(diag(a@U)). (Interpret with care, as this ratio is a cheap heuristic and not in general equal to or even proportional to the reciprocal one-norm condition number.) Settingtol = 0disables the test.- sparse
a logical indicating if the result should be formally sparse, i.e., if the result should inherit from virtual class
sparseMatrix. Only methods for sparseaand missing or matrixbhave this argument. Methods for missing or sparsebusesparse = TRUEby default. Methods for densebusesparse = FALSEby default.- system
a string specifying a linear system to be solved. Only methods for
ainheriting fromCHMfactorhave this argument. See ‘Details’.- ...
further arguments passed to or from methods.
Details
Methods for general and symmetric matrices a compute a
triangular factorization (LU, Bunch-Kaufman, or Cholesky)
and call the method for the corresponding factorization class.
The factorization is sparse if a is. Methods for sparse,
symmetric matrices a attempt a Cholesky factorization
and perform an LU factorization only if that fails (typically
because a is not positive definite).
Triangular, diagonal, and permutation matrices do not require
factorization (they are already “factors”), hence methods
for those are implemented directly. For triangular a,
solutions are obtained by forward or backward substitution;
for diagonal a, they are obtained by scaling the rows
of b; and for permutations a, they are obtained
by permuting the rows of b.
Methods for dense a are built on 14 LAPACK routines:
class d..Matrix, where ..=(ge|tr|tp|sy|sp|po|pp),
uses routines d..tri and d..trs for missing
and non-missing b, respectively. A corollary is that
these methods always give a dense result.
Methods for sparse a are built on CXSparse routines
cs_lsolve, cs_usolve, and cs_spsolve and
CHOLMOD routines cholmod_solve and cholmod_spsolve.
By default, these methods give a vector result if b
is a vector, a sparse matrix result if b is missing
or a sparse matrix, and a dense matrix result if b
is a dense matrix. One can override this behaviour by setting
the sparse argument, where available, but that should
be done with care. Note that a sparse result may be sparse only
in the formal sense and not at all in the mathematical sense,
depending on the nonzero patterns of a and b.
Furthermore, whereas dense results are fully preallocated,
sparse results must be “grown” in a loop over the columns
of b.
Methods for a of class sparseQR
are simple wrappers around qr.coef, giving the
least squares solution in overdetermined cases.
Methods for a inheriting from CHMfactor
can solve systems other than the default one \(A X = B\).
The correspondence between its system argument the system
actually solved is outlined in the table below.
See CHMfactor-class for a definition of notation.
system | isLDL(a)=TRUE | isLDL(a)=FALSE |
"A" | \(A X = B\) | \(A X = B\) |
"LDLt" | \(L_{1} D L_{1}' X = B\) | \(L L' X = B\) |
"LD" | \(L_{1} D X = B\) | \(L X = B\) |
"DLt" | \(D L_{1}' X = B\) | \(L' X = B\) |
"L" | \(L_{1} X = B\) | \(L X = B\) |
"Lt" | \(L_{1}' X = B\) | \(L' X = B\) |
"D" | \(D X = B\) | \(X = B\) |
"P" | \(X = P_{1} B\) | \(X = P_{1} B\) |
"Pt" | \(X = P_{1}' B\) | \(X = P_{1}' B\) |
See also
Virtual class MatrixFactorization and its
subclasses.
Generic functions Cholesky, BunchKaufman,
Schur, lu, and qr for
computing factorizations.
Generic function solve from base.
Function qr.coef from base for computing
least squares solutions of overdetermined linear systems.
Examples
## A close to symmetric example with "quite sparse" inverse:
n1 <- 7; n2 <- 3
dd <- data.frame(a = gl(n1,n2), b = gl(n2,1,n1*n2))# balanced 2-way
X <- sparse.model.matrix(~ -1+ a + b, dd)# no intercept --> even sparser
XXt <- tcrossprod(X)
diag(XXt) <- rep(c(0,0,1,0), length.out = nrow(XXt))
n <- nrow(ZZ <- kronecker(XXt, Diagonal(x=c(4,1))))
image(a <- 2*Diagonal(n) + ZZ %*% Diagonal(x=c(10, rep(1, n-1))))
 isSymmetric(a) # FALSE
#> [1] FALSE
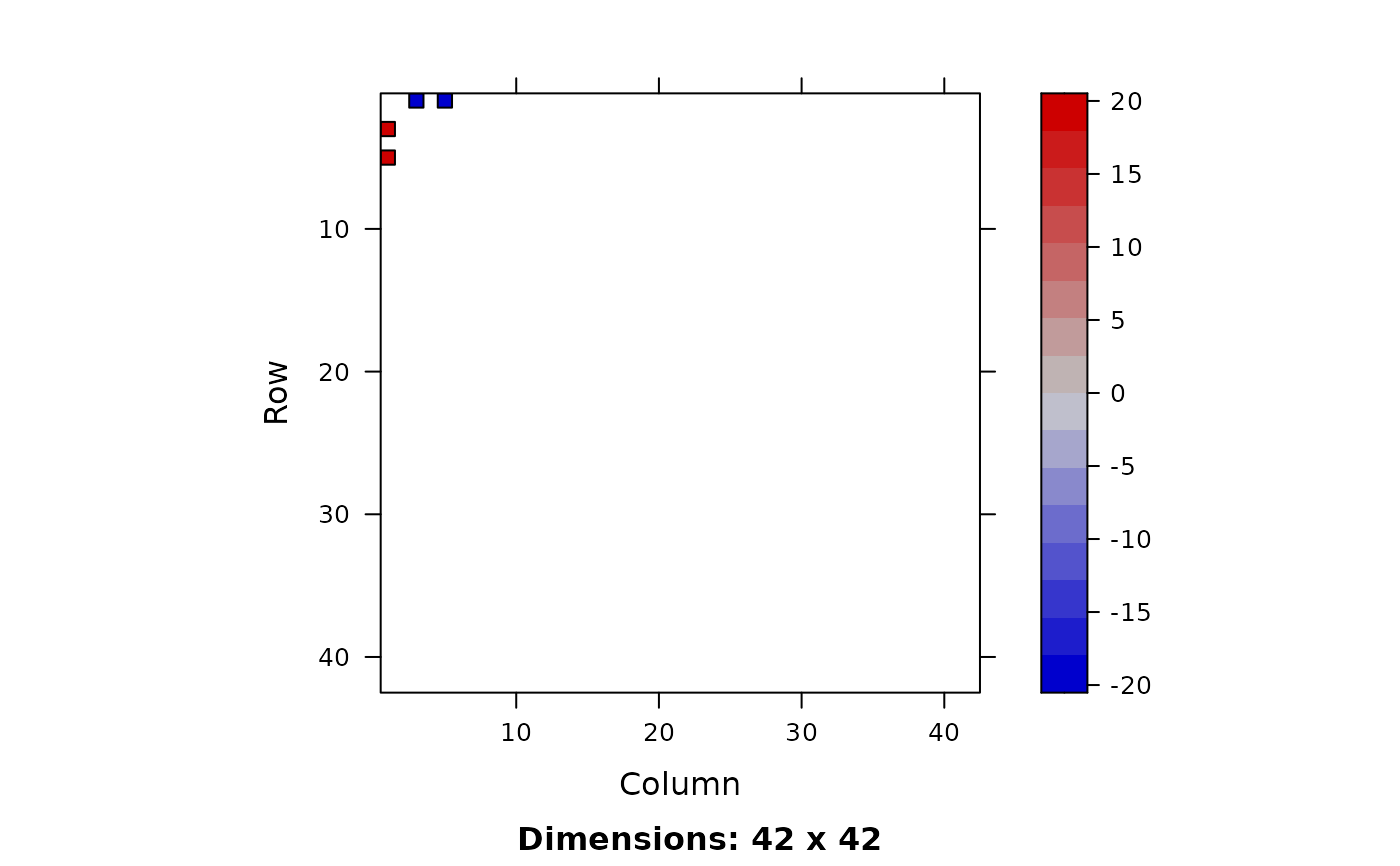
image(drop0(skewpart(a)))
isSymmetric(a) # FALSE
#> [1] FALSE
image(drop0(skewpart(a)))
 image(ia0 <- solve(a, tol = 0)) # checker board, dense [but really, a is singular!]
image(ia0 <- solve(a, tol = 0)) # checker board, dense [but really, a is singular!]
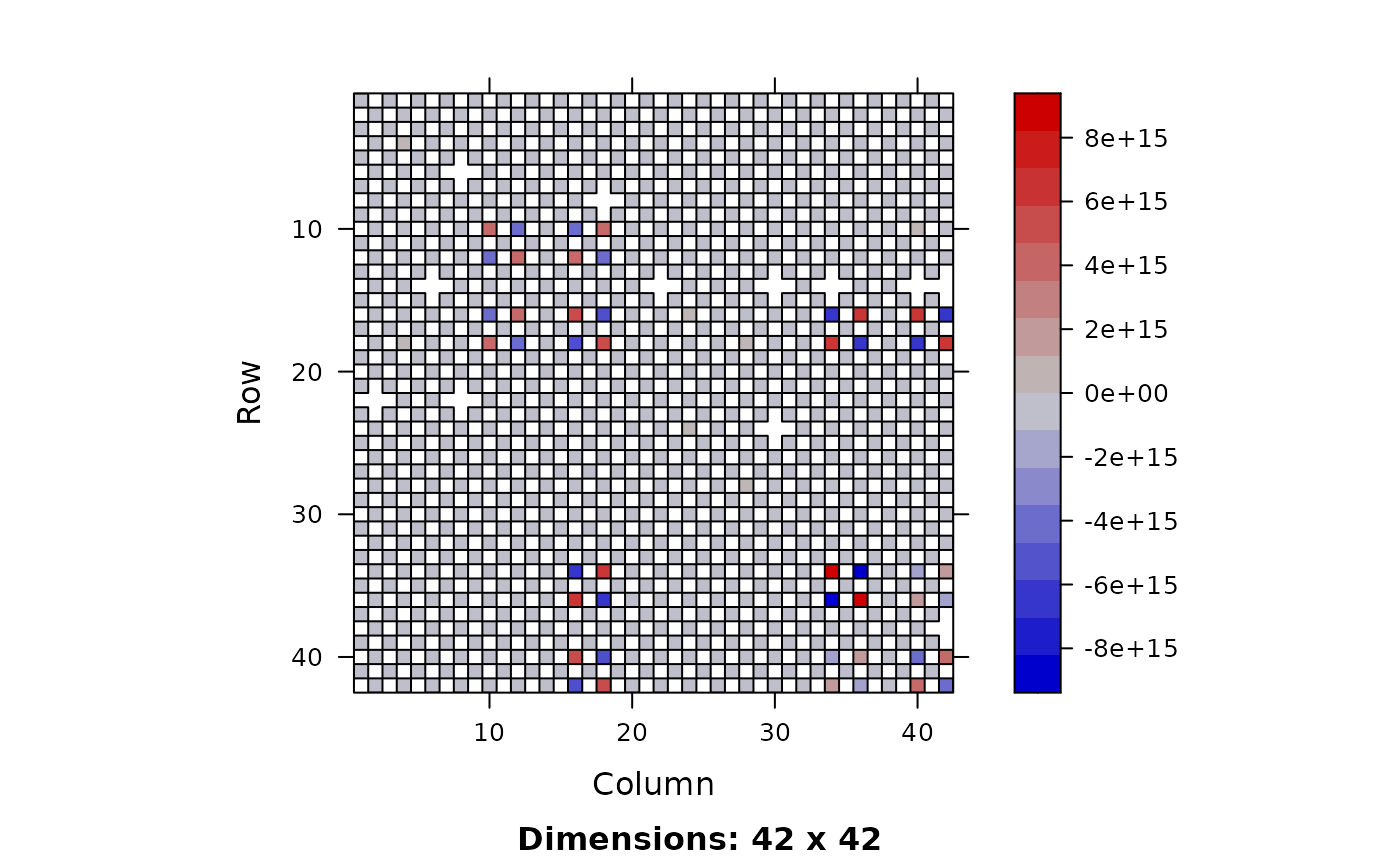 try(solve(a, sparse=TRUE))##-> error [ TODO: assertError ]
#> Error in .solve.checkCondBound(a@U, tol) :
#> 'a' is computationally singular, min(d)/max(d)=3.03577e-18, d=abs(diag(U))
ia. <- solve(a, sparse=TRUE, tol = 1e-19)##-> *no* error
if(R.version$arch == "x86_64")
## Fails on 32-bit [Fedora 19, R 3.0.2] from Matrix 1.1-0 on [FIXME ??] only
stopifnot(all.equal(as.matrix(ia.), as.matrix(ia0)))
a <- a + Diagonal(n)
iad <- solve(a)
ias <- solve(a, sparse=FALSE)
stopifnot(all.equal(as(iad,"denseMatrix"), ias, tolerance=1e-14))
I. <- iad %*% a ; image(I.)
try(solve(a, sparse=TRUE))##-> error [ TODO: assertError ]
#> Error in .solve.checkCondBound(a@U, tol) :
#> 'a' is computationally singular, min(d)/max(d)=3.03577e-18, d=abs(diag(U))
ia. <- solve(a, sparse=TRUE, tol = 1e-19)##-> *no* error
if(R.version$arch == "x86_64")
## Fails on 32-bit [Fedora 19, R 3.0.2] from Matrix 1.1-0 on [FIXME ??] only
stopifnot(all.equal(as.matrix(ia.), as.matrix(ia0)))
a <- a + Diagonal(n)
iad <- solve(a)
ias <- solve(a, sparse=FALSE)
stopifnot(all.equal(as(iad,"denseMatrix"), ias, tolerance=1e-14))
I. <- iad %*% a ; image(I.)
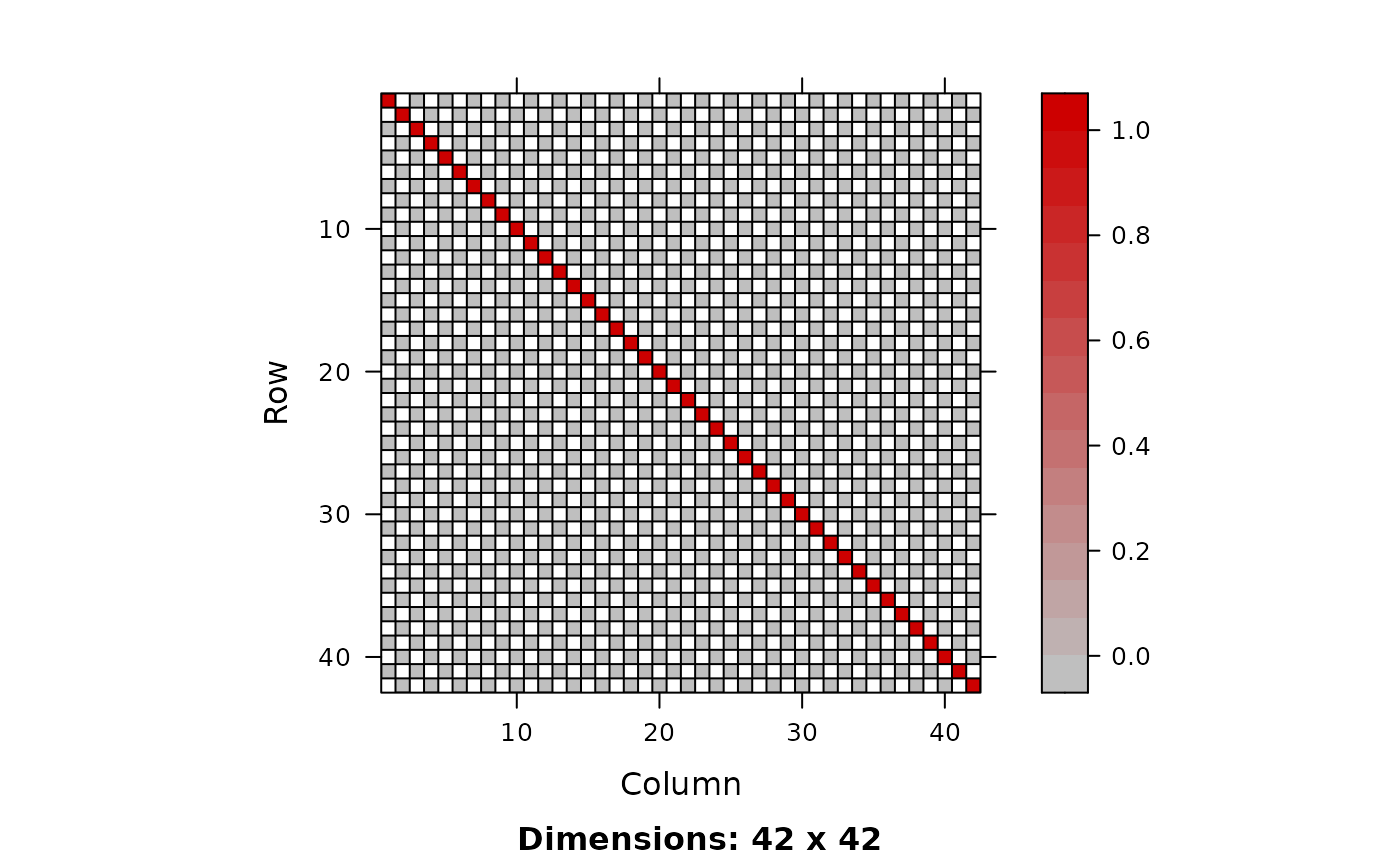 I0 <- drop0(zapsmall(I.)); image(I0)
I0 <- drop0(zapsmall(I.)); image(I0)
 .I <- a %*% iad
.I0 <- drop0(zapsmall(.I))
stopifnot( all.equal(as(I0, "diagonalMatrix"), Diagonal(n)),
all.equal(as(.I0,"diagonalMatrix"), Diagonal(n)) )
.I <- a %*% iad
.I0 <- drop0(zapsmall(.I))
stopifnot( all.equal(as(I0, "diagonalMatrix"), Diagonal(n)),
all.equal(as(.I0,"diagonalMatrix"), Diagonal(n)) )