Imputation by multivariate predictive mean matching

Imputes multivariate incomplete data among which there are specific relations, for instance, polynomials, interactions, range restrictions and sum scores.

mice.impute.mpmm(data, format = "imputes", ...)

Arguments

data: matrix with exactly two missing data patterns
format: A character vector specifying the type of object that should be returned. The default is format = "imputes".
...: Other named arguments.

Value

A matrix with imputed data, which has ncol(y) columns and sum(wy) rows.

Details

This function implements the predictive mean matching and applies canonical regression analysis to select donors fora set of missing variables. In general, canonical regressionanalysis looks for a linear combination of covariates that predicts a linear combination of outcomes (a set of missing variables) optimally in a least-square sense (Israels, 1987). The predicted value of the linear combination of the set of missing variables would be applied to perform predictive mean matching.

Note

The function requires variables in the block have the same missingness pattern. If there are more than one missingness pattern, the function will return a warning.

Other univariate imputation functions: mice.impute.cart(), mice.impute.lasso.logreg(), mice.impute.lasso.norm(), mice.impute.lasso.select.logreg(), mice.impute.lasso.select.norm(), mice.impute.lda(), mice.impute.logreg(), mice.impute.logreg.boot(), mice.impute.mean(), mice.impute.midastouch(), mice.impute.mnar.logreg(), mice.impute.norm(), mice.impute.norm.boot(), mice.impute.norm.nob(), mice.impute.norm.predict(), mice.impute.pmm(), mice.impute.polr(), mice.impute.polyreg(), mice.impute.quadratic(), mice.impute.rf(), mice.impute.ri()

Author

Mingyang Cai and Gerko Vink

Examples

# simulate data
beta2 <- beta1 <- .5
x <- rnorm(1000)
e <- rnorm(1000, 0, 1)
y <- beta1 * x + beta2 * x^2 + e
dat <- data.frame(y = y, x = x, x2 = x^2)
m <- as.logical(rbinom(1000, 1, 0.25))
dat[m, c("x", "x2")] <- NA

# impute
blk <- list("y", c("x", "x2"))
meth <- c("", "mpmm")
imp <- mice(dat, blocks = blk, method = meth, print = FALSE,
    m = 2, maxit = 2)

# analyse and check
summary(pool(with(imp, lm(y ~ x + x2))))
#>          term   estimate  std.error  statistic        df      p.value
#> 1 (Intercept) 0.03113943 0.04146686  0.7509473 38.589154 4.572395e-01
#> 2           x 0.50054117 0.03501063 14.2968326 37.065309 1.162119e-16
#> 3          x2 0.48960396 0.03097395 15.8069581  5.635635 6.971423e-06
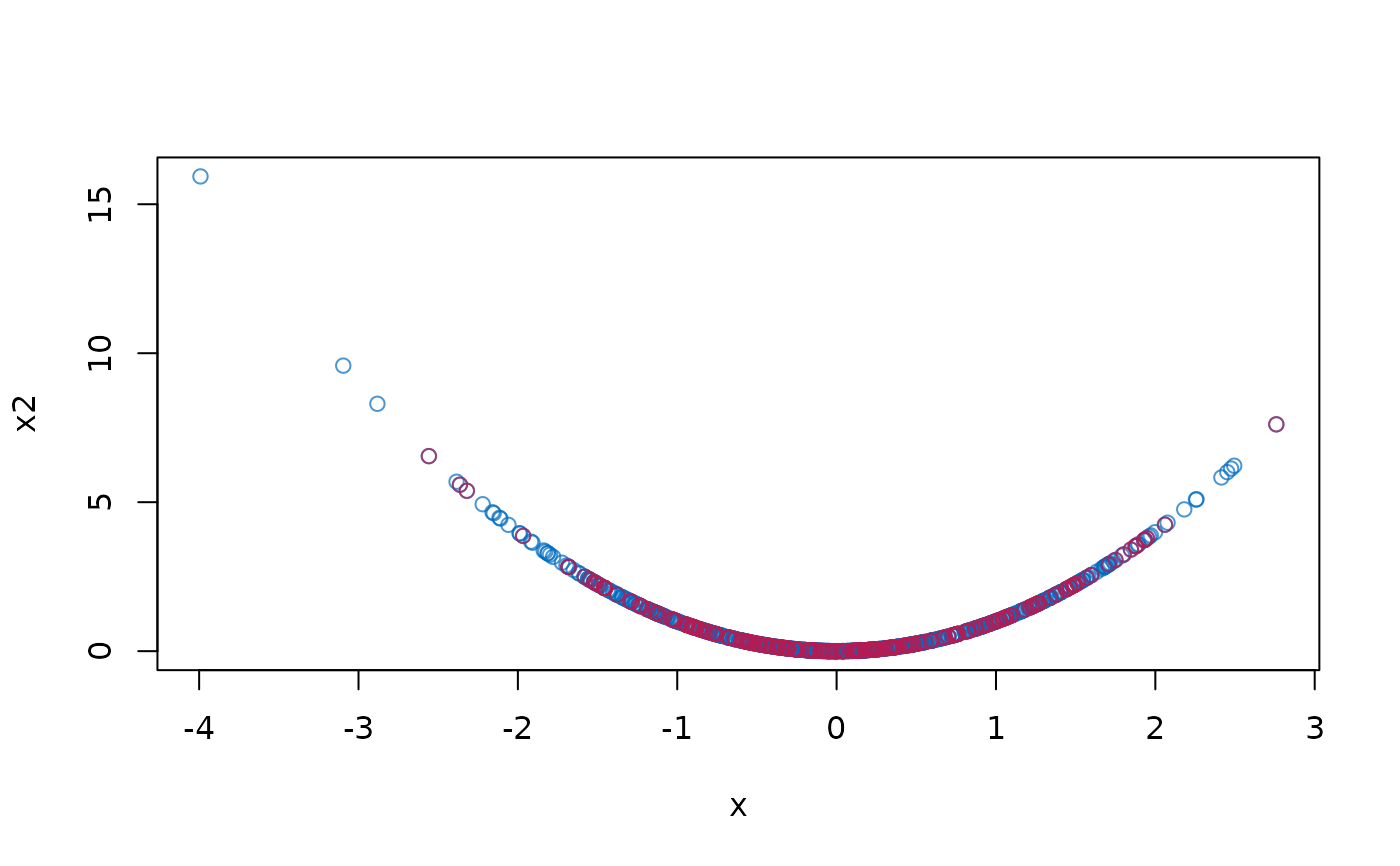
with(dat, plot(x, x2, col = mdc(1)))
with(complete(imp), points(x[m], x2[m], col = mdc(2)))