Imputation by predictive mean matching
mice.impute.pmm(
y,
ry,
x,
wy = NULL,
donors = 5L,
matchtype = 1L,
exclude = NULL,
quantify = TRUE,
trim = 1L,
ridge = 1e-05,
use.matcher = FALSE,
...
)Arguments
- y
Vector to be imputed
- ry
Logical vector of length
length(y)indicating the the subsety[ry]of elements inyto which the imputation model is fitted. Therygenerally distinguishes the observed (TRUE) and missing values (FALSE) iny.- x
Numeric design matrix with
length(y)rows with predictors fory. Matrixxmay have no missing values.- wy
Logical vector of length
length(y). ATRUEvalue indicates locations inyfor which imputations are created.- donors
The size of the donor pool among which a draw is made. The default is
donors = 5L. Settingdonors = 1Lalways selects the closest match, but is not recommended. Values between 3L and 10L provide the best results in most cases (Morris et al, 2015).- matchtype
Type of matching distance. The default choice (
matchtype = 1L) calculates the distance between the predicted value ofyobsand the drawn values ofymis(called type-1 matching). Other choices arematchtype = 0L(distance between predicted values) andmatchtype = 2L(distance between drawn values).- exclude
Dependent values to exclude from the imputation model and the collection of donor values
- quantify
Logical. If
TRUE, factor levels are replaced by the first canonical variate before fitting the imputation model. If false, the procedure reverts to the old behaviour and takes the integer codes (which may lack a sensible interpretation). Relevant only ofyis a factor.- trim
Scalar integer. Minimum number of observations required in a category in order to be considered as a potential donor value. Relevant only of
yis a factor.- ridge
The ridge penalty used in
.norm.draw()to prevent problems with multicollinearity. The default isridge = 1e-05, which means that 0.01 percent of the diagonal is added to the cross-product. Larger ridges may result in more biased estimates. For highly noisy data (e.g. many junk variables), setridge = 1e-06or even lower to reduce bias. For highly collinear data, setridge = 1e-04or higher.- use.matcher
Logical. Set
use.matcher = TRUEto specify the C functionmatcher(), the now deprecated matching function that was default in versions2.22(June 2014) to3.11.7(Oct 2020). Since version3.12.0mice()uses the much fastermatchindexC function. Use the deprecatedmatcherfunction only for exact reproduction.- ...
Other named arguments.
Value
Vector with imputed data, same type as y, and of length
sum(wy)
Details
Imputation of y by predictive mean matching, based on
van Buuren (2012, p. 73). The procedure is as follows:
Calculate the cross-product matrix \(S=X_{obs}'X_{obs}\).
Calculate \(V = (S+{diag}(S)\kappa)^{-1}\), with some small ridge parameter \(\kappa\).
Calculate regression weights \(\hat\beta = VX_{obs}'y_{obs}.\)
Draw \(q\) independent \(N(0,1)\) variates in vector \(\dot z_1\).
Calculate \(V^{1/2}\) by Cholesky decomposition.
Calculate \(\dot\beta = \hat\beta + \dot\sigma\dot z_1 V^{1/2}\).
Calculate \(\dot\eta(i,j)=|X_{{obs},[i]|}\hat\beta-X_{{mis},[j]}\dot\beta\) with \(i=1,\dots,n_1\) and \(j=1,\dots,n_0\).
Construct \(n_0\) sets \(Z_j\), each containing \(d\) candidate donors, from \(y_{obs}\) such that \(\sum_d\dot\eta(i,j)\) is minimum for all \(j=1,\dots,n_0\). Break ties randomly.
Draw one donor \(i_j\) from \(Z_j\) randomly for \(j=1,\dots,n_0\).
Calculate imputations \(\dot y_j = y_{i_j}\) for \(j=1,\dots,n_0\).
The name predictive mean matching was proposed by Little (1988).
References
Little, R.J.A. (1988), Missing data adjustments in large surveys (with discussion), Journal of Business Economics and Statistics, 6, 287–301.
Morris TP, White IR, Royston P (2015). Tuning multiple imputation by predictive mean matching and local residual draws. BMC Med Res Methodol. ;14:75.
Van Buuren, S. (2018). Flexible Imputation of Missing Data. Second Edition. Chapman & Hall/CRC. Boca Raton, FL.
Van Buuren, S., Groothuis-Oudshoorn, K. (2011). mice: Multivariate
Imputation by Chained Equations in R. Journal of Statistical
Software, 45(3), 1-67. doi:10.18637/jss.v045.i03
See also
Other univariate imputation functions:
mice.impute.cart(),
mice.impute.lasso.logreg(),
mice.impute.lasso.norm(),
mice.impute.lasso.select.logreg(),
mice.impute.lasso.select.norm(),
mice.impute.lda(),
mice.impute.logreg(),
mice.impute.logreg.boot(),
mice.impute.mean(),
mice.impute.midastouch(),
mice.impute.mnar.logreg(),
mice.impute.mpmm(),
mice.impute.norm(),
mice.impute.norm.boot(),
mice.impute.norm.nob(),
mice.impute.norm.predict(),
mice.impute.polr(),
mice.impute.polyreg(),
mice.impute.quadratic(),
mice.impute.rf(),
mice.impute.ri()
Examples
# We normally call mice.impute.pmm() from within mice()
# But we may call it directly as follows (not recommended)
set.seed(53177)
xname <- c("age", "hgt", "wgt")
r <- stats::complete.cases(boys[, xname])
x <- boys[r, xname]
y <- boys[r, "tv"]
ry <- !is.na(y)
table(ry)
#> ry
#> FALSE TRUE
#> 503 224
# percentage of missing data in tv
sum(!ry) / length(ry)
#> [1] 0.6918845
# Impute missing tv data
yimp <- mice.impute.pmm(y, ry, x)
length(yimp)
#> [1] 503
hist(yimp, xlab = "Imputed missing tv")
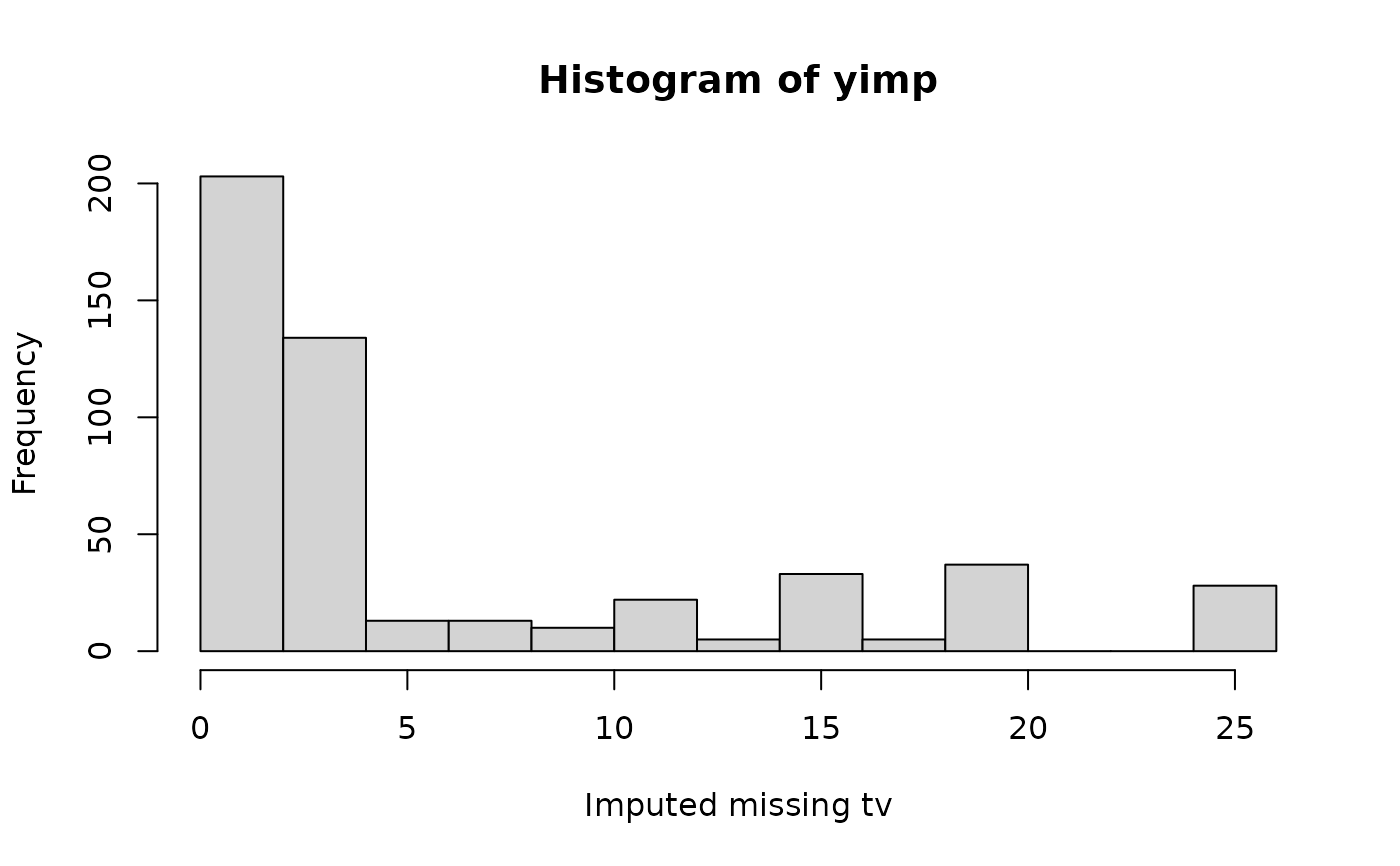 # Impute all tv data
yimp <- mice.impute.pmm(y, ry, x, wy = rep(TRUE, length(y)))
length(yimp)
#> [1] 727
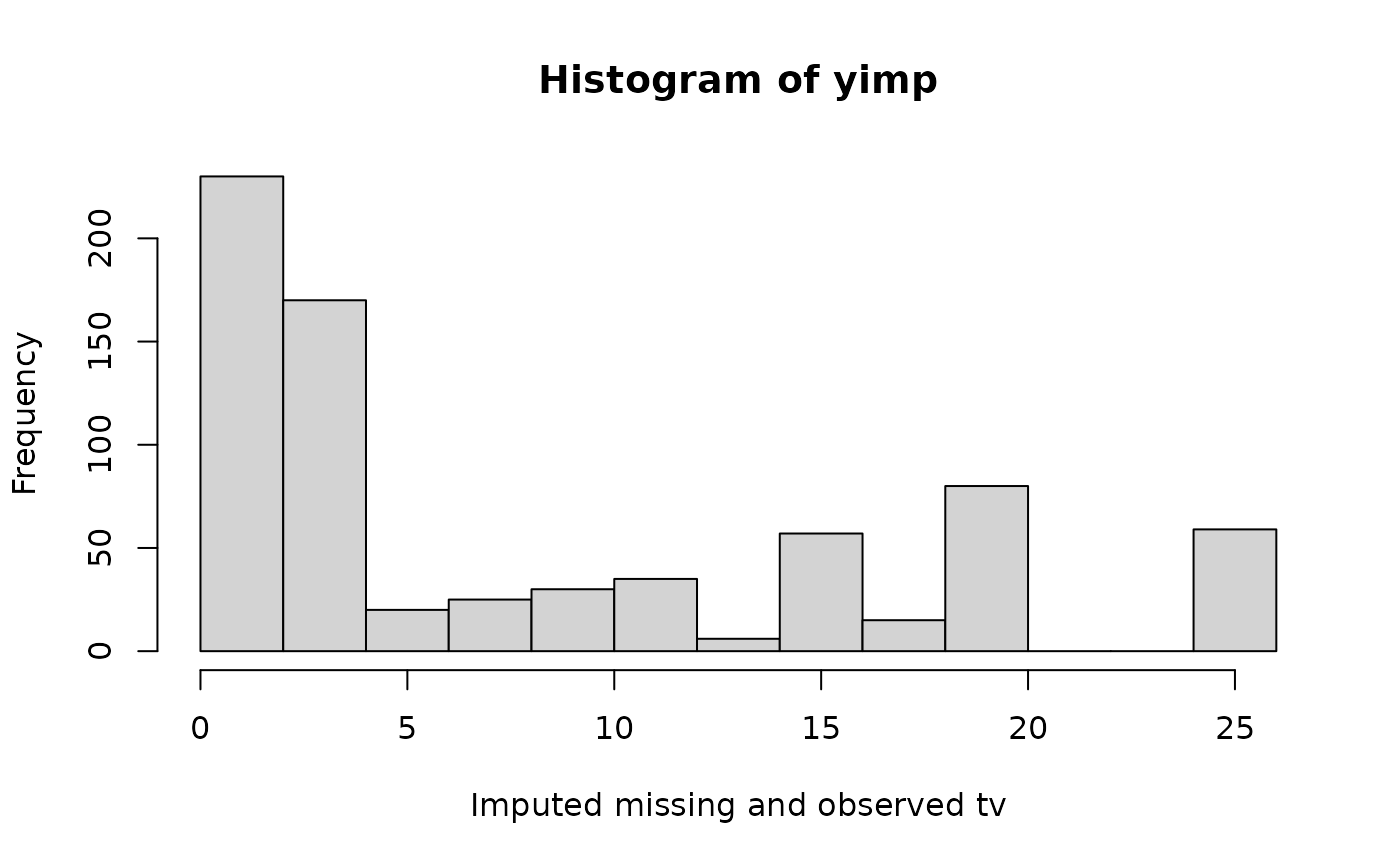
hist(yimp, xlab = "Imputed missing and observed tv")
# Impute all tv data
yimp <- mice.impute.pmm(y, ry, x, wy = rep(TRUE, length(y)))
length(yimp)
#> [1] 727
hist(yimp, xlab = "Imputed missing and observed tv")
 plot(jitter(y), jitter(yimp),
main = "Predictive mean matching on age, height and weight",
xlab = "Observed tv (n = 224)",
ylab = "Imputed tv (n = 224)"
)
abline(0, 1)
plot(jitter(y), jitter(yimp),
main = "Predictive mean matching on age, height and weight",
xlab = "Observed tv (n = 224)",
ylab = "Imputed tv (n = 224)"
)
abline(0, 1)
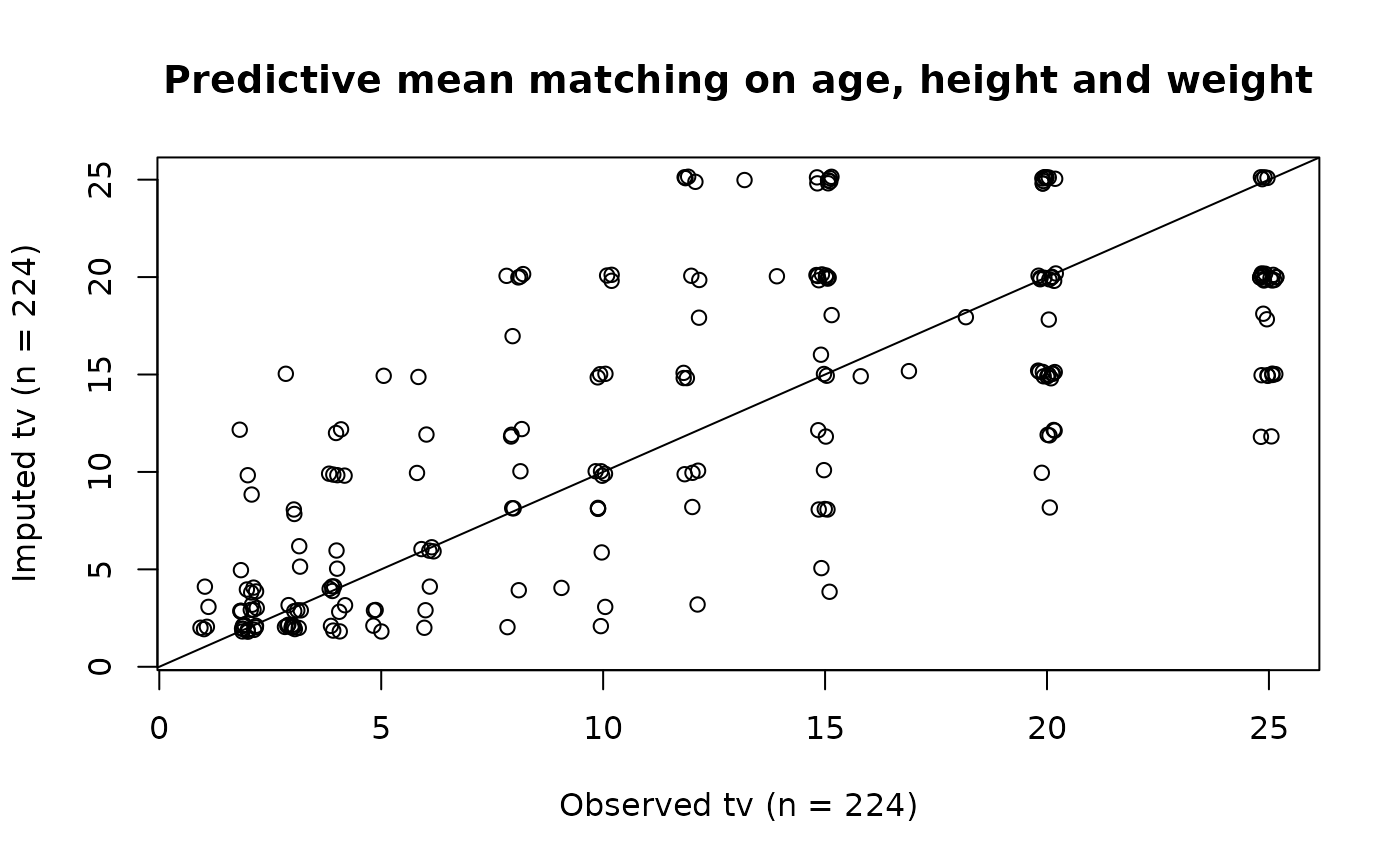 cor(y, yimp, use = "pair")
#> [1] 0.7415001
# Use blots to exclude different values per column
# Create blots object
blots <- make.blots(boys)
# Exclude ml 1 through 5 from tv donor pool
blots$tv$exclude <- c(1:5)
# Exclude 100 random observed heights from tv donor pool
blots$hgt$exclude <- sample(unique(boys$hgt), 100)
imp <- mice(boys, method = "pmm", print = FALSE, blots = blots, seed=123)
#> Error in chol.default(sym(p$v)): the leading minor of order 4 is not positive
blots$hgt$exclude %in% unlist(c(imp$imp$hgt)) # MUST be all FALSE
#> Error: object 'imp' not found
blots$tv$exclude %in% unlist(c(imp$imp$tv)) # MUST be all FALSE
#> Error: object 'imp' not found
# Factor quantification
xname <- c("age", "hgt", "wgt")
br <- boys[c(1:10, 101:110, 501:510, 601:620, 701:710), ]
r <- stats::complete.cases(br[, xname])
x <- br[r, xname]
y <- factor(br[r, "tv"])
ry <- !is.na(y)
table(y)
#> y
#> 6 8 10 12 13 15 16 20 25
#> 1 2 1 1 1 4 1 4 7
# impute factor by optimizing canonical correlation y, x
mice.impute.pmm(y, ry, x)
#> [1] 25 12 25 25 25 20 25 12 20 25 20 25 25 25 25 20 25 25 20 25 20 15 13 25 15
#> [26] 15 15 10 25 8 8 25 25 15 15 15 10 25
#> Levels: 6 8 10 12 13 15 16 20 25
# only categories with at least 2 cases can be donor
mice.impute.pmm(y, ry, x, trim = 2L)
#> [1] 8 20 8 8 20 8 15 20 25 8 15 15 20 8 15 8 15 8 8 15 20 15 8 15 20
#> [26] 20 25 15 15 25 20 25 25 15 25 25 15 25
#> Levels: 6 8 10 12 13 15 16 20 25
# in addition, eliminate category 20
mice.impute.pmm(y, ry, x, trim = 2L, exclude = 20)
#> [1] 8 25 8 25 25 8 25 25 8 25 15 15 8 15 8 8 25 8 8 25 15 15 25 25 25
#> [26] 25 25 25 25 25 8 25 15 25 15 15 25 25
#> Levels: 6 8 10 12 13 15 16 20 25
# to get old behavior: as.integer(y))
mice.impute.pmm(y, ry, x, quantify = FALSE)
#> [1] 12 15 6 10 10 12 12 8 8 6 8 10 15 15 12 12 8 8 6 8 12 8 6 15 20
#> [26] 20 6 15 20 15 20 13 12 25 15 25 25 20
#> Levels: 6 8 10 12 13 15 16 20 25
cor(y, yimp, use = "pair")
#> [1] 0.7415001
# Use blots to exclude different values per column
# Create blots object
blots <- make.blots(boys)
# Exclude ml 1 through 5 from tv donor pool
blots$tv$exclude <- c(1:5)
# Exclude 100 random observed heights from tv donor pool
blots$hgt$exclude <- sample(unique(boys$hgt), 100)
imp <- mice(boys, method = "pmm", print = FALSE, blots = blots, seed=123)
#> Error in chol.default(sym(p$v)): the leading minor of order 4 is not positive
blots$hgt$exclude %in% unlist(c(imp$imp$hgt)) # MUST be all FALSE
#> Error: object 'imp' not found
blots$tv$exclude %in% unlist(c(imp$imp$tv)) # MUST be all FALSE
#> Error: object 'imp' not found
# Factor quantification
xname <- c("age", "hgt", "wgt")
br <- boys[c(1:10, 101:110, 501:510, 601:620, 701:710), ]
r <- stats::complete.cases(br[, xname])
x <- br[r, xname]
y <- factor(br[r, "tv"])
ry <- !is.na(y)
table(y)
#> y
#> 6 8 10 12 13 15 16 20 25
#> 1 2 1 1 1 4 1 4 7
# impute factor by optimizing canonical correlation y, x
mice.impute.pmm(y, ry, x)
#> [1] 25 12 25 25 25 20 25 12 20 25 20 25 25 25 25 20 25 25 20 25 20 15 13 25 15
#> [26] 15 15 10 25 8 8 25 25 15 15 15 10 25
#> Levels: 6 8 10 12 13 15 16 20 25
# only categories with at least 2 cases can be donor
mice.impute.pmm(y, ry, x, trim = 2L)
#> [1] 8 20 8 8 20 8 15 20 25 8 15 15 20 8 15 8 15 8 8 15 20 15 8 15 20
#> [26] 20 25 15 15 25 20 25 25 15 25 25 15 25
#> Levels: 6 8 10 12 13 15 16 20 25
# in addition, eliminate category 20
mice.impute.pmm(y, ry, x, trim = 2L, exclude = 20)
#> [1] 8 25 8 25 25 8 25 25 8 25 15 15 8 15 8 8 25 8 8 25 15 15 25 25 25
#> [26] 25 25 25 25 25 8 25 15 25 15 15 25 25
#> Levels: 6 8 10 12 13 15 16 20 25
# to get old behavior: as.integer(y))
mice.impute.pmm(y, ry, x, quantify = FALSE)
#> [1] 12 15 6 10 10 12 12 8 8 6 8 10 15 15 12 12 8 8 6 8 12 8 6 15 20
#> [26] 20 6 15 20 15 20 13 12 25 15 25 25 20
#> Levels: 6 8 10 12 13 15 16 20 25