Huberization – Bringing Outliers In

Huberization (named after Peter Huber's M-estimation algorithm for location originally) replaces outlying values in a sample x by their respective boundary: when \(x_j < c_1\) it is replaced by \(c_1\) and when \(x_j > c_2\) it is replaced by \(c_2\). Consequently, values inside the interval \([c_1, c_2]\) remain unchanged.

Here, \(c_j = M \pm c\cdot s\) where \(s := s(x)\) is the robust scale estimate Qn(x) if that is positive, and by default, \(M\) is the robust huber estimate of location \(\mu\) (with tuning constant \(k\)).

In the degenerate case where Qn(x) == 0, trimmed means of abs(x - M) are tried as scale estimate \(s\), with decreasing trimming proportions specified by the decreasing trim vector.

huberize(x, M = huberM(x, k = k)$mu, c = k,
         trim = (5:1)/16,
         k = 1.5,
         warn0 = getOption("verbose"), saveTrim = TRUE)

Arguments

x

numeric vector which is to be huberized.

M

a number; defaulting to huberM(x, k), the robust Huber M-estimator of location.

c

a positive number, the tuning constant for huberization of the sample x.

trim

a decreasing vector of trimming proportions in \([0, 0.5]\), only used to trim the absolute deviations from M in case Qn(x) is zero.

k

used if M is not specified as huberization center M, and so, by default is taken as Huber's M-estimate huberM(x, k).

warn0

logical indicating if a warning should be signalled in case Qn(x) is zero and the trimmed means for all trimming proportions trim are zero as well.

saveTrim

a logical indicating if the last tried trim[j] value should be stored if Qn(x) was zero.

Details

  • In regular cases, s = Qn(x) is positive and used to huberize values of x outside [M - c*s, M + c*s].

  • In degenerate cases where Qn(x) == 0, we search for an \(s > 0\) by trying the trimmed mean s := mean(abs(x-M), trim = trim[j]) with less and less trimming (as the trimming proportions trim[] must decrease). If even the last, trim[length(trim)], leads to \(s = 0\), a warning is printed when warn0 is true.

Value

a numeric vector as x; in case Qn(x) was zero and saveTrim is true, also containing the (last) trim proportion used (to compute the scale \(s\)) as attribute "trim" (see attr(), attributes).

Author

Martin Maechler

Note

For the use in mc() and similar cases where mainly numerical stabilization is necessary, a large c = 1e12 will lead to no huberization, i.e., all y == x for y <- huberize(x, c) for typical non-degenerate samples.

See also

huberM and mc which is now stabilized by default via something like huberize(*, c=1e11).

Examples

## For non-degenerate data and large c, nothing is huberized,
## as there are *no* really extreme outliers :
set.seed(101)
x <- rnorm(1000)
stopifnot(all.equal(x, huberize(x, c=100)))
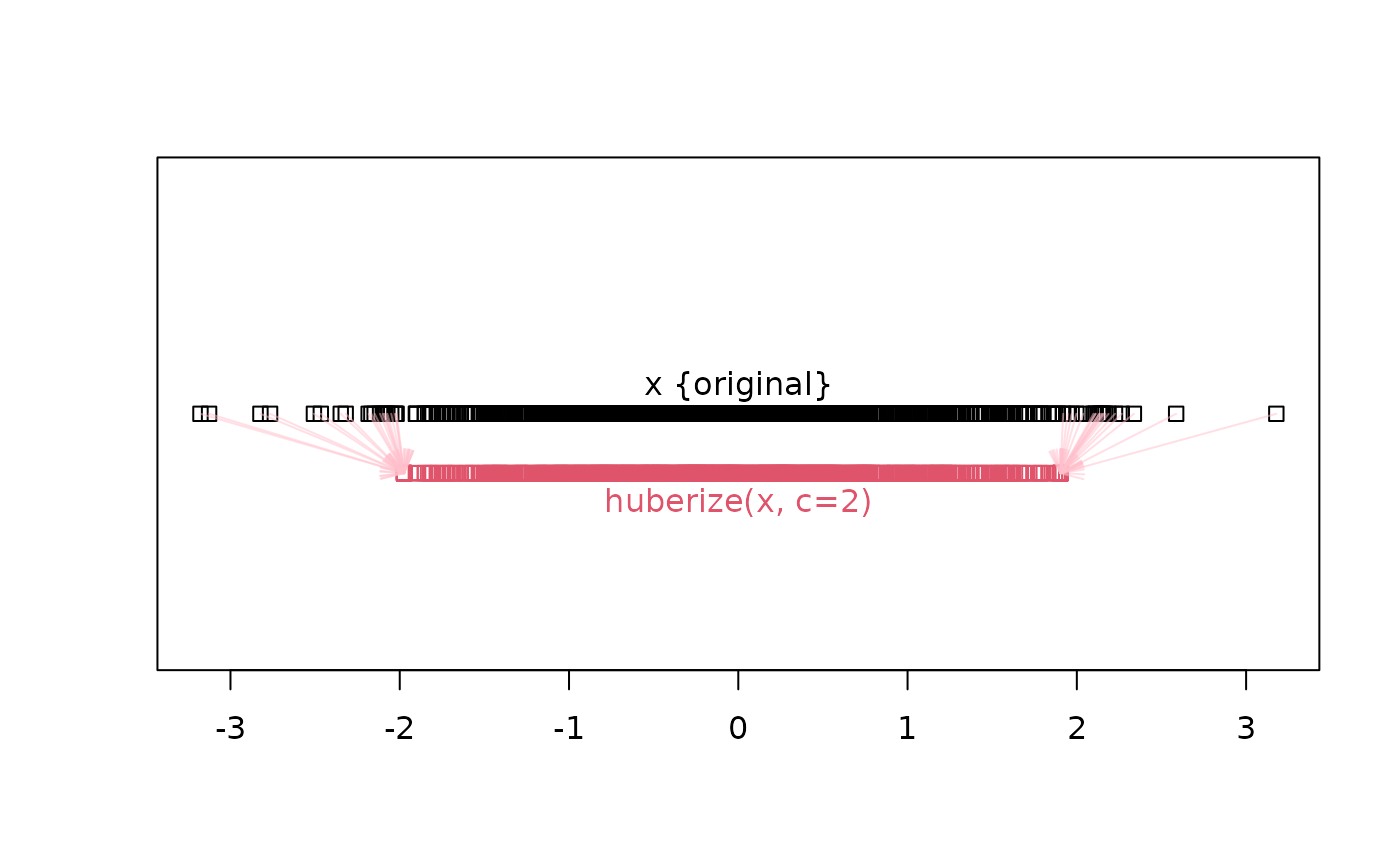
## OTOH, the "extremes" are shrunken towards the boundaries for smaller c:
xh <- huberize(x, c = 2)
table(x != xh)
#> 
#> FALSE  TRUE 
#>   960    40 
## 45 out of a 1000:
table(xh[x != xh])# 26 on the left boundary -2.098 and 19 on the right = 2.081
#> 
#> -1.97404853359006  1.90241504050778 
#>                20                20 
## vizualization:
stripchart(x); text(0,1, "x {original}", pos=3); yh <- 0.9
stripchart(xh, at = yh, add=TRUE, col=2)
text(0, yh, "huberize(x, c=2)",   col=2, pos=1)
arrows( x[x!=xh], 1,
       xh[x!=xh], yh, length=1/8, col=adjustcolor("pink", 1/2))