Stahel's Residual Plot against 2 X's
p.res.2x.RdPlot Residuals, e.g., of a multiple linear regression, against two (predictor) variables, using positively and negatively oriented line segments for positive and negative residuals.
This is a (S3) generic function with a default and a
formula method.
Usage
p.res.2x(x, ...)
# Default S3 method
p.res.2x(x, y, z, restricted, size = 1, slwd = 1, scol = 2:3,
xlab = NULL, ylab = NULL, main = NULL,
xlim = range(x), ylim = range(y), ...)
# S3 method for class 'formula'
p.res.2x(x = ~., data, main = deparse(substitute(data)),
xlab = NULL, ylab = NULL, ...)Arguments
- x, y
numeric vectors of the same length specifying 2 covariates. For the
formulamethod,xis aformula.- z
numeric vector of same length as
xandy, typically residuals.- restricted
positive value which truncates the size. The corresponding symbols are marked by stars.
- size
the symbols are scaled so that
sizeis the size of the largest symbol in cm.- slwd, scol
line width and color(s) for the residual
segments. Ifscolhas length 2 as per default, the two colors are used for positive and negativezvalues, respectively.- xlab, ylab, main
axis labels, and title see
title, each with a sensible default. To suppress, use, e.g.,main = "".- xlim, ylim
the basic x- and y- axis extents, see
plot.default. Note that these will be slightly extended such that segments are not cut off.- ...
further arguments passed to
plot, orp.res.2x.default(), respectively.- data
(for the
formulamethod:) a data frame or a fitted"lm"object.
Details
Each residual zz[i] is visualized as line segment centered at
\((xx_i,yy_i)\), \(i=1,\dots,n\), where the
lengths of the segments are proportional to the absolute
values \(\|zz_i\|\).
Positive residuals' line segments have slope \(+1\), and negative ones
slope \(-1\), and scol is used to use different colors for
negative and positive segments.
The formula interface calls p.res.2fact() when
both x and y are factors.
References
Stahel, W.~A. (2008) Statistische Datenanalyse: Eine Einführung für Naturwissenschaftler, 5. Auflage, Vieweg, Wiesbaden; Paragraph 13.8.r and 13.8.v.
Examples
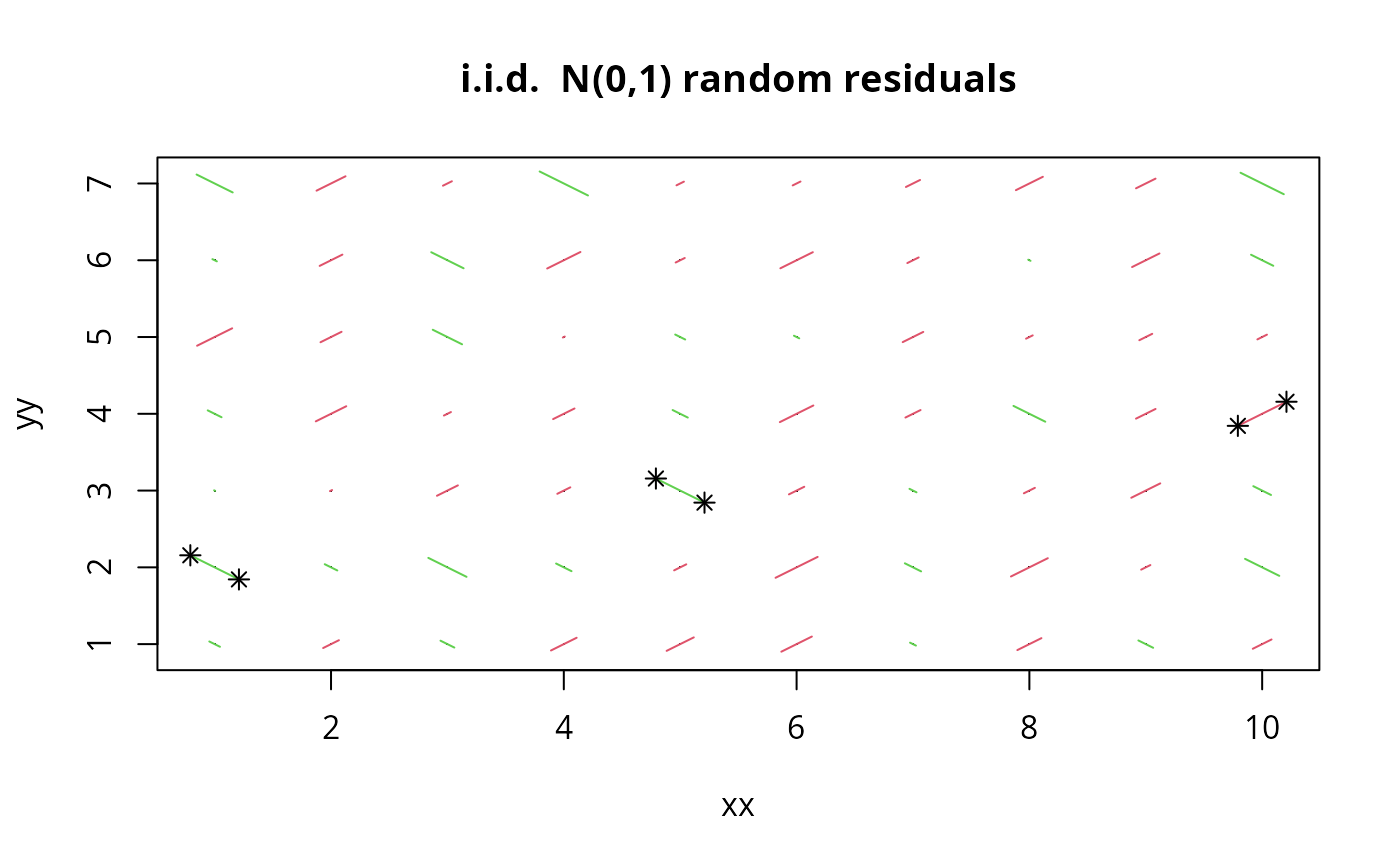
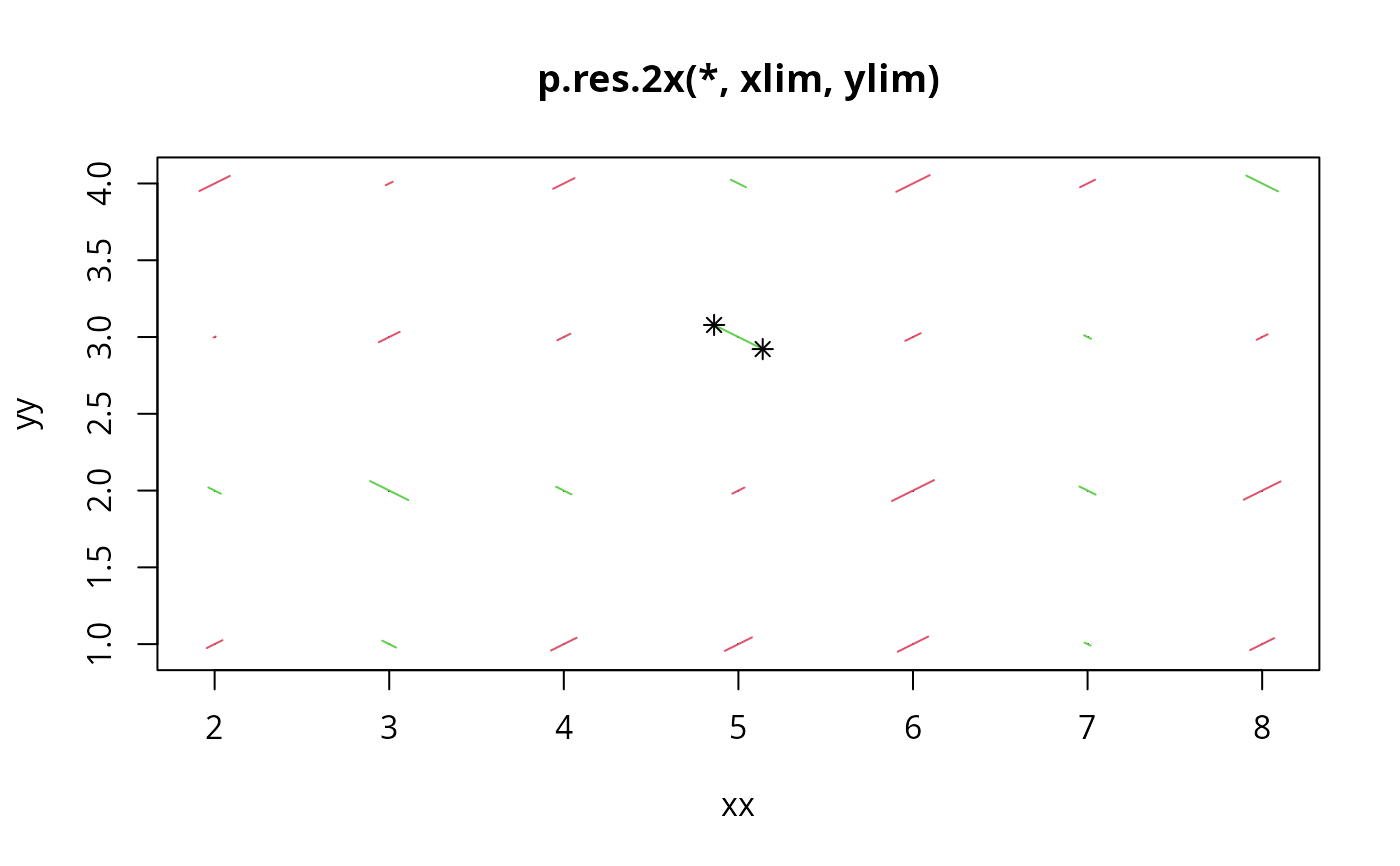
xx <- rep(1:10,7)
yy <- rep(1:7, rep(10,7))
zz <- rnorm(70)
p.res.2x(xx,yy,zz, restricted = 2, main = "i.i.d. N(0,1) random residuals")
 example(lm.influence, echo = FALSE)
#> List of 4
#> $ hat : Named num [1:50] 0.0677 0.1204 0.0875 0.0895 0.0696 ...
#> ..- attr(*, "names")= chr [1:50] "Australia" "Austria" "Belgium" "Bolivia" ...
#> $ coefficients: num [1:50, 1:5] 0.0916 -0.0747 -0.4752 0.0429 0.6604 ...
#> ..- attr(*, "dimnames")=List of 2
#> .. ..$ : chr [1:50] "Australia" "Austria" "Belgium" "Bolivia" ...
#> .. ..$ : chr [1:5] "(Intercept)" "pop15" "pop75" "dpi" ...
#> $ sigma : Named num [1:50] 3.84 3.84 3.83 3.84 3.81 ...
#> ..- attr(*, "names")= chr [1:50] "Australia" "Austria" "Belgium" "Bolivia" ...
#> $ wt.res : Named num [1:50] 0.864 0.616 2.219 -0.698 3.553 ...
#> ..- attr(*, "names")= chr [1:50] "Australia" "Austria" "Belgium" "Bolivia" ...
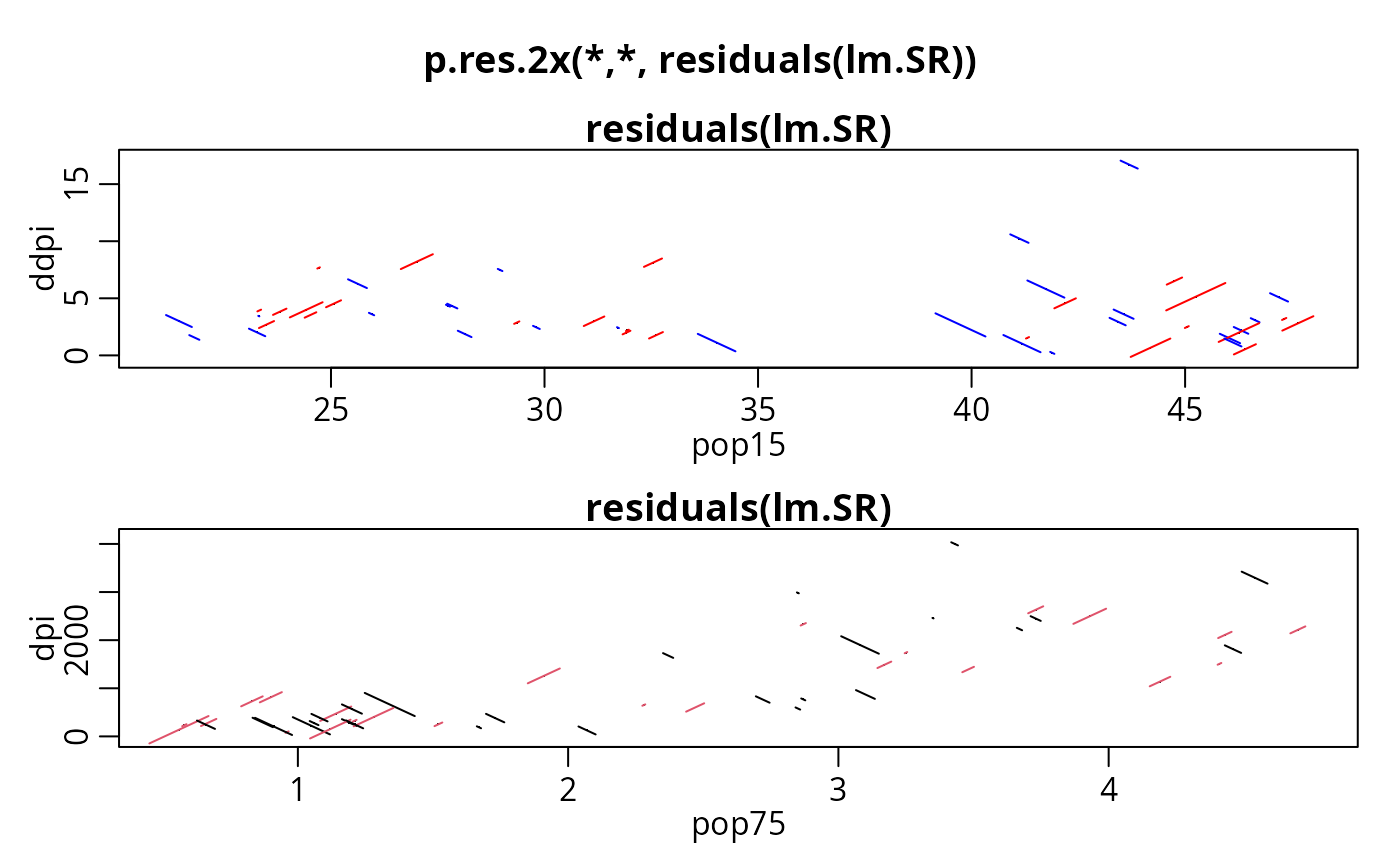
op <- mult.fig(2, marP=c(-1,-1,-1,0), main="p.res.2x(*,*, residuals(lm.SR))")$old.par
with(LifeCycleSavings,
{ p.res.2x(pop15, ddpi, residuals(lm.SR), scol=c("red", "blue"))
p.res.2x(pop75, dpi, residuals(lm.SR), scol=2:1)
})
example(lm.influence, echo = FALSE)
#> List of 4
#> $ hat : Named num [1:50] 0.0677 0.1204 0.0875 0.0895 0.0696 ...
#> ..- attr(*, "names")= chr [1:50] "Australia" "Austria" "Belgium" "Bolivia" ...
#> $ coefficients: num [1:50, 1:5] 0.0916 -0.0747 -0.4752 0.0429 0.6604 ...
#> ..- attr(*, "dimnames")=List of 2
#> .. ..$ : chr [1:50] "Australia" "Austria" "Belgium" "Bolivia" ...
#> .. ..$ : chr [1:5] "(Intercept)" "pop15" "pop75" "dpi" ...
#> $ sigma : Named num [1:50] 3.84 3.84 3.83 3.84 3.81 ...
#> ..- attr(*, "names")= chr [1:50] "Australia" "Austria" "Belgium" "Bolivia" ...
#> $ wt.res : Named num [1:50] 0.864 0.616 2.219 -0.698 3.553 ...
#> ..- attr(*, "names")= chr [1:50] "Australia" "Austria" "Belgium" "Bolivia" ...
op <- mult.fig(2, marP=c(-1,-1,-1,0), main="p.res.2x(*,*, residuals(lm.SR))")$old.par
with(LifeCycleSavings,
{ p.res.2x(pop15, ddpi, residuals(lm.SR), scol=c("red", "blue"))
p.res.2x(pop75, dpi, residuals(lm.SR), scol=2:1)
})
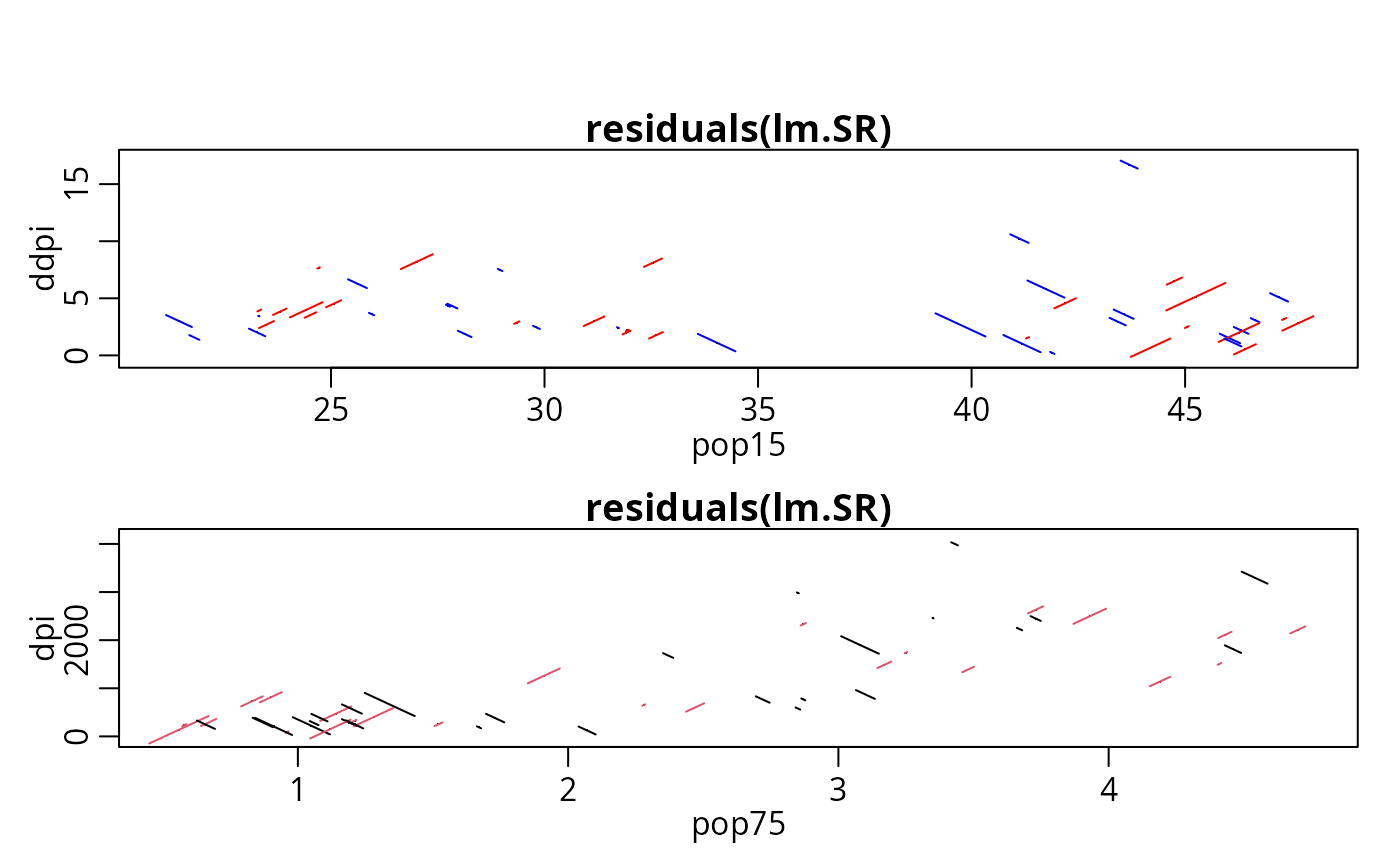
 ## with formula interface:
p.res.2x(~ pop15 + ddpi, lm.SR, scol=c("red", "blue"))
p.res.2x(~ pop75 + dpi, lm.SR, scol=2:1)
## with formula interface:
p.res.2x(~ pop15 + ddpi, lm.SR, scol=c("red", "blue"))
p.res.2x(~ pop75 + dpi, lm.SR, scol=2:1)
 par(op) # revert par() settings above
par(op) # revert par() settings above